【AI学习笔记3】神经元、神经网络与感知机 Neuron、Neural Network and Perceptron

神经元、神经网络与感知机 Neuron、Neural Network and Perceptron

 

一、从生物神经元到人工神经网络

        每个神经元细胞都向外伸出许多分支，其中用来接收输入的分支称作树突(dendrites)，用来输出信号的分支称作轴突(axon)，轴突连接到树突上形成一个突触(synapse)。每个神经元可以通过这种方式连接多个其他神经元，每个神经元也可以接受多个其他神经元的连接，很多连接起来的神经元形成了网状结构。【1】

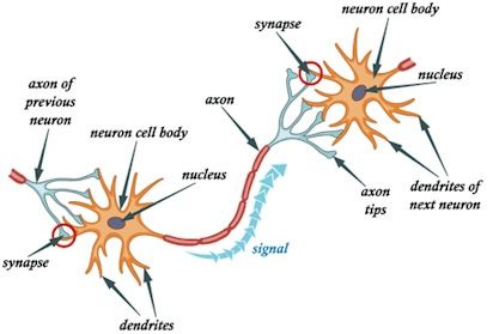
神经系统的信息传递，是通过神经信号来实现的。这些信号基于一个个神经元组成的神经纤维，进行远距离传递。 神经信号有两种：【2】

• 单个神经元内：电信号传递
• 神经元与神经元之间：化学信号传递（化学信号就是指通过释放化学物质及接收化学物质，来交换信息内容）

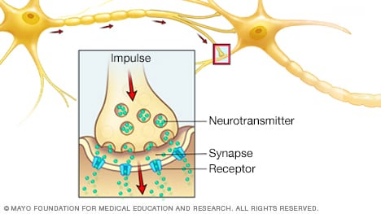
神经递质（neurotransmitter）【3】

当神经细胞受到刺激时，神经细胞便会通过电脉冲与其他细胞通讯。在神经元内部，脉冲会移动到轴突尖端，并导致名为神经递质的化学物质（发挥信使的作用）被释放。

神经递质穿过两个神经细胞之间的间隙（突触），然后附着在接收细胞上的受体部位。

 

通过数学模型来模拟神经元：输入、权重（weight）、加和（summation，∑），激活函数、输出。【1】

 

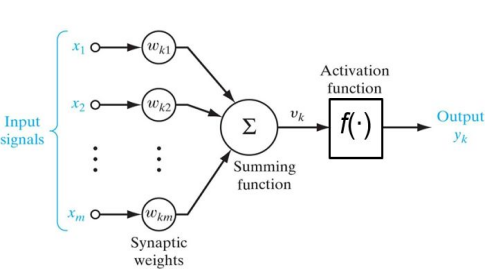
    单个生物神经元的行为似乎很简单，但是它们组成了数十亿个庞大的网络，每个神经元都与数千个其他神经元相连。高度复杂的计算可以通过相当简单的神经元网络来执行，数以亿计的神经元可以组织成复杂大脑皮层。可以通过人工神经网络（Artificial Neural Network，ANN）进行模拟。【4】

 

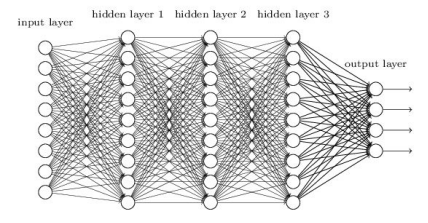
 二、最简单的感知机（Perceptron）：【5】【6】

感知机是由美国学者Frank Rosenblattt 在1957年提出来的,是神经网络最初起源的算法。

感知机接收多个输入信号，输出一个信号。假设感知机的信号只有1/0两种取值。

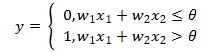
x1,x2是输入；w1,w2是权重(weight),；θ代表阈值（threshold），当w1x1+w2x2>θ代表神经元被激活了（取值1），反之未被激活（取值0）。

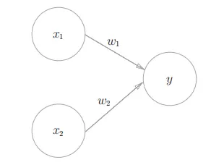
注：一个⚪代表一个神经元

  

1. 与门（AND gate）
   与门是有两个输入和一个输出的门电路。下图是这种输入信号和输出信号的真值表（Truth table）：

如果用感知机来表示与门，可以把（w1,w2,θ）分别设置为（1, 1, 1），或者设置为(0.5, 0.5, 0.8)，实际上有无穷多种取值都可以达成预期。

 

2. 与非门（NAND gate）= 与门（AND gate）+ 非门（NOT gate）
   与非门就是颠倒了与门的输出。用真值表表示的话，如下图所示，仅当x1和x2同时为1时输出0，其他时候则输出1。

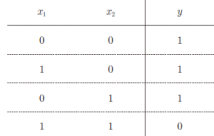
要表示与非门，可以用(w1, w2, θ) = (−0.5, −0.5, −0.7) 这样的组合。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门。

 

3. 或门（OR gate）
   或门是“只要有一个输入信号是1，输出就为1”的逻辑电路

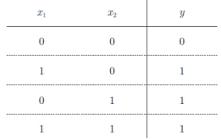
要表示或门，可以用(w1, w2, θ) = (0.5, 0.5, 0.3) 这样的组合。

 

三、从感知机（Perceptron）到深度神经网络（MLP -> DNN）：【5】【6】

1. 感知机的局限性

综上，使用感知机可以实现与门、与非门、或门三种逻辑电路。现在来考虑一下异或门（XOR gate，exclusive OR）

 

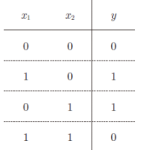
异或门实现的困境：

仅当x1或x2中的一方为1时，才会输出1；

实际上，用前面介绍的感知机是无法实现这个异或门的。我们尝试通过画图来思考其中的原因。

 

首先，我们试着将或门的动作形象化。或门的情况下，当权重参数为(b,w_1,w_2)=(-0.5,1.0,1.0)时，可满足真值表条件。此时，感知机可用如下表达式表示：

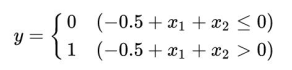
上式表示的感知机会由直线-0.5+x1+x2=0分割的两个空间。其中一个空间输出1，另外一个空间输出0，如图所示。

 

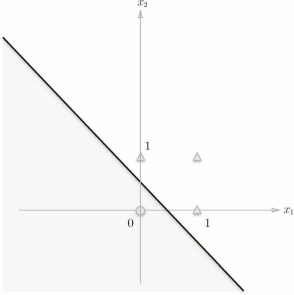
或门在(x1, x2) = (0, 0) 时输出0，在(x1, x2) 为(0, 1)、(1, 0)、(1, 1) 时输出1。上图中，○表示0，△表示1。如果想制作或门，需要用直线将上图中的○和△分开。实际上，刚才的那条直线就将这4 个点正确地分开了。

 

那么，换成异或门的话会如何呢？能否像或门那样，用一条直线作出分割下图中的○和△的空间呢？

 

 

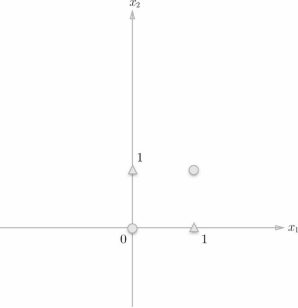
想要用一条直线将上图中的○和△分开，无论如何都做不到。

 

2. 线性和非线性

上图中的○和△无法用一条直线分开，但是如果将“直线”这个限制条件去掉，就可以实现了。比如，我们可以像下图 那样，作出分开○和△的空间。

 

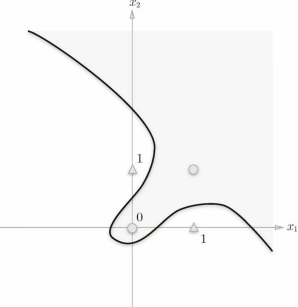
感知机的局限性就在于它只能表示由一条直线分割的空间，像这样弯曲的曲线无法用感知机表示。另外，由图中曲线分割而成的空间称为非线性空间，由直线分割而成的空间称为线性空间。线性、非线性这两个术语在机器学习领域很常见，可以将其想象成图中所示的直线和曲线。

 

3. 多层感知机

感知机虽然不能表示异或门，但感知机的绝妙之处在于它可以“叠加”。

门电路的组合：异或门的制作方法有很多，其中之一就是组合前面的与门、与非门、或门进行配置。

 

异或门可以通过下图所示的配置来实现。这里，x1和x2表示输入信号，y表示输出信号。x1和x2是与非门和或门的输入，而与非门和或门的输出则是与门的输入。

 

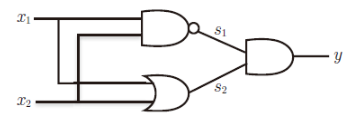
现在来确认一下上图的配置是否真正实现了异或门。这里，把s1作为与非门的输出，把s2作为或门的输出，填入真值表中。结果如下图所示，观察x1、x2、y，可以发现确实符合异或门的输出。

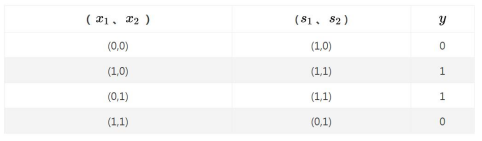
这样，异或门的实现就完成了。下面我们试着用“叠加”感知机的表示方法来表示这个异或门：

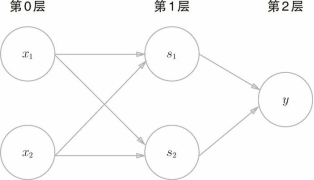
如图，异或门是一种多层结构的神经网络。这里，将最左边的一列称为第 0 层，中间的一列称为第 1 层，最右边的一列称为第 2 层。

实际上，与门、或门是单层感知机，而异或门是2层感知机。叠加了多层的感知机也称为多层感知机MLP（Multi Layer Perceptron）。

更深层次的MLP称为深度神经网络DNN（Deep Neural Networks，一般隐藏层大于2）， 它们都属于全连接神经网络FC（Fully Connected Neural Net）。

 

四、总结【5】【6】

1. 感知机是具有输入和输出的算法。给定一个输入后，将输出一个既定值。
2. 感知机将权重和偏置设定为参数。
3. 使用感知机可以表示与门和或门等逻辑电路。
4. 异或门无法通过单层感知机来表示。
5. 使用2层感知机可以表示异或门。
6. 单层感知机只能表示线性空间，而多层感知机可以表示非线性空间。

 

参考文献（References）：

【1】 唐锐 《从生物神经网络到人工神经网络》

https://www.51cto.com/article/577737.html

 

【2】 AU大脑学院 《神经系统是怎样传递信号控制行为的？》

https://www.sohu.com/a/514481557_121209576

 

【3】 妙佑医疗 《脑工作原理》

https://www.mayoclinic.org/zh-hans/diseases-conditions/epilepsy/in-depth/brain/art-20546821

 

【4】 数据派THU 《从生物学到神经元：人工神经网络 ( ANN ) 简介》

https://blog.csdn.net/tMb8Z9Vdm66wH68VX1/article/details/109233579

 

【5】 _Eason_ 《深度神经网络DNN（一）——感知机》

https://blog.csdn.net/weixin_45768638/article/details/108503658

 

【6】 JokerJason 《深度学习瞎学之路--感知器》

http://www.uml.org.cn/ai/2020051521.asp