codeforces_304C_数学题
Bike is interested in permutations. A permutation of length n is an integer sequence such that each integer from 0 to (n - 1) appears exactly once in it. For example, [0, 2, 1] is a permutation of length 3 while both [0, 2, 2] and [1, 2, 3] is not.
A permutation triple of permutations of length n (a, b, c) is called a Lucky Permutation Triple if and only if  . The sign ai denotes the i-th element of permutation a. The modular equality described above denotes that the remainders after dividing ai + bi by n and dividing ci by n are equal.
. The sign ai denotes the i-th element of permutation a. The modular equality described above denotes that the remainders after dividing ai + bi by n and dividing ci by n are equal.
Now, he has an integer n and wants to find a Lucky Permutation Triple. Could you please help him?
The first line contains a single integer n (1 ≤ n ≤ 105).
If no Lucky Permutation Triple of length n exists print -1.
Otherwise, you need to print three lines. Each line contains n space-seperated integers. The first line must contain permutation a, the second line — permutation b, the third — permutation c.
If there are multiple solutions, print any of them.
5
1 4 3 2 0
1 0 2 4 3
2 4 0 1 3
2
-1
In Sample 1, the permutation triple ([1, 4, 3, 2, 0], [1, 0, 2, 4, 3], [2, 4, 0, 1, 3]) is Lucky Permutation Triple, as following holds:
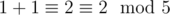 ;
;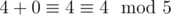 ;
;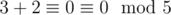 ;
;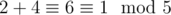 ;
;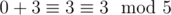 .
.
In Sample 2, you can easily notice that no lucky permutation triple exists.
题目大意:对于一个整数n有元素是0--n-1的排列,求这样的排列3元组,他满足:
分析:
/* 证明有问题
当n是奇数:
n=1时,0,0,0;
0,1,2,……,n/2,……,n-2,n-1
1,2,3,……,n/2+1,……,n-1,0
1,3,5,……,n,……,2(n-1)-1,n-1 (除最后一个数字都是奇数)
第3行对n取模:1,3,5,……,0,……,n-3,n-1(除了n-1, 趋势:一半奇数,一半偶数)
当n是偶数:
因为偶数不会在取模后改变原数字的奇偶性,所以需要我们构造第三行的数字一半是奇数一半是偶数。
已知:
奇数+奇数=偶数
偶数+偶数=偶数
奇数+偶数=奇数
所以需要有n/2对奇数+偶数 (1),n/2对同型相加 (2),然而在n是偶数的情况下奇数有n/2个,偶数也是n/2个,在满足(1)的条件下第一行的奇数用完了偶数,所以(2)不能满足。即偶数不能构造3元组。
*/
#include<iostream> #include<cstdio> #include<cmath> using namespace std; int main() { int n,num1[100005],num2[100005],num3[100005]; scanf("%d",&n); if(n%2==0) printf("-1\n"); else { for(int i=0; i<n; i++) num1[i]=i; for(int i=0; i<n; i++) num2[i]=(i+1)%n; for(int i=0; i<n; i++) num3[i]=(num1[i]+num2[i])%n; for(int i=0; i<n; i++) { printf("%d",num1[i]); if(i==n-1) printf("\n"); else printf(" "); } for(int i=0; i<n; i++) { printf("%d",num2[i]); if(i==n-1) printf("\n"); else printf(" "); } for(int i=0; i<n; i++) { printf("%d",num3[i]); if(i==n-1) printf("\n"); else printf(" "); } } return 0; }





