HDU_1143_tri tiling

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 2834    Accepted Submission(s): 1603

Problem Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

 

 

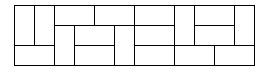
Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30. 

 

 

Output

For each test case, output one integer number giving the number of possible tilings. 

 

 

Sample Input

2 8 12 -1

 

 

Sample Output

3 153 2131

 

 参考：http://blog.csdn.net/chaoojie/article/details/8860935

 

当dp[i] 划分成 2 和 i-2 后，再划分成 4和i-4时，4的部分，不能再划分成2 , 2 组合，这样就会和前面的2 和i-2 重复，同样，划分过2 ，i-2 以及 4, i-4 后，再划分 6, i-6时，也不能划分成 2，2,2 以及 2, 4或 4, 2，同理，划分成8, i-8....

 

把 4， 6， 8.... 看成一整块，就有下图两种情况（正着，倒着）

 

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int main()
{
    int dp[35];
    int t;
    dp[0]=1;
    dp[1]=0;
    dp[2]=3;
    for(int i=3;i<=30;i++)
    {
        if(i%2)
        {
            dp[i]=0;
            continue;
        }
        dp[i]=dp[2]*dp[i-2];
        for(int j=i-4;j>=0;j-=2)
            dp[i]+=2*dp[j];
    }
    while(scanf("%d",&t)&&t!=-1)
    {
        cout<<dp[t]<<endl;
    }
    return 0;
}