cyclic swapping algorithm
原文见:https://leetcode.com/problems/couples-holding-hands/discuss/113362/JavaC%2B%2B-O(N)-solution-using-cyclic-swapping
一、问题引入
假设有一个长度为N的数组nums包含0—N-1的所有数字,但是数组中数字的顺序是随机的。可以任选两个数字进行交换,问最少要用多少步能够使数组满足 i==nums[i](即使数组递增有序)。
二、Cyclic Swapping
使用cyclic swapping的解法:
1.第一步是将N个下标划分为互斥的几个group,每个group是一个环:i0 --> i1 --> ... --> ik --> i0,
其中i0-->i1表示下标为i0的元素应放在i1的位置(即nums[i0]==i1)。
例子:
row: 2, 3, 1, 0, 5, 4
idx: 0, 1, 2, 3, 4, 5
对于上例:
nums[0]=2, 得0-->2;nums[2]=1,得2-->1;nums[1]=3,得1-->3;nums[3]=0,得3-->0;
综上得:0-->2-->1-->3-->0;
同理还可得:4-->5-->4。
这一步的算法:对任意数组nums,对于一个未访问过的下标i0,计算i1使得nums[i0]==i1,接着从i1开始计算i2使得nums[i1]==i2,以此下去,得到 i0 --> i1 --> i2 --> ... --> ik。需要证明该链会从i0开始循环。
此时需证明:
1.最终i0 --> i1 --> i2 --> ... --> ik会循环。
2.且这个环从i0开始循环。
如下图:
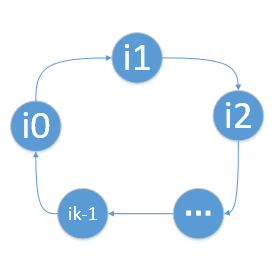
证明1:如果i0 --> i1 --> i2 --> ... --> ik 不会形成环,按照该链生成的规则一直生成下一个i,那么最终会生成一个含有N+1个元素的链,这与题目矛盾。所以该链一定是一个环。
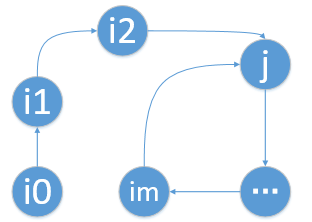
证明2:假设环从一个不为i0的下标j开始循环,那么会形成下图所示,i2-->j且im-->j,则nums[i2]==nums[im],这与题设矛盾。所以该环一定从i0开始循环。
假设现在有两个不同的group,那么两个group一定互斥。因为如果两个group中都存在一个下标j,那么可以根据之前提到的group的生成算法从j开始构造两个group,又因为生成的每一个index仅与它的前驱有关(index==nums[pre]),所以生成的两个group一定是一样的。
2.要使大小为k的group有序(nums[i]==i),最少需要k-1步。group的大小定义为group环中元素个数。
使用数学归纳法证明:
1) 假设group的大小为1,代表已经满足nums[i]==i,需要0步使其有序。所需步数为group的大小减1.
2) 假设group的大小为m时,需m-1步使之有序(1 <= m <= k)
3) 对于大小为k+1的group而言,可以使用一次交换操作将其划分为两个互斥的group1和group2,大小分别为k1和k2,k1+k2==k+1,1 <= k1, k2 <= k:任选下标i和j,将nums[i]和nums[j]交换,交换效果如下图:
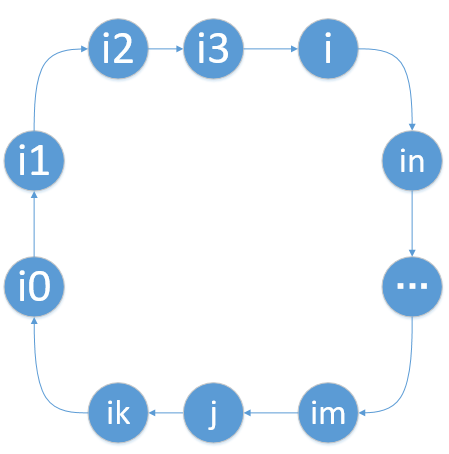
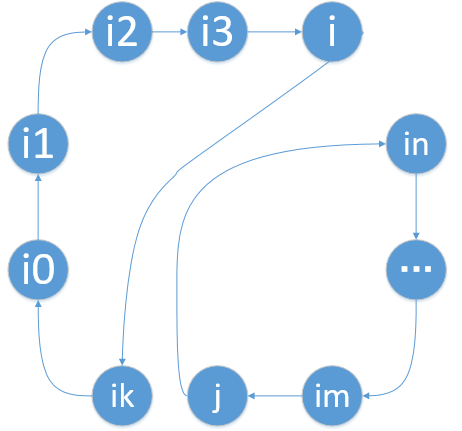
因为2)的缘故,解决group1需要k1-1步,解决group需要k2-1,故解决group的步数为
k1-1+k2-1+1 == k1+k2-1 == k+1-1 == k;
得证:使大小为k的group有序,最少需要k-1步。
综上所述,通过对解决每个group所需的最小交换数求和,可以得到使整个数组有序所需的最小交换数。为了解决每个group,我们可以任意地在group中选择任意两个不同的index并交换indexs上的元素,从而将group缩减为两个较小的不相交的group。在实践中,我们总是可以选择一个pivot,并不断地与它的期望的index交换,直到pivot上的数与期望index相同为止,这意味着整个group被解决,group内的所有nums[i]==i。
相关题目:
leetcode 41 fisrt missing positive: https://www.cnblogs.com/jasonlixuetao/p/10776564.html
leetcode 268 missing number:https://www.cnblogs.com/jasonlixuetao/p/10776701.html


