数据结构与算法(六):散列表
散列表的定义
散列表(hash table),又名‘hash表’,它用的是数组支持按照下标随机访问数据(时间复杂度O(1))的特性,所以散列表其实就是基于数组结构的一种扩展。简单的来说,就是把键值通过散列函数求得hash值之后,对数组容量进行取模运算,得到存放在数组位置的下标值,当我们按照键值查询元素时,我们用同样的方法将键值转化数组下标,从对应的数组下标的位置取数据。散列表这种数据结构虽然支持非常高效的数据插入、删除、查找操作,但是散列表中的数据都是通过散列函数打乱之后无规律存储的。也就说,它无法支持按照某种顺序快速地遍历数据。如果希望按照顺序遍历散列表中的数据,那我们需要将散列表中的数据拷贝到数组中,然后排序,再遍历。因为散列表是动态数据结构,不停地有数据的插入、删除,所以每当我们希望按顺序遍历散列表中的数据的时候,都需要先排序,那效率势必会很低。为了解决这个问题,我们常常会将散列表和链表(或者跳表)结合在一起使用
散列函数
散列函数,顾名思义,它是一个函数。我们可以把它定义成 hash(key),其中 key 表示元素的键值,hash(key) 的值表示经过散列函数计算得到的散列值。设计散列函数的三个基本要求:
- 散列函数计算得到的散列值是一个非负整数;
- 如果 key1 = key2,那 hash(key1) == hash(key2);
- 如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2)。(这一点几乎不可能做到,所以散列冲突也是散列表必须考虑的问题。)
散列函数的好坏,决定了散列冲突的概率大小,也决定了散列表的性能。一个好的散列函数应该具备以下条件:
- 不能太复杂,散列函数设计的太复杂,势必会增加计算时间,进而影响散列表的性能。
- 散列函数生成的值要尽可能随机并均匀分布,这样才能尽量避免或最小化散列冲突,防止出现某个槽内数据特别多的情况。
冲突处理
再好的散列函数也无法避免散列冲突。那究竟该如何解决散列冲突问题呢?我们常用的散列冲突解决方法有两类,开放寻址法(open addressing)和链表法(chaining)。
开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,我们就重新探测一个空闲位置,将其插入。例如当我们往散列表中插入数据时,如果某个数据经过散列函数散列之后,存储位置已经被占用了,我们就从当前位置开始,依次往后查找,看是否有空闲位置,直到找到为止。在查找数据时,我们通过散列函数求出要查找元素的键值对应的散列值,然后比较数组中下标为散列值的元素和要查找的元素。如果相等,则说明就是我们要找的元素;否则就顺序往后依次查找。如果遍历到数组中的空闲位置,还没有找到,就说明要查找的元素并没有在散列表中。因为查找数据时需要根据空闲位置判断数据是否存在,所以在删除数据时,不能直接将位置设置为空,而要采用设置删除标志位的方式。这种方法称为线性探测法,还有另外两种比较经典的探测方法,二次探测(Quadratic probing)和双重散列(Double hashing)。所谓二次探测,跟线性探测很像,线性探测每次探测的步长是 1,那它探测的下标序列就是 hash(key)+0,hash(key)+1,hash(key)+2……而二次探测探测的步长就变成了原来的“二次方”,也就是说,它探测的下标序列就是 hash(key)+0,hash(key)+12,hash(key)+22……所谓双重散列,意思就是不仅要使用一个散列函数。我们使用一组散列函数 hash1(key),hash2(key),hash3(key)……我们先用第一个散列函数,如果计算得到的存储位置已经被占用,再用第二个散列函数,依次类推,直到找到空闲的存储位置。线性探测的简单代码实现如下:
public class HashMap<T>
{
private int _capacity;
private readonly double _loadFactor;
private int _count;
private Node<T>[] _array;
private object _lock = new object();
private IEqualityComparer<string> comparer = EqualityComparer<string>.Default;
public HashMap(int capacity = 8, double loadFactor = 0.75)
{
_capacity = capacity;
_loadFactor = loadFactor;
_array = new Node<T>[capacity];
}
//获取数组下标
private int GetIndex(string key, Node<T>[] array)
{
var hashKey = comparer.GetHashCode(key) & 0x7FFFFFFF;
var index = hashKey % _capacity;
while (array[index] != null)
{
if (array[index].key == key)
break;
index = index == _capacity - 1 ? 0 : index + 1;
}
return index;
}
//动态扩容
private void Dilatation()
{
var currLoadFactor = ((double)_count) / _capacity;
if (currLoadFactor > _loadFactor)
{
_capacity *= 2;
var array = new Node<T>[_capacity];
foreach (var item in _array)
{
if (item != null)
{
Set(item.key, item.value, array);
}
}
_array = array;
}
}
private void Set(string key, T value, Node<T>[] array)
{
var index = GetIndex(key, array);
array[index] = new Node<T>()
{
key = key,
value = value
};
}
public void Set(string key, T value)
{
lock (_lock)
{
Dilatation();
Set(key, value, _array);
_count++;
}
}
public bool Get(string key, out T value)
{
lock (_lock)
{
int index = GetIndex(key, _array);
var node = _array[index];
if (node == null)
{
value = default(T);
return false;
}
else
{
value = node.value;
return true;
}
}
}
class Node<T>
{
public string key { get; set; }
public T value { get; set; }
}
}
链表法
链表法是一种更加常用的散列冲突解决办法,相比开放寻址法,它要简单很多。我们来看这个图,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。当插入的时候,我们只需要通过散列函数计算出对应的散列槽位,将其插入到对应链表中即可,所以插入的时间复杂度是 O(1)。当查找、删除一个元素时,我们同样通过散列函数计算出对应的槽,然后遍历链表查找或者删除。
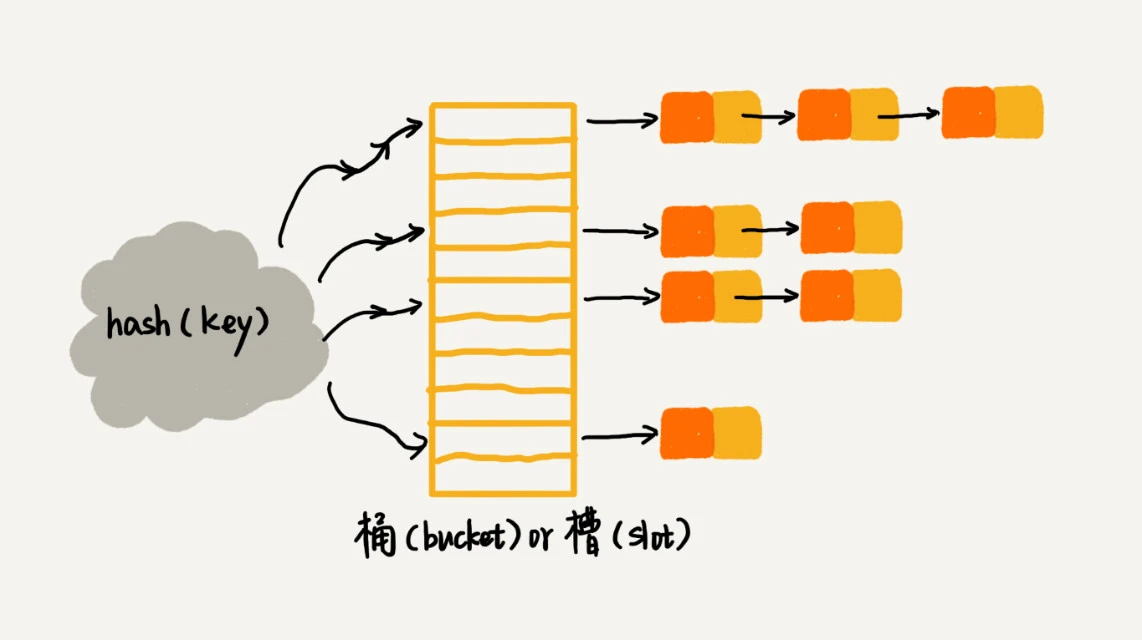
简易代码实现如下:
public class LinkedHashMap<T> : IHashMap<T>
{
private int _capacity;
private readonly double _loadFactor;
private IEqualityComparer<string> comparer = EqualityComparer<string>.Default;
private LinkList<Node<T>>[] _array;
private int _count = 0;
public LinkedHashMap(int capacity = 8, double loadFactor = 0.75)
{
_capacity = capacity;
_loadFactor = loadFactor;
_array = new LinkList<Node<T>>[_capacity];
}
private int GetIndex(string key)
{
var hashKey = comparer.GetHashCode(key) & 0x7FFFFFFF;
var index = hashKey % _capacity;
return index;
}
//动态扩容
private void Dilatation()
{
var currLoadFactor = ((double)_count) / _capacity;
if (currLoadFactor > _loadFactor)
{
_capacity *= 2;
var array = new LinkList<Node<T>>[_capacity];
_count = 0;
foreach (var item in _array)
{
if (item != null)
{
var node = item.First();
while (node != null)
{
Set(node.data.key, node.data.value, array);
node = node.next;
}
}
}
_array = array;
}
}
private void Set(string key, T value, LinkList<Node<T>>[] array)
{
var index = GetIndex(key);
if (array[index] == null)
{
var linkList = new LinkList<Node<T>>();
linkList.Insert(new Node<T>()
{
key = key,
value = value
});
array[index] = linkList;
}
else
{
array[index].Insert(new Node<T>()
{
key = key,
value = value
});
}
_count++;
}
public bool Get(string key, out T value)
{
var index = GetIndex(key);
if (_array[index] == null)
{
value = default(T);
return false;
}
else
{
var node = _array[index].First();
while (node != null)
{
if (node.data.key == key)
{
value = node.data.value;
return true;
}
else
{
node = node.next;
}
}
value = default(T);
return false;
}
}
public void Set(string key, T value)
{
Dilatation();
Set(key, value, _array);
}
class Node<T>
{
public string key { get; set; }
public T value { get; set; }
}
}
装载因子
装载因子的计算公式: 散列表的装载因子=填入表中的元素个数/散列表的长度 ,可以看出装载因子越大,说明表中的元素个数越多,冲突越多,散列表的性能会下降。当超过一定的阈值时,散列表的时间复杂度可能会降低到O(n),这是让人无法让人接受的,但我们可以通过动态扩容的方式解决这个问题。当装载因子过大时,重新申请一个更大的散列表,将数据搬移到这个新散列表中。假设每次扩容我们都申请一个原来散列表大小两倍的空间。如果原来散列表的装载因子是 0.8,那经过扩容之后,新散列表的装载因子就下降为原来的一半,变成了 0.4。针对散列表的扩容,数据搬移操作相对复杂一些。因为散列表的大小变了,数据的存储位置也变了,所以我们需要通过散列函数重新计算每个数据的存储位置。上述方案存在一个问题,当散列表进行扩容时,由于需要进行数据迁移,所以本次插入会变得很慢,针对这个问题,我们可以选择惰性迁移的方式,当装载因子超过阈值时,重新申请一个更大的散列表,但是不进行全部的数据迁移,而是将一小部分数据进行迁移,后面每次插入新数据时,再逐次一小部分的进行迁移,直至将旧的散列表搬空。对于查询操作,为了兼容了新、老散列表中的数据,我们先从新散列表中查找,如果没有找到,再去老的散列表中查找即可。
散列表的应用
Word 文档中单词拼写检查功能是如何实现的?
常用的英文单词有 20 万个左右,假设单词的平均长度是 10 个字母,平均一个单词占用 10 个字节的内存空间,那 20 万英文单词大约占 2MB 的存储空间,就算放大 10 倍也就是 20MB。对于现在的计算机来说,这个大小完全可以放在内存里面。所以我们可以用散列表来存储整个英文单词词典。当用户输入某个英文单词时,我们拿用户输入的单词去散列表中查找。如果查到,则说明拼写正确;如果没有查到,则说明拼写可能有误,给予提示。借助散列表这种数据结构,我们就可以轻松实现快速判断是否存在拼写错误。
LRU 缓存淘汰算法
借助散列表,我们可以把 LRU 缓存淘汰算法的时间复杂度降低为 O(1)。首先,我们需要维护一个按照访问时间从大到小有序排列的链表结构。因为缓存大小有限,当缓存空间不够,需要淘汰一个数据的时候,我们就直接将链表头部的结点删除。当要缓存某个数据的时候,先在链表中查找这个数据。如果没有找到,则直接将数据放到链表的尾部;如果找到了,我们就把它移动到链表的尾部。因为查找数据需要遍历链表,所以单纯用链表实现的 LRU 缓存淘汰算法的时间复杂很高,是 O(n)。一个缓存(cache)系统主要包含下面这几个操作:往缓存中添加一个数据、从缓存中删除一个数据、在缓存中查找一个数据。如果我们将散列表和链表两种数据结构组合使用,可以将这三个操作的时间复杂度都降低到 O(1)。
- 查找数据:通过散列表,我们可以很快地在缓存中找到一个数据。当找到数据之后,我们还需要将它移动到双向链表的尾部。
- 删除数据:我们需要找到数据所在的结点,然后将结点删除。借助散列表,我们可以在 O(1) 时间复杂度里找到要删除的结点。因为我们的链表是双向链表,双向链表可以通过前驱指针 O(1) 时间复杂度获取前驱结点,所以在双向链表中,删除结点只需要 O(1) 的时间复杂度
- 添加数据:添加数据到缓存稍微有点麻烦,我们需要先看这个数据是否已经在缓存中。如果已经在其中,需要将其移动到双向链表的尾部;如果不在其中,还要看缓存有没有满。如果满了,则将双向链表头部的结点删除,然后再将数据放到链表的尾部;如果没有满,就直接将数据放到链表的尾部。
具体结构如下:
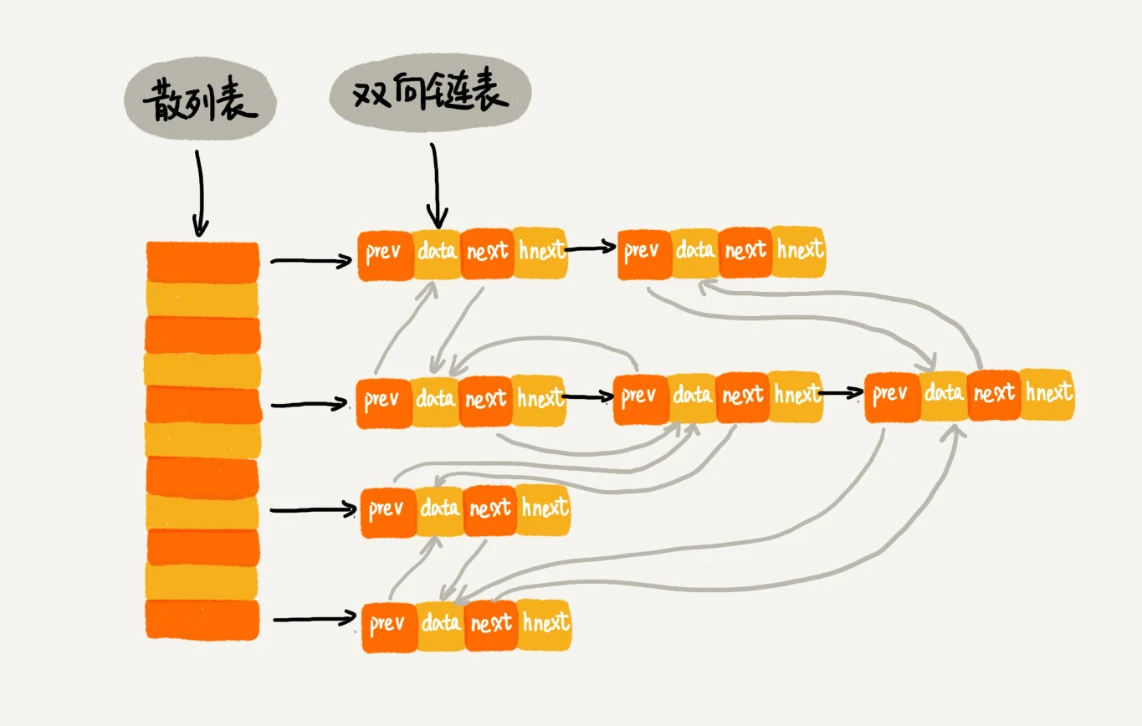
简易代码实现如下:
public class LruLinkList<T>
{
private Node<T> _head;
private Node<T> _tail;
private int _capacity;
private HashTable _hashTable;
private int _count = 0;
public LruLinkList(int capacity = 8)
{
_capacity = capacity;
_hashTable = new HashTable(capacity);
}
public void Set(string key, T value)
{
if (_hashTable.Get(key, out var existNode))
{
existNode.value = value;
LruMove(existNode);
}
else
{
if (_count == _capacity)
{
_hashTable.Delete(_head.key);
_head = _head.next;
_head.prev = null;
_count--;
}
if (_head == null)
{
_head = new Node<T>();
_head.key = key;
_head.value = value;
_tail = _head;
_hashTable.Set(key, _head);
}
else
{
var node = new Node<T>();
node.key = key;
node.value = value;
_tail.next = node;
node.prev = _tail;
_tail = node;
_hashTable.Set(key, node);
}
_count++;
}
}
public bool Get(string key, out T value)
{
if (_hashTable.Get(key, out var node))
{
LruMove(node);
value = node.value;
return true;
}
else
{
value = default(T);
return false;
}
}
private void LruMove(Node<T> node)
{
if (node.key != _tail.key)
{
if (node.key == _head.key)
{
node.next.prev = null;
_head = node.next;
MoveToTail(node);
}
else
{
node.prev.next = node.next;
node.next.prev = node.prev;
MoveToTail(node);
}
}
}
private void MoveToTail(Node<T> node)
{
node.prev = _tail;
node.next = null;
_tail.next = node;
_tail = node;
}
public List<T> FindAll()
{
var list = new List<T>();
var node = _head;
while (node != null)
{
list.Add(node.value);
node = node.next;
}
return list;
}
public class Node<T>
{
public string key { get; set; }
public T value { get; set; }
public Node<T> next { get; set; }
public Node<T> prev { get; set; }
public Node<T> hnext { get; set; }
}
public class HashTable
{
private HashNode[] array;
private IEqualityComparer<string> comparer = EqualityComparer<string>.Default;
private int _capacity;
public HashTable(int capacity)
{
array = new HashNode[capacity];
_capacity = capacity;
}
public bool Get(string key, out Node<T> value)
{
var index = GetIndex(key);
if (array[index] != null)
{
var tempNode = array[index].node;
while (tempNode != null)
{
if (tempNode.key == key)
{
value = tempNode;
return true;
}
tempNode = tempNode.hnext;
}
}
value = default(Node<T>);
return false;
}
public void Set(string key, Node<T> node)
{
var index = GetIndex(key);
if (array[index] != null)
{
var tempNode = array[index].node;
while (tempNode.hnext != null)
{
tempNode = tempNode.hnext;
}
tempNode.hnext = node;
}
else
{
array[index] = new HashNode()
{
key = key,
node = node
};
}
}
public void Delete(string key)
{
var index = GetIndex(key);
if (array[index] != null)
{
var tempNode = array[index].node;
var isFirst = true;
Node<T> lastNode = null;
while (tempNode != null)
{
if (tempNode.key == key)
{
if (isFirst)
{
if (tempNode.hnext != null)
{
array[index].key = tempNode.hnext.key;
array[index].node = tempNode.hnext;
}
else
{
array[index] = null;
}
}
else
{
lastNode.hnext = tempNode.hnext;
}
return;
}
isFirst= false;
lastNode = tempNode;
tempNode = tempNode.hnext;
}
}
}
private int GetIndex(string key)
{
var hashKey = comparer.GetHashCode(key) & 0x7FFFFFFF;
return hashKey % _capacity;
}
public class HashNode
{
public string key { get; set; }
public Node<T> node { get; set; }
}
}
}


