bzoj1977 次小生成树

Description

小 C 最近学了很多最小生成树的算法，Prim 算法、Kurskal 算法、消圈算法等等。 正当小 C 洋洋得意之时，小 P 又来泼小 C 冷水了。小 P 说，让小 C 求出一个无向图的次小生成树，而且这个次小生成树还得是严格次小的，也就是说： 如果最小生成树选择的边集是 EM，严格次小生成树选择的边集是 ES，那么需要满足：(value(e) 表示边 e的权值)  这下小 C 蒙了，他找到了你，希望你帮他解决这个问题。

Input

第一行包含两个整数N 和M，表示无向图的点数与边数。 接下来 M行，每行 3个数x y z 表示，点 x 和点y之间有一条边，边的权值为z。

Output

包含一行，仅一个数，表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)

Sample Input

5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6

Sample Output

11

HINT

 

数据中无向图无自环； 50% 的数据N≤2 000 M≤3 000； 80% 的数据N≤50 000 M≤100 000； 100% 的数据N≤100 000 M≤300 000 ，边权值非负且不超过 10^9 。

 

首先应该想到的暴力是：枚举每一条树边，然后再枚举非树边。但是这样的时间复杂度是m^2只能过50%

后来可以考虑，先进行一遍最小生成树，然后对于每一条非树边，找到这个非树边起点、终点在树上位置，然后求出这两个点最短路径上的最大边，再以这条非树边进行替换。

如图，红边是非树边，我们需要找到u，v两点的树上路径的最长边，然后替换为红边：

 

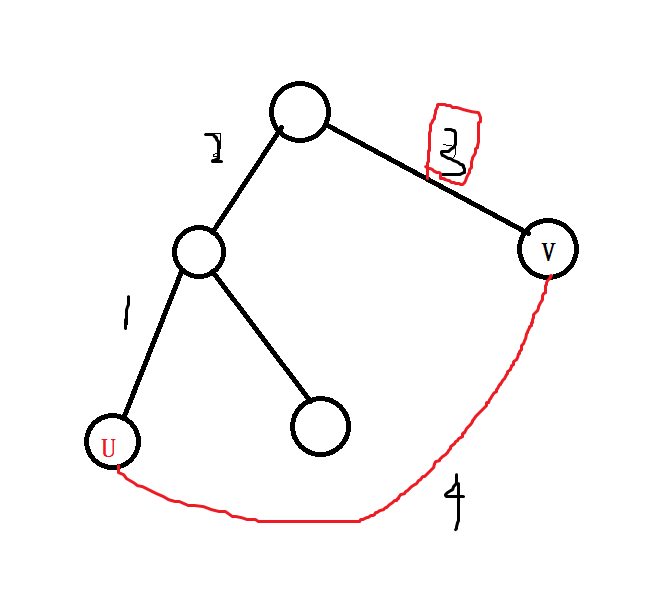
但是！如果这条最长边是等于那条非树边的，就不能替换。故此我们需要记录次长边并且保证次长边严格小于最长边。

那么问题来了：怎么记录最长、次长边？怎么找到两个点之间的最短距离？

显而易见，我们需要用倍增LCA来解决.没有学过LCA的同学可以先去写一下模板再做这道题。

我们记录tree[i][j]代表i点向上2^j的点得编号

maxx[i][j]表示i向上2^j的最大值，maxn[i][j]表示次大值。

根据LCA基本算法，我们能得出：tree[i][j]=tree[tree[i][j-1][j-1]，其中maxn、maxx的具体维护看代码，主要是不重不漏（我开始漏了一种情况，调了一下午）

预处理出tree等数组，跑LCA时，记录ma为这条最短路上的最长路径，边跑变更新，但一定记住要时刻保证ma不等于更新的那条非树边！

最后ans=sum(最小生成树和)-ma+val[i]（非树边边权）

代码如下：

#include <iostream>
#include <cstdio> 
#include <algorithm>
#include <cstring>
#include <queue>
#define REP(i,k,n)  for(int i=k;i<=n;i++)
#define in(a) a=read()
#define MAXN 100010
using namespace std;
inline int read(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar())
        if(ch=='-')
            f=-1;
    for(;isdigit(ch);ch=getchar())
        x=x*10+ch-'0';
    return x*f;
}
queue <int> Q;
long long sum=0,ans=(1ll<<50); 
int n,m;
int cnt,book[MAXN<<2],f[MAXN];
int vis[MAXN],depth[MAXN],tree[MAXN][30],maxx[MAXN][30],maxn[MAXN][30];
int total=0,head[MAXN],to[MAXN<<2],nxt[MAXN<<2],val[MAXN<<2];
struct node{
    int x,y,z;
}l[MAXN<<2];
bool cmp(node a,node b){
    return a.z<b.z;
}
inline int getf(int k){
    if(f[k]==k)  return k;
    return f[k]=getf(f[k]);
}
inline void adl(int a,int b,int c){
    total++;
    to[total]=b;
    val[total]=c;
    nxt[total]=head[a];
    head[a]=total;
    return ;
}
inline void BFS(){//预处理
    Q.push(1);
    depth[1]=1;
    vis[1]=1;
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        REP(j,1,21){
            tree[u][j]=tree[tree[u][j-1]][j-1];
            if(maxx[u][j-1]>maxx[tree[u][j-1]][j-1]){
                maxx[u][j]=maxx[u][j-1];
                maxn[u][j]=max(maxx[tree[u][j-1]][j-1],maxn[u][j-1]);
            }
            if(maxx[u][j-1]<maxx[tree[u][j-1]][j-1]){
                maxx[u][j]=maxx[tree[u][j-1]][j-1];
                maxn[u][j]=max(maxx[u][j-1],maxn[tree[u][j-1]][j-1]);
            }
            if(maxx[u][j-1]==maxx[tree[u][j-1]][j-1]){
                maxx[u][j]=maxx[u][j-1];
                maxn[u][j]=max(maxn[u][j-1],maxn[tree[u][j-1]][j-1]);
            }
        }
        for(int e=head[u];e;e=nxt[e])
            if(!vis[to[e]]){
                vis[to[e]]=1;
                depth[to[e]]=depth[u]+1;
                tree[to[e]][0]=u;
                maxx[to[e]][0]=val[e];
                Q.push(to[e]);
            }
    }
    return ;
}
inline int lca(int u,int v,int c){//lca
    if(depth[u]<depth[v])  swap(u,v);
    int d=depth[u]-depth[v];
    int ma=-999999999;
    for(int i=0;(1<<i)<=d;i++)//提到同一高度
        if((1<<i)&d){
            if(maxx[u][i]==c)  ma=max(ma,maxn[u][i]);
            else  ma=max(ma,maxx[u][i]);
            u=tree[u][i];
        //    cout<<u<<" "<<ma<<endl;
        }
    if(u==v){
        if(ma==-999999999)  return 0;
        return ma;
    }
    for(int i=21;i>=0;i--)//两点开跑
        if(tree[u][i]!=tree[v][i]){
            if(maxx[u][i]==c && maxx[v][i]==c)  
                ma=max(ma,max(maxn[u][i],maxn[v][i]));
            if(maxx[u][i]==c && maxx[v][i]!=c)
                ma=max(ma,max(maxn[u][i],maxx[v][i]));
            if(maxx[v][i]==c && maxx[u][i]!=c)
                ma=max(ma,max(maxn[v][i],maxx[u][i]));
            if(maxx[u][i]!=c && maxx[v][i]!=c)
                ma=max(ma,max(maxx[v][i],maxx[u][i]));
            u=tree[u][i];
            v=tree[v][i];
        }//最后lca是他们的父亲，所以要再更新一次
    if(maxx[u][0]==c && maxx[v][0]==c)  
        ma=max(ma,max(maxn[u][0],maxn[v][0]));
    if(maxx[u][0]==c && maxx[v][0]!=c)
        ma=max(ma,max(maxn[u][0],maxx[v][0]));
    if(maxx[v][0]==c && maxx[u][0]!=c)
        ma=max(ma,max(maxn[v][0],maxx[u][0]));
    if(maxx[u][0]!=c && maxx[v][0]!=c)
        ma=max(ma,max(maxx[v][0],maxx[u][0]));
    return ma;
}
int main(){
    in(n);in(m);
    REP(i,1,n)  f[i]=i;
    REP(i,1,m){
        in(l[i].x);
        in(l[i].y);
        in(l[i].z);
    }
    sort(l+1,l+m+1,cmp);
    REP(i,1,m){
        int f1=getf(l[i].x),f2=getf(l[i].y);
        if(f1!=f2){
            cnt++;
            book[i]=1;
            f[f2]=f1;
            sum+=(long long)l[i].z;
            adl(l[i].x,l[i].y,l[i].z);
            adl(l[i].y,l[i].x,l[i].z);
        }
        if(cnt==n-1)  break;
    }
    BFS();
    REP(i,1,m)
        if(!book[i]){//枚举所有的非树边
        //    cout<<l[i].x<<" "<<l[i].y<<" "<<l[i].z<<endl;
        //    cout<<lca(l[i].x,l[i].y,l[i].z)<<endl;
            ans=min(ans,sum-(long long)lca(l[i].x,l[i].y,l[i].z)+(long long)l[i].z);
        }
    cout<<ans;
}