Dijkstra 最短路径算法 秒懂详解
想必大家一定会Floyd了吧,Floyd只要暴力的三个for就可以出来,代码好背,也好理解,但缺点就是时间复杂度高是O(n³)。
于是今天就给大家带来一种时间复杂度是O(n²),的算法:Dijkstra(迪杰斯特拉)。
这个算法所求的是单源最短路,好比说你写好了Dijkstra的函数,那么只要输入点a的编号,就可算出图上每个点到这个点的距离。
我先上一组数据(这是无向图):
5 6 1 2 5 1 3 8 2 3 1 2 4 3 4 5 7 2 5 2
图大概是这个样子:
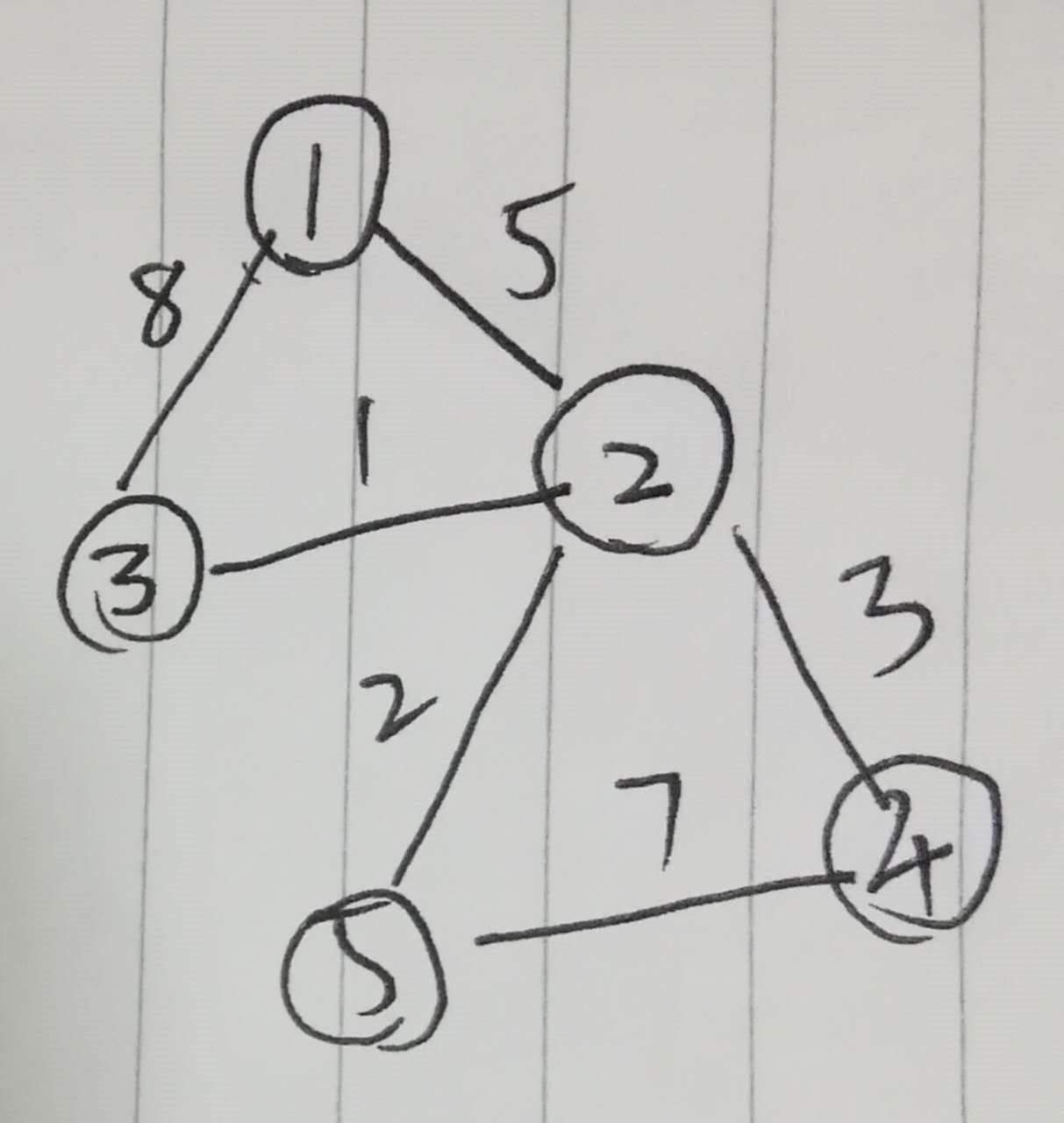
Dijkstra 算法是一种类似于贪心的算法,步骤如下:
1、当到一个时间点时,图上部分的点的最短距离已确定,部分点的最短距离未确定。
2、选一个所有未确定点中离源点最近的点,把他认为成最短距离。
3、再把这个点所有出边遍历一边,更新所有的点。
下面模拟一下:
我们以1为源点,来求所有点到一号点的最短路径。
先建立一个dis数组,dis[i]表示第i号点到源点(1号点)的估计值,你可能会问为什么是估计值,因为这个估计值会不断更新,更新到一定次数就变成答案了,这个我们一会再说。
然后我们在建立一个临界矩阵,叫做:map,map[i][j]=v表示从i到j这条边的权值是v。
dis初始值除了源点本身都是无穷大。源点本身都是0.
先从1号点开始。一号点,map[1][2]=5,一号点离2号点是5,比无穷大要小,所以dis[2]从无穷大变成了5。顺便,我们用minn记录距离1号点最短的点,留着以后会用。
dis[0,5,∞,∞,∞]。minn=2。
然后搜到3号点,map[1][3]=8,距离是8,比原来的dis[3]的∞小,于是dis[3]=8。但是8比dis[2]的5要大,所以minn不更新。
dis[0,5,8,∞,∞]
接着分别搜索4,5号点,发现map[1][4],map[1][5]都是∞,所以就不更新。
现在,dis数组所呈现的明显不是最终答案,因为我们才更新一遍,现在我们开始第二次更新,第二次更新以什么为开始呢?就是以上一次我们存下来的,minn,相当于把2当源点,求所有点到它的最短路,加上它到真正的源点(1号点)的距离,就是我们要求的最短路。
从2号点开始,搜索3号点,map[2][3]=1,原本dis[3]=8,发现dis[2]+map[2][3]=5+1=6<dis[3](8)所以更新dis[3]为6,minn=3
dis[0,5,6,∞,∞] minn=3.
然后搜索4号点,map[2][4]=3,原本dis[4]=∞,所以,dis[2]+map[2][4]=5+3=8<dis[4](∞)所以更新dis[4]=8,因为map[2][4]=3,3>1,minn不更新。
dis[0,5,6,8,∞] minn=3.
接着搜索5号点,map[2][5]=2,5+2=7,7<∞,dis[5]=7minn不变。
dis[0,5,6,8,7]
二号点搜完,因为minn是3,继续搜索3号点。
三号点还是按照二号点的方法搜索,发现没有可以更新的,然后搜索四号。
四号搜5号点,发现8+7>5+2,所以依然不更新,然后跳出循环。
现在的估计值就全部为确定值了:
dis[0,5,6,8,7]
这就是每个点到源点一号点的距离,我们来看一下代码:
#include <iostream> #include <algorithm> #include <cmath> #include <cstdio> #include <cstring> #include <cstdlib> using namespace std; int map[110][110];//这就是map数组,存储图 int dis[10010];//dis数组,存储估计值 int book[10010];//book[i]代表这个点有没有被当做源点去搜索过,1为有,0为没有。这样就不会重复搜索了。 int n,m; void dijkstra(int u)//主函数,参数是源点编号 { memset(dis,88,sizeof(dis));//把dis数组附最大值(88不是十进制的88,其实很大) int start=u;//先从源点搜索 book[start]=1;//标记源点已经搜索过 for(int i=1;i<=n;i++) { dis[i]=min(dis[i],map[start][i]);//先更新一遍 } for(int i=1;i<=n-1;i++) { int minn=9999999;//谢评论区,改正一下:这里的minn不是题解上的minn,这代表的是最近点到源点的距离,start才代表最近的点、 for(int j=1;j<=n;j++) if(book[j]==0 && minn>dis[j]) { minn=dis[j]; start=j;//找到离源点最近的点,然后把编号记录下来,用于搜索。 } book[start]=1; for(int j=1;j<=n;j++) dis[j]=min(dis[j],dis[start]+map[start][j]);//以新的点来更新dis。 } } int main() { cin>>n>>m; memset(map,88,sizeof(map)); for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; map[a][b]=c; } for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(i==j) map[i][j]=0; dijkstra(1);//以1为源点。 for(int i=1;i<=n;i++) cout<<dis[i]<<" "; }
这就是用邻接矩阵实现dijkstra,但是这个算法有一个坏处,就是出现负权边,这个算法就炸了,要解决负权边,我以后会给大家带来Bell man ford(SPFA)
这个算法的复杂度是O(n²),空间复杂度也是n平方,如果用邻接表来实现,最差情况,时间复杂度是O(n*m)似乎比n²要大一些,但是空间复杂度会从n平方变成m,少了很多,现在我呈上邻接表的代码。
#include <iostream> #include <algorithm> #include <cmath> #include <cstdio> #include <cstring> #include <cstdlib> using namespace std; int value[10010],to[10010],next[10010]; int head[10010],total; int book[10010]; int dis[10010]; int n,m; void adl(int a,int b,int c) { total++; to[total]=b; value[total]=c; next[total]=head[a]; head[a]=total; } void dijkstra(int u) { memset(dis,88,sizeof(dis)); memset(book,0,sizeof(book)); dis[u]=0; for(int i=1;i<=n;i++) { int start=-1; for(int j=1;j<=n;j++) if(book[j]==0 && (dis[start]>dis[j] || start==-1)) start=j; book[start]=1; for(int e=head[start];e;e=next[e]) dis[to[e]]=min(dis[to[e]],dis[start]+value[e]); } } int main() { cin>>n>>m; for(int i=1;i<=m;i++) { int a,b,c; cin>>a>>b>>c; adl(a,b,c); } dijkstra(1); for(int i=1;i<=n;i++) cout<<dis[i]<<" "; }
一年多了,身为一个OIer,经历了太多。
当年那么畏惧的Dijkstra、邻接表,现在已经是信手拈来。
那个暑假,因为Djkstra名字的朗朗上口,讲自己名字改为了Dijkstra,但是逐渐因为SPFA的可处理负权边,也将Dijkstra,淡忘。
如今突然想起,加入了堆优化,有人说:一道题如果边权没有负数,那么一定是在卡SPFA。这时候就用到了堆优化的Dijkstra。
一年前提到,朴素的Dijkstra时间复杂度是n^2,被SPFA的m*常数吊打,但是,经过堆优化,Dijkstra的时间复杂度能达到nlogn,如果这个图特别稠密的话,也就是m特别大(比如完全图就是n^2),那么nlogn是要小于m的,这就用到了Dijkstra
首先堆优化怎么优化?观察上面的代码,每次循环中都再嵌套一个循环求dis值最小的点。这里,我们可以用一个优先队列,每当搜索到一个新点,扔到优先队列里面,这样每次就取队首的绝对是最优值。这样可以省去for循环。
#include <iostream> #include <cstdio> #include <cstdlib> #include <cmath> #include <cstring> #include <algorithm> #include <queue> #define in(a) a=read() #define REP(i,k,n) for(long long i=k;i<=n;i++) #define MAXN 10010 using namespace std; typedef pair<long long,long long> P; inline long long read(){ long long x=0,t=1,c; while(!isdigit(c=getchar())) if(c=='-') t=-1; while(isdigit(c)) x=x*10+c-'0',c=getchar(); return x*t; } long long n,m,s; long long total=0,head[MAXN],nxt[MAXN<<10],to[MAXN<<10],val[MAXN<<10]; long long dis[MAXN],vis[MAXN]; priority_queue <P, vector<P>,greater<P> > Q;//优先队列优化 inline void adl(long long a,long long b,long long c){ total++; to[total]=b; val[total]=c; nxt[total]=head[a]; head[a]=total; return ; } inline void Dijkstra(){ REP(i,1,n) dis[i]=2147483647; dis[s]=0; Q.push(P(0,s)); while(!Q.empty()){ long long u=Q.top().second;//取出dis最小的点 Q.pop();//弹出 if(vis[u]) continue; vis[u]=1; for(long long e=head[u];e;e=nxt[e]) if(dis[to[e]]>dis[u]+val[e]){ dis[to[e]]=dis[u]+val[e]; Q.push(P(dis[to[e]],to[e]));//插入 } } return ; } int main(){ in(n),in(m),in(s); long long a,b,c; REP(i,1,m) in(a),in(b),in(c),adl(a,b,c); Dijkstra(); REP(i,1,n) printf("%lld ",dis[i]); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号