图论-最小生成树
首先来了解一下定义：
- 生成树的定义：在一个任意连通图G中，如果取它的全部顶点和一部分边构成一个子图G‘ , 即：V（G’）=V（G）和
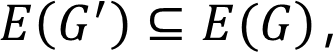若同时满足：
1.边集E(G‘)中的所有边能够使全部顶点连通 2.不形成任何回路 则称子图G’是原图G的一颗生成树。
- 最小生成树的定义： 所有生成树中权值和最小的生成树即为最小生成树。
根据定义，要产生最小生成树，首先要保证图是连通的。怎样判断呢？有三种方法：BFS,DFS,和并查集。 这里甩出一个非常清晰的文章供参考：https://www.cnblogs.com/Roni-i/p/8456657.html
/***************************************************************************************************************************************************************************************/
好啦，判断出连通图后，我们就要求最小生成树了！我学习了两种算法：Prim 和 Kruskal.
prim算法
prim是一种贪心算法：
证明：https://blog.csdn.net/abcef31415926/article/details/52684829 可用反证法证明。
下面给出洛谷P3366计算最小生成树的AC代码——（用了vector数组建图，BFS判断连通图，和prim算法）
#include <bits/stdc++.h> //洛谷裸题，先用dfs判断连通图，然后用prim using namespace std; #define INF 0x3f3f3f3f const int maxn=2e5+10; vector<int> G[maxn],W[maxn]; int n,m; int vis[5010]; int dis[5010]; //dfs判断是不是连通图 void dfs(int x){ vis[x]=1; int num=G[x].size(); for(int i=0;i<num;i++){ if(!vis[G[x][i]]) dfs(G[x][i]); } } long long ans=0; int prim(){ // for(int i=0;i<5010;i++) vis[i]=0; // for(int i=0;i<5010;i++) dis[i]=INF; 可以用memset来初始化 memset(vis,0,sizeof(vis)); memset(dis,INF,sizeof(dis)); int num=G[1].size(); for(int i=0;i<num;i++){ //初始化：和1相邻的点到 1的距离是点集B到A的距离最小值 dis[G[1][i]]=min(dis[G[1][i]],W[1][i]); } vis[1]=1; for(int i=1;i<n;i++){ //执行n-1次，添加n-1条边 int u=0; for(int j=1;j<=n;j++){ if(!vis[j] && dis[u]>dis[j]){ u=j; } } vis[u]=1; ans+=dis[u]; num=G[u].size(); for(int j=0;j<num;j++){ //更新加入点后的dis dis[G[u][j]]=min(dis[G[u][j]],W[u][j]); } } return ans; } int main(int argc, char** argv) { int x,y,z; cin>>n>>m; for(int i=0;i<m;i++){ cin>>x>>y>>z; G[x].push_back(y); //一定要注意！！无向图两种方向push进去！ W[x].push_back(z); G[y].push_back(x); W[y].push_back(z); } dfs(1); for(int i=1;i<=n;i++){ if(!vis[i]){ cout<<"orz"<<endl; return 0; } } ans=prim(); cout<<ans<<endl; return 0; }
prim算法的复杂度是 （n2+m）.可以用优先队列来优化，因为我们发现，每次为了找出距离点集A最小的边，都要遍历所有的点，并且A加入新的点后，还要更新所有与该点相连的点到A的距离。如果用优先队列维护，每次push进去后，只需要logm的时间维护这个队列（最坏情况是所有的边都push进去），pop只需要O（1）的时间。添加n-1个点，所以复杂度降为了（nlogm）
int head[MAXN],to[MAXN],nxt[MAXN],w[MAXN],o; bool vis[MAXN]; int dis[MAXN]; void add_edge(int a,int b,int c){ nxt[o]=head[a]; to[o]=b; w[o]=c; head[a]=o++; nxt[o]=head[b]; to[o]=a; w[o]=c; head[b]=o++; } typedef pair<int,int> PII; int prim(int n) { memset(vis,0,sizeof(vis)); priority_queue<PII,vector<PII>,greater<PII> > Q; int ret=0; vis[1]=1; for(int i=head[1];~i;i=nxt[i]) Q.push({w[i],to[i]}); while(!Q.empty()){ int val=Q.top().first; int x=Q.top().second; Q.pop(); if(vis[x]) continue; vis[x]=1; ret+=val; for(int i=head[x];~i;i=nxt[i]) if(!vis[to[i]]) Q.push({w[i],to[i]}); } return ret; }
Kruskal算法
Kruskal算法依然是贪心将图G中的边按权值从小到大的顺序依次选取每一条边，对于每一条边：
若选取的一条边使生成树不产生回路，把它并入生成树的边集中；
若选取的一条边使生成树产生回路，舍弃。
重复进行直至最小生成树包含n-1条边。时间复杂度：（mlogm）
证明：https://www.cnblogs.com/tahitian-fang/p/5751298.html
下面依然是洛谷P3366的AC代码：
#include <bits/stdc++.h> using namespace std; const int maxn=2e5+10; struct edge{ //kruskal算法和这种存图方式一般是配套的 int u,v,w; bool operator <(const edge &t)const{ return w<t.w; } }edges[maxn]; int n,m; long long ans=0; int fa[5010]; int find(int x){ return x==fa[x]?x:fa[x]=find(fa[x]); } void merge(int x,int y){ //注意！！这里应该是find(x),而不是比较fa[x]和fa[y]! x=find(x); y=find(y); if(x==y) return ; else fa[x]=y; } bool liantong(){ //用并查集判断是否连通 for(int i=1;i<=n;i++) fa[i]=i; for(int i=0;i<m;i++){ merge(edges[i].u,edges[i].v); } int cnt=0; for(int i=1;i<=n;i++){ if(fa[i]==i) cnt++; } if(cnt==1) return true; else return false; } long long kruskal(){ int cnt=0; ans=0; for(int i=1;i<=n;i++) fa[i]=i; //初始化 sort(edges,edges+m); for(int i=0;i<m;i++){ int a=find(edges[i].u),b=find(edges[i].v); //并查集判断是否在一颗树上 if(a==b){ continue; } else{ merge(a,b); ans+=edges[i].w; cnt++; } if(cnt==n-1) return ans; } } int main(int argc, char** argv) { // freopen("testdata.txt","r",stdin); cin>>n>>m; int x,y,z; for(int i=0;i<m;i++){ cin>>x>>y>>z; edges[i].u=x; edges[i].v=y; edges[i].w=z; } if(!liantong()){ cout<<"orz"<<endl; return 0; } else{ ans=kruskal(); cout<<ans<<endl; } return 0; }
