cs231n学习笔记——lecture5 Convolutional Neural Network

该博客主要用于个人学习记录，部分内容参考自：超详细斯坦福CS231n课程笔记（第五课）——卷积神经网络、cs231n学习笔记——五.CNN 卷积神经网络

一、卷积神经网络的历史

二、卷积神经网络的结构

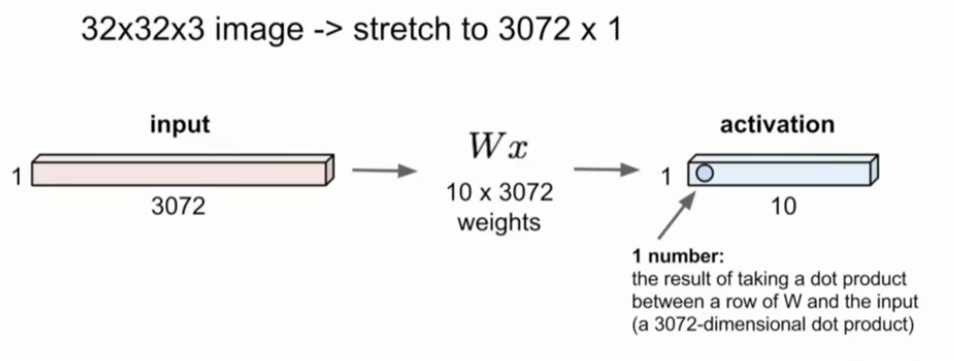
1、全连接层Fully Connected Layer

对于一张32×32×3的图像，将所有像素展开成一个3072维的向量，把向量和权重矩阵相乘，由此得到这一层的输出值。在本例中，我们用10行数据与这个3072维的数据进行点积运算，然后得到一个数字，就是该神经元的值，这个例子中应该有10个这样的值。但事实上这样就失去了像素数据之间的空间关系.

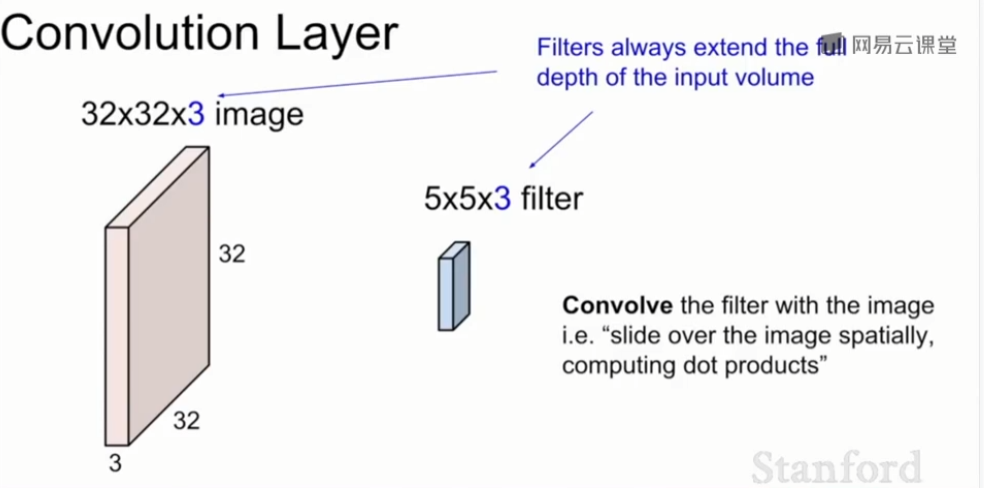
2、卷积层Convolution Layer

卷积层与全连接层的主要区别是，我们可以保全空间结构。
将5×5×3的卷积核在整个图像上滑动，计算出每一个空间定位时的点积结果。采用卷积核总是会将输入量扩展至整个卷积层，所以它们都是一个很小的空间区域，它们通常会遍历所有通道。我们采用这个卷积核和一个给定的空间区域，在这个卷积核和一块图像之间进行点积运算。

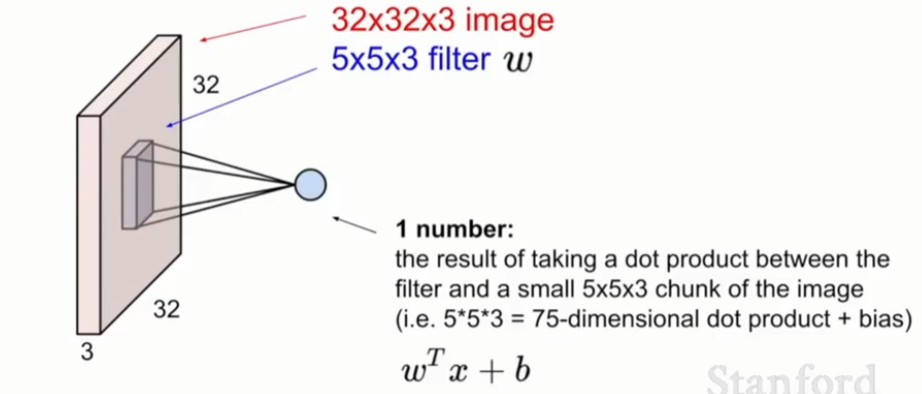
我们要做的就是在图像空间区域上覆盖这个卷积核，然后进行点积运算，也就是将卷积核每个位置元素和与之对应图像区域的像素值相乘，经过运算后得到一个结果，是\(W^Tx+b\)。在这个例子中，我们进行了5×5×3次点积运算，再加上偏置值，结果

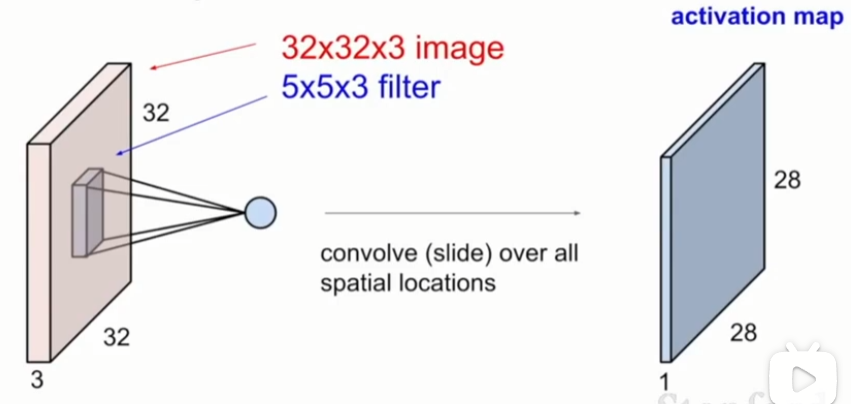
我们如何滑动卷积核并遍历所有空间位置呢？
将这个卷积核从左上方边角处开始，并让卷积核遍历输入的所有像素点 ，在每个位置我们都进行点积运算，每一次运算都会在输出激活映射（activation map）中产生一个值。之后再继续滑动。最简单的滑动方式就是一个像素一个像素滑动，直至填满输出激活映射。也可以每经过两个输入值进行一次滑动，也就是一次滑动两个像素点，这样会得到不同尺寸大小的输出。注意，在这里我们是32×32×3的输入，但输出却是28×28×1。输出的维度取决于你的滑动方式。

当我们在处理一个卷积层时，我们希望用到多种卷积核，因为每一个卷积核都可以从输入中得到一个特殊的模式或概念。所以我们会有一组卷积核，这里我们将用到图中绿色的卷积核，也是5×5×3的大小，将它滑动，遍历输入层的所有位置，然后得到了第二个相同尺寸的绿色的激活映射。

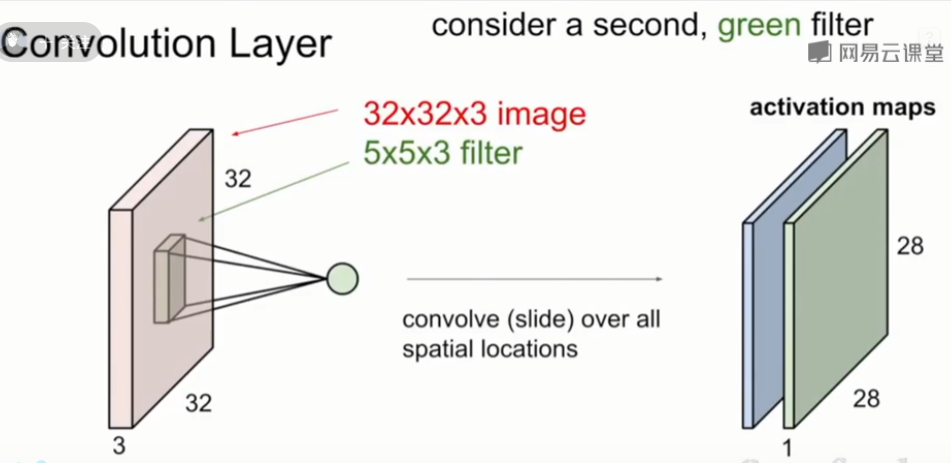
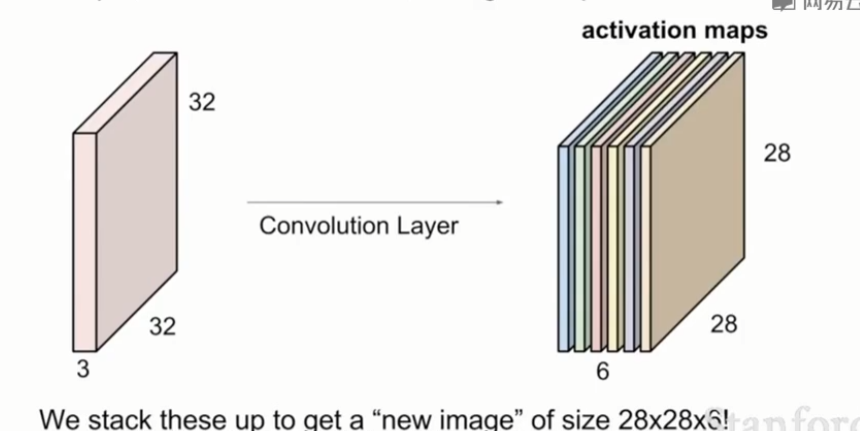
如果我们有6个卷积核，每个卷积核的大小都是5×5×3，这样我们就会得到一个六层的激活映射，也就是一个28×28×6的输出。

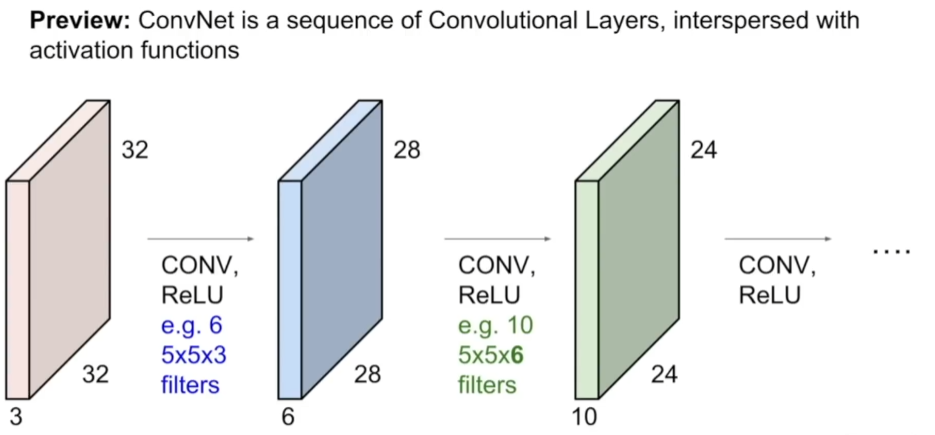
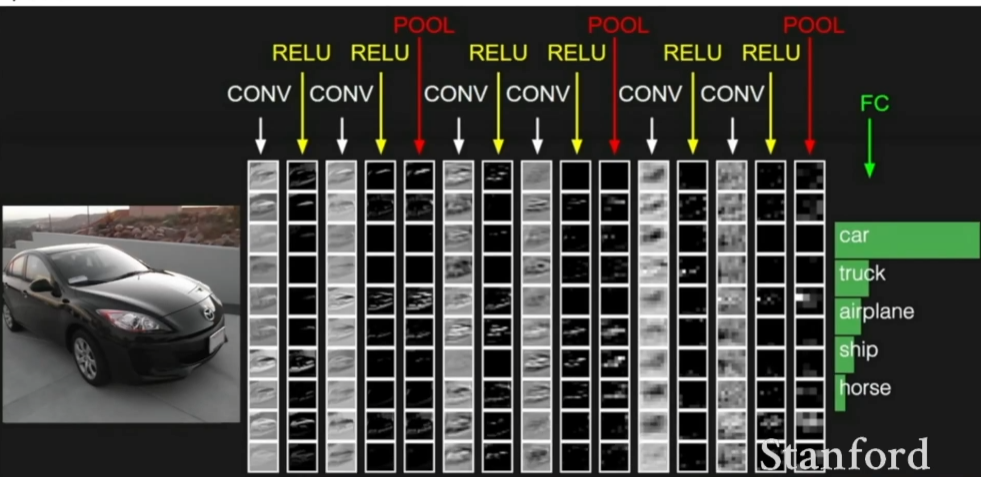
ConvNet基本上是由多个卷积层组成的一个序列，它们依次堆叠，然后用激活函数对其进行逐一处理，比如说一个ReLU激活函数；然后将得到一些比如Conv、ReLU、池化层。

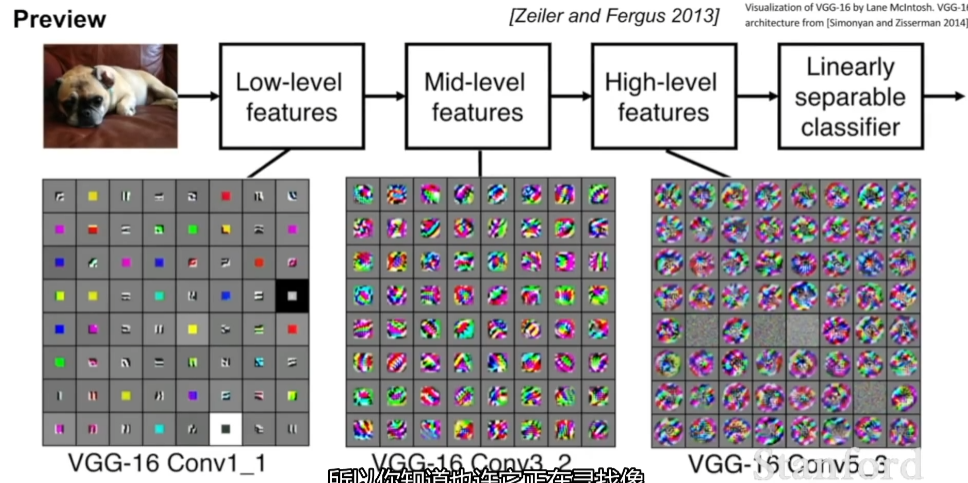
前面几层的卷积核一般代表了一些低阶的图像特征，比如说一些边缘特征；而对于中间层的卷积核，可以看到一些更复杂的图像特征，比如边角和斑点等；而后面的几层，会看到更加丰富的内容。

卷积神经网络整体上来看就是输入一个图片，让它通过很多层，比如卷积层、非线性层、池化层，经过这些处理后，最终得到卷积层输出，然后就可以用全连接层连接所有的卷积层输出，用其获得一个最终的分值函数。

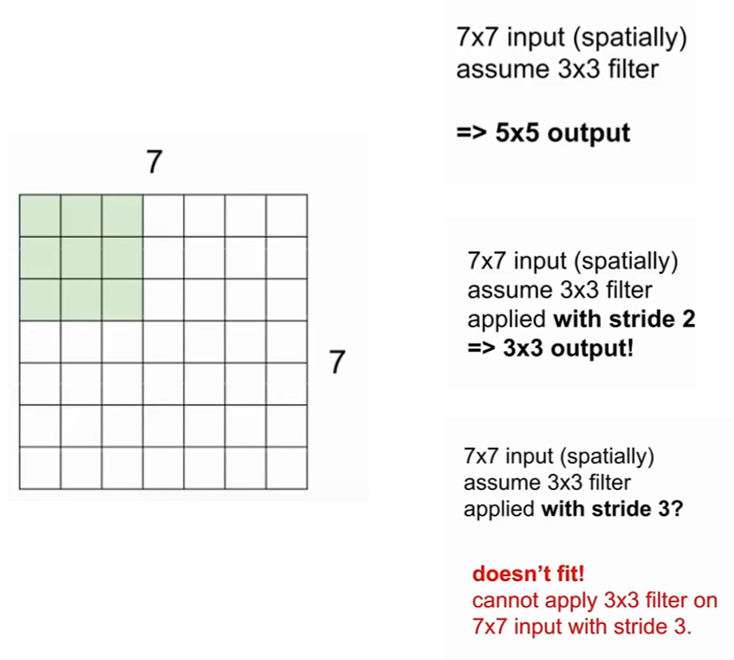
如何准确计算激活映射？
以7×7的输入和3×3的卷积核为例，若每次滑动的步数为1一个步长，最后将得到一个5×5的输出；若每次滑动2个步长，最后得到3×3的输出；若每次滑动3个步长，则会导致不对称输出，不采用。

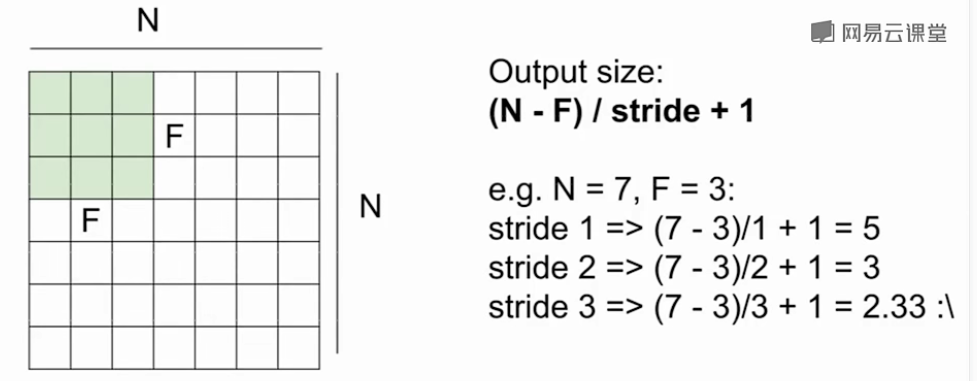
假设输入的维度为N，卷积核大小为F，滑动时的步幅为stride，最终每个输出的空间维度为\((N-F)/stride+1\)

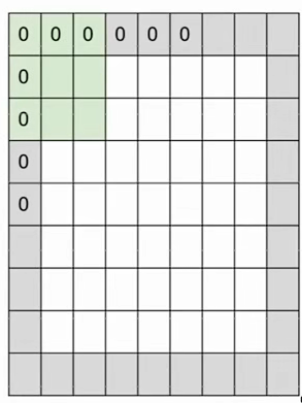
在实践中，会用0来填充输入图像（Zero Padding），设填充宽度为P, 则此时输出图像尺寸为\((N - F + 2P) / stride + 1\)

例题

假设输入图像为32×32×3，有10个5×5的卷积核，步长为1，填充宽度为2，则输出图像的尺寸是多少？

答：在每个边上增加宽度为2的填充，所以输入图像填充后变为32+2*2，利用公式，\((32+2*2-5)/1+1=32\)，所以对每个卷积核，我们的输出都是32×32，总共有10个卷积核，则输出图像的尺寸为32×32×10

在这一层中有多少个参数？

答：每个卷积核有\(5*5*3+1(偏差项)=76\)个参数，共有10个卷积核，所以这一层共有\(76*10=760\)个参数。

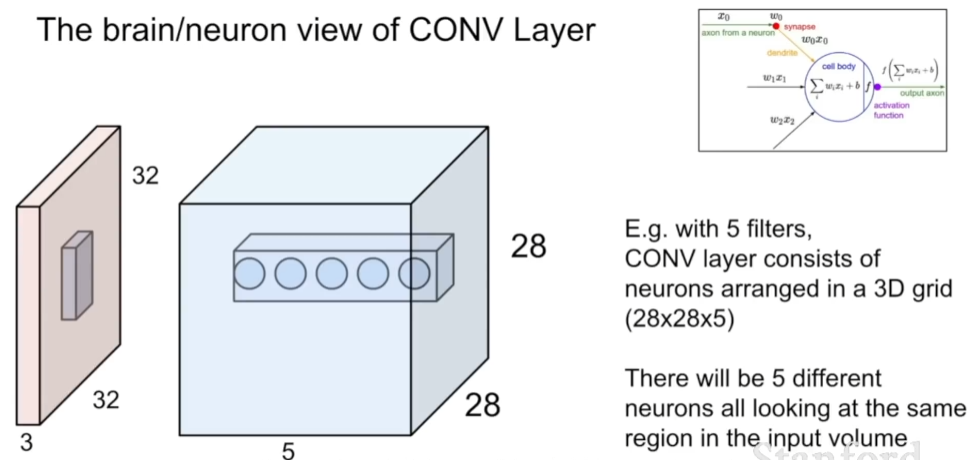
每隔几个卷积层就有一个池化层夹在中间

3、池化层Pooling Layer

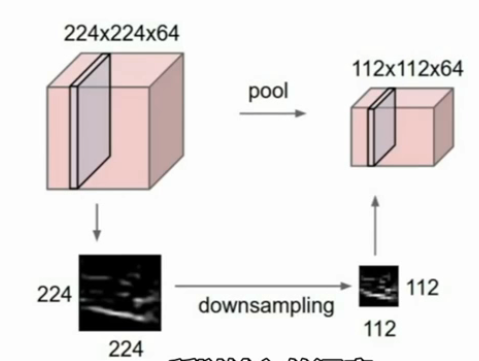
池化层主要是为了将之前层生成的表示更小，越小最后得到的参数越数量少，也关系到给定区域内的不变性问题。池化层所要做的是降低采样率的处理，例如对于224×224×64的输入进行空间上的降采样处理，所以最后得到的是一个112×112的结果，重要的一点是，我们不会在深度方向上做池化处理，而是只做平面上的，所以输入的深度和输出的深度是一样的。

最常见的方法是最大池化层，例如下面的例子中，池化层也有一个卷积核的大小，且卷积核的大小和我们所要池化处理的区域大小是相同的，假设我们使用2×2的filter，且设定步长为2，让这个卷积核滑过整个输入部分，取滑过区域中的最大值。

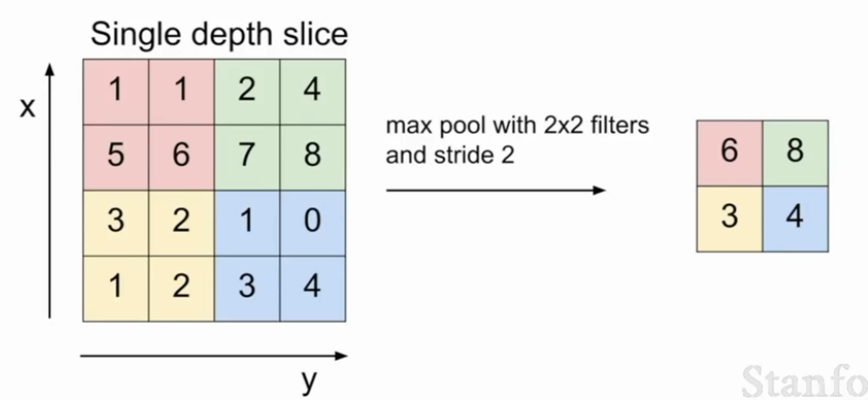
问：为什么是最大池化而不是均值池化？
答：其实每个局部区域中的每一个值都是经过激励函数产生的值，它体现了这个局部的某一特种，我们就拿这个局部特征最明显的那个作为这个局部的代表就可以了。

问： 既然设定步长和池化都能做降采样，能否只用步长不用池化或者只用池化而不用步长？
答：可以这么做，确实在工业界有人这么做。

三、总结

• 卷积网络的工作原理，怎么把卷积核池化层堆叠起来，最后怎么与全连接层结合；

• 小尺寸卷积核和更深的网络结构是一个趋势；

• 完全弃用池化和全连接层，而只保留卷积层形成深层卷积网络也是一个趋势；

• 典型的结构：卷积ReLU重复N次，每次做一个池化，如此反复，最后来到全连接ReLU层，最后用softmax得到你的类别分数。