cs231n学习笔记——Lecture 4 Backpropagation and Neural Networks

该博客主要用于个人学习记录，部分内容参考自：【cs231n】详解神经网络中的反向传播、CS231n笔记三：神经网络之反向传播、超详细斯坦福CS231n课程笔记（第四课）——反向传播和神经网络

一、反向传播backpropagation

反向传播是链式法则的递归调用

(一)反向传播backpropagation

例子1

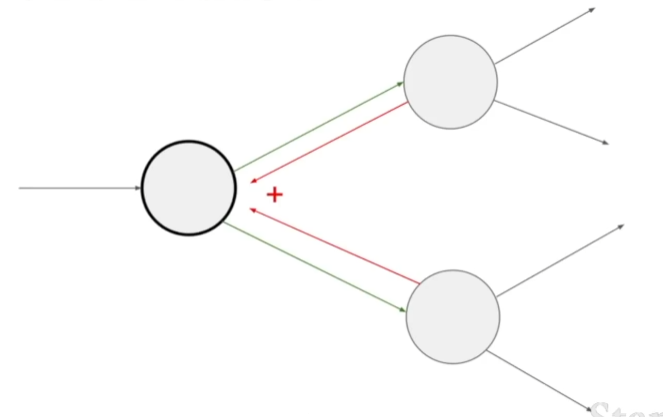
图中绿色的值是传入的参数值和计算图向前计算得到的值，红色值是利用计算图反向计算时得到的梯度值

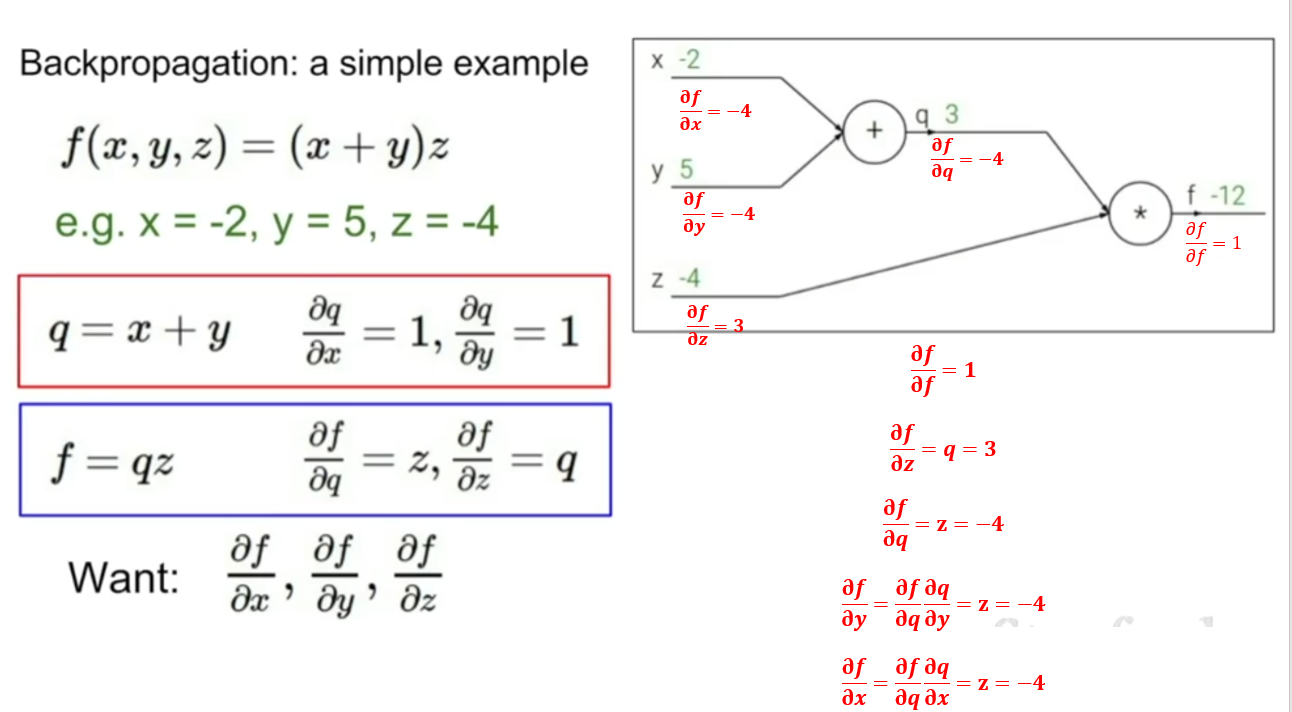
  • 向前传播计算中间变量的梯度
  • 从后往前，根据链式法则和向前传播得到的中间梯度计算梯度

节点

对于一个节点，计算本地梯度并存储跟踪下来，在反向传播的时候接受从上游传回来的梯度值，直接用这个梯度值乘以本地梯度然后得到需要传回前一个连接点的值【local gradient × upstream gradient】，在下一个节点进行传播时，不用考虑除了直接相连的节点之外的任何东西。

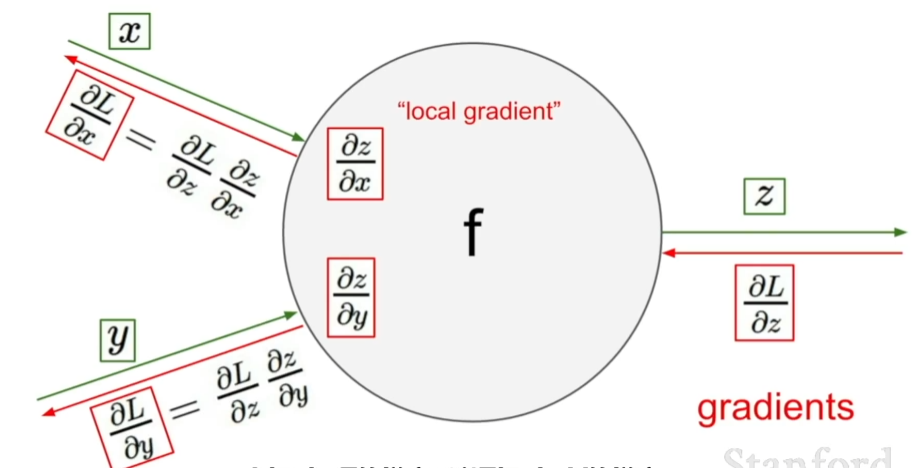
在这个图中，x和y是前面的节点传入该节点的值，z是节点的输出值，进行反向传播时，从输出方向传入上游的梯度值，我们只需要将在向前传播过程中计算好的梯度值（即本地梯度）和从上游传过来的梯度值利用链式法则相乘即可得到我们想要的结果，再将这个结果传入到前面的直接相连的节点中去。

例子2

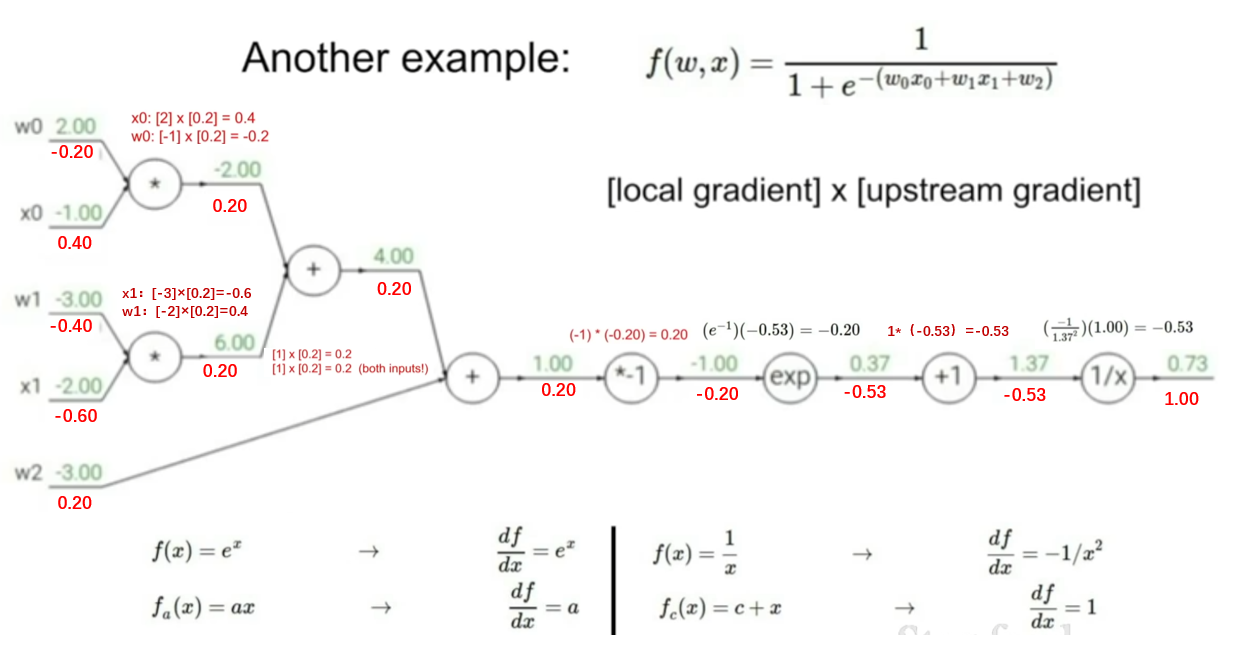
  • 节点\(\frac{1}{x}\)

    • 上游传过来的梯度值upstream gradient：\(\frac{df}{df}=1\)
    • 本地梯度表达式：\(f(x)=\frac{1}{x} → \frac{df}{dx}=-\frac{1}{x^2}\)
    • x的值：1.37
    • 本地梯度值：\(-\frac{1}{1.37^2} = -0.53\)
    • 利用链式法则求得最终值为：\(-0.53×1=-0.53\)

  • 节点\(+1\)

    • 上游传过来的梯度值upstream gradient：-0.53
    • 本地梯度表达式：\(f(x)=x+c → \frac{df}{dx}=1\)
    • x的值：0.37
    • 本地梯度值：1
    • 利用链式法则求得最终值为：\(1×-0.53=-0.53\)

  • 节点\(exp\)

    • 上游传过来的梯度值upstream gradient：-0.53
    • 本地梯度表达式：\(f(x)=e^x → \frac{df}{dx}=e^x\)
    • x的值：-1.00
    • 本地梯度值：\(e^{-1}\)
    • 利用链式法则求得最终值为：\(e^{-1}×{-0.53}=-0.20\)

  • 节点\(*\)

    • 上游传过来的梯度值upstream gradient：0.20
    • 本地梯度表达式：\(f(x)=xy → \frac{df}{dx}=y\)
    • \(x_0=-1.00\) → 本地梯度值为\(w_0=2.00\)
    • \(w_0=2.00\) → 本地梯度值为\(x_0=-1.00\)
    • 利用链式法则求得最终值为：\(w_0\)为-0.20，\(x_0\)为0.40

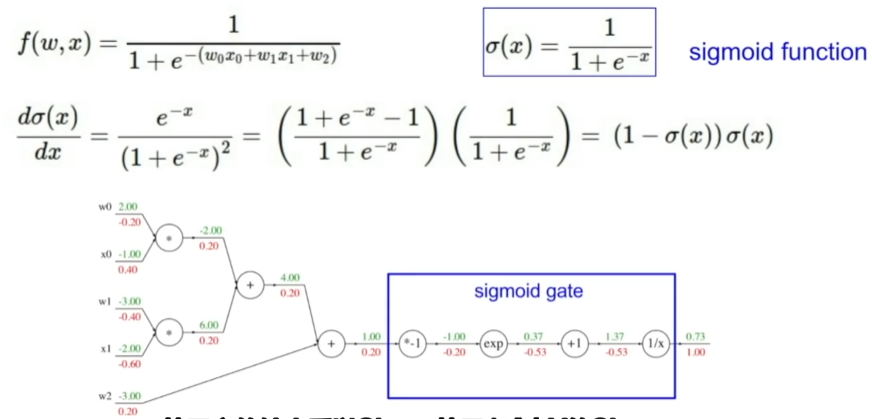
  • 将上图中几个简单的节点用一个大节点替换
    sigmoid函数： \(\sigma(x)=\frac{1}{1+e^{-x}}\) → \(\frac{d\sigma(x) }{dx}=(1-\sigma(x))\sigma(x)\)

patterns in backward flow

  • 加法门Add gate: gradient distributor，获取上游梯度，不改变任何值，传递分发给相连的分支；
  • Max门Max gate: gradient router，对大的那个输入的本地梯度是1，对小的输入的本地梯度是0，相当于将上游输入的梯度进行了一个路由选择；
  • 乘法门Mul gate: gradient switcher，对输入x的本地梯度是输入y的值，对输入y的本地梯度是输入x的值，相当于进行了交换。
  • Copy gate: gradient adder

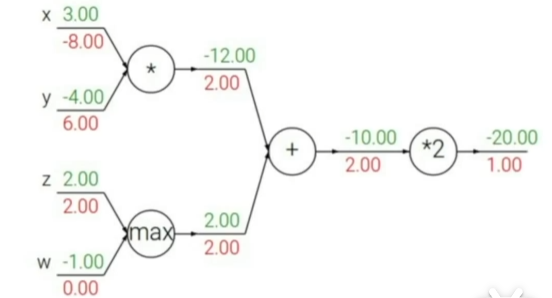
gradients add at branches

在反向传播过程中，当涉及多个上游节点的梯度汇聚到同一个下游节点时，需要将所有上游节点的梯度相加作为这个本地节点的总上游梯度。这可以解释为：因为在前向传播计算函数值时，这个本地节点的取值会影响与之相连的之后所有节点，因而在反向传播的过程中，之后所有节点的梯度也都会反过来影响这个本地节点的梯度取值。

（二）高维矩阵反向传播

雅可比矩阵Jacobian matrix

  • 雅克比矩阵是函数的一阶偏导数以一定方式排列成的矩阵。雅克比矩阵每一行都是偏导数，矩阵中的每一个元素都是输出向量的每个元素对输入向量每个元素分别求偏导的结果。
  • 对于一个4096维向量输入和一个4096维向量输出，所需要的雅克比矩阵的大小为4096*4096，实际中我们进行小批量处理，那么就意味着这个矩阵将会更大，比如一次进行100个样本的处理，那么雅克比矩阵就会变成409600 * 409600。如果这样的话，将会计算很慢，甚至说不可计算。
  • 由于输入的第一个元素和输出的第一个元素有关系，所以实际上我们算出的雅克比矩阵是一个对角矩阵，所以不需要把整个矩阵都算出来。

例子

假设X是2维向量，W是2*2矩阵
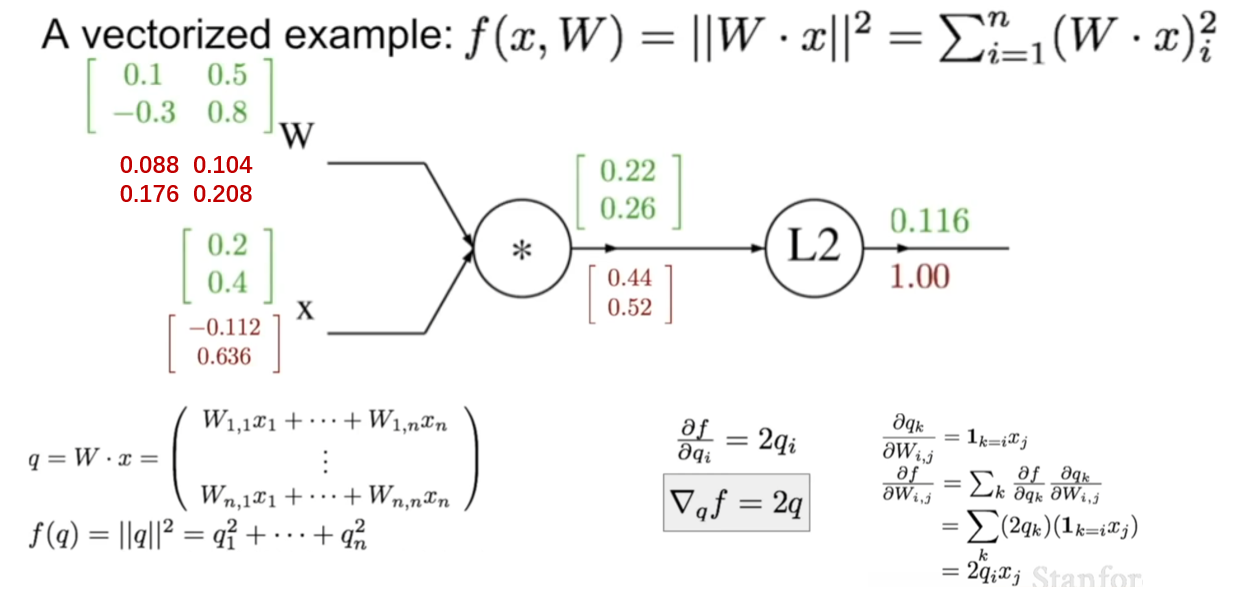
image
image
每个变量的梯度的维度应当和这个变量的维度保持一致。

（三）模块化设计

前向传播和反向传播API

  • 在forward()中：我们计算所有操作的结果并保存所有中间变量，以便在之后计算梯度时使用；
  • 在backward()中：需要应用链式法则，从最后一个节点开始反向计算，最终得到函数对于所有输入变量的梯度。
class ComputationalGraph(object):
  #...
  def forward(inputs):
    # 1. pass inputs to input gates...
    # 2. forward the computational graph:
    for gate in self.graph.nodes_topologically_sorted():
      gate.forward()
     return loss # the final gate in the graph outputs the loss
  def backward():
for gate in reversed(self.graph.nodes_topologically_sorted()):
  gate.backward()
  return inputs_gradients

以乘法门为例

  • 在forward()中：计算乘法结果z，同时还需要保存self.x和self.y，以便在后续计算梯度时使用，最终返回计算结果z;
  • 在backward()中：输入为dL/dz（用dz表示），期望输出dL/dx和dL/dy（分别用dx和dy表示），应用链式法则可以通过已知的dz和之前保存的self.x和self.y来计算dx和dy。
class ComputationalGraph(object):
  #...
  def forward(x,y):
  	z = x * y
  	self.x = x
  	self.y = y
  	return z
  def backward(dz):
	dx = self.y * dz
	dy = self.x * dz
	return [dx , dy]

二、神经网络 Neural Network

在此前我们已经使用了很多这种分数函数：\(f=W·x\)
现在使用一个2层的神经网络：\(f=W_2max(0,W_1x)\)
或者使用一个3层的神经网络：\(f=W_3max(0,W_2max(0,W_1x))\)
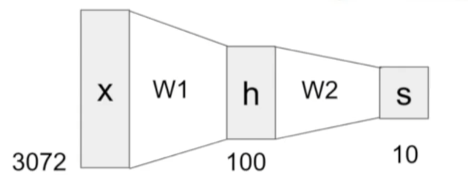
image

  • 神经网络以分层的方式堆叠一些简单的函数，以构成更复杂的非线性函数。

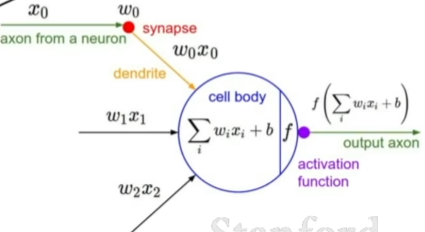
image

  • 计算图里的节点相互连接，我们需要输入“信号x”，所有x的输入量比如x0、x1、x2等，采用比如赋予权重W的方法，叠加汇合到一起，将结果整合起来后得到一个激活函数，将激活函数应用在神经元的端部，得到的值作为输出。

  • 几种常用的激活函数
    image

  • 两层神经网络也可以叫单隐藏层网络，三层神经网络也是双隐藏层网络
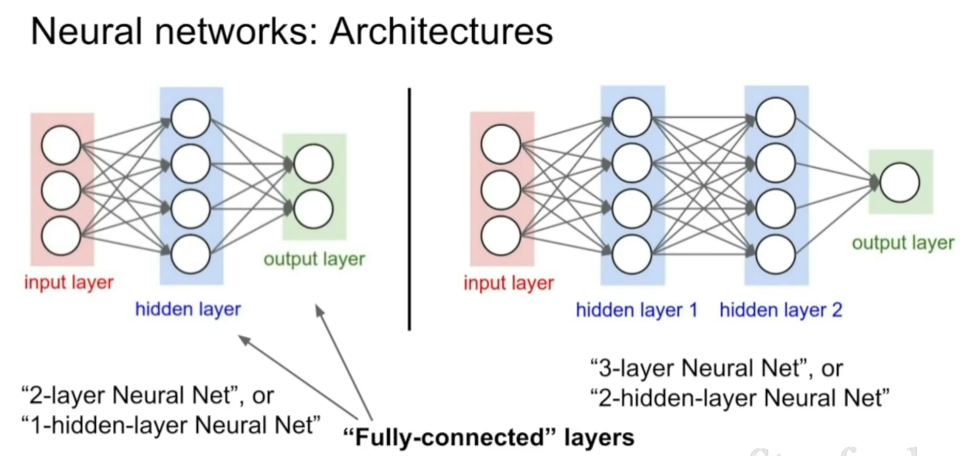
    image
    image

  • 神经网络可以近似任何连续函数
posted @ 2022-12-02 11:45  jasf  阅读(231)  评论(0)  编辑  收藏  举报