Redis 中 HyperLogLog 讲解
是什么
作用
- 估计集合的基数（去重元素个数）
- [a,b,c,d] 的基数是 4
- [a,b,c,d,a] 的基数还是 4
原理
- 概率论的伯努利实验 + 修正
-
让我们玩一个游戏
- 你来掷硬币，我来猜你掷了多少回合
- 每回合规定，直到掷出反面结束，否则一直掷
- 比如你可以一直掷正面，不结束该回合
- 也可能第一次就是反面，回合结束
- 我需要的唯一信息
- 你掷硬币次数最多的回合，掷了多少次硬币
-
答案很简单
-
若你最多掷了n次，则你掷了 (1 << n)个回合
-
可参考论文数学证明
-
基于正反1/2的假设
- 掷1次概率 1/2
- 掷2次概率 1/2 * 1/2
- 掷3次概率 1/2 * 1/2 * 1/2
- ......
- 掷n次概率 1/ (1 << n)
因为我们可以猜测你大概玩了(1 << n)个回合
-
-
-
这个游戏大致描述了算法的思想
具体的原理详见论文
-
LogLog算法原型
问题
获取一个任意元素集合的基数
前提
- 用64位哈希值作为元素的唯一指代，哈希值中的01出现的概率各为1/2
- 哈希值的二进制01串，表示硬币的正面反面，我们从头开始数，直到1结束，找到000...1的长度
- 00001011010... 长度为5
- 10101010000... 长度为1
- ......
- 为了准确性，我们分布式的玩掷硬币游戏，元素被哈希到多个阵营，分别玩掷硬币游戏
- 统计各个阵营基数的和，作为总体的基数
解决步骤
-
64位哈希值分为，14位找哈希桶，50位找000...1的长度
-
14位找哈希桶，共有 (1 << 14) 个哈希桶
-
50位找000...1的长度，最长是50，我们把各个桶000...1的长度的最大值存下来
-
(1 << 6) - 1 = 63 > 50，所以每个桶最少用6位即可存下来最长长度
-
(1 << 14) * 6 / 8 / 1024 = 12K，共占用12K内存，分布如下
第0组 第1组 .... 第16383组 [000 000] [000 000] [000 000] [000 000] .... [000 000] -
比如
- 处理 01001001010001 00100010010001111...
- 前14位 01001001010001 大小为 4689，因此在第4689组
- 后50位一开始000...1的长度为3，后面的即可忽略不计，因此第4689组值为000011 = 3
- 处理 01001001010001 00001001010011101...
- 前14位 01001001010001 大小为 4689，因此也在第4689组
- 后50位一开始000...1的长度为5，比3大，因此第4689组值更改为000101 = 5
- 处理 01001001010001 10001001010011101...
- 前14位 01001001010001 大小为 4689，因此还在第4689组
- 后50位一开始000...1的长度为1，比5小，不处理
- 处理 01001001010001 00100010010001111...
-
-
将所有的元素的哈希值按照如上处理
-
假设每个哈希桶存的值为R，那么该桶的基数大致为 (1 << R)
-
所有桶的基数和为 ∑(1 << R)
-
为减少误差，若桶数为m，实际使用 m * (1 << R0) ，其中R0为R的平均值
-
为进一步减少误差，常添加一个常数修正，故最终表达式为：
HyperLogLog优化
调和平均数
-
原因
算数平均数，易受到极端值的影响
-
调整后
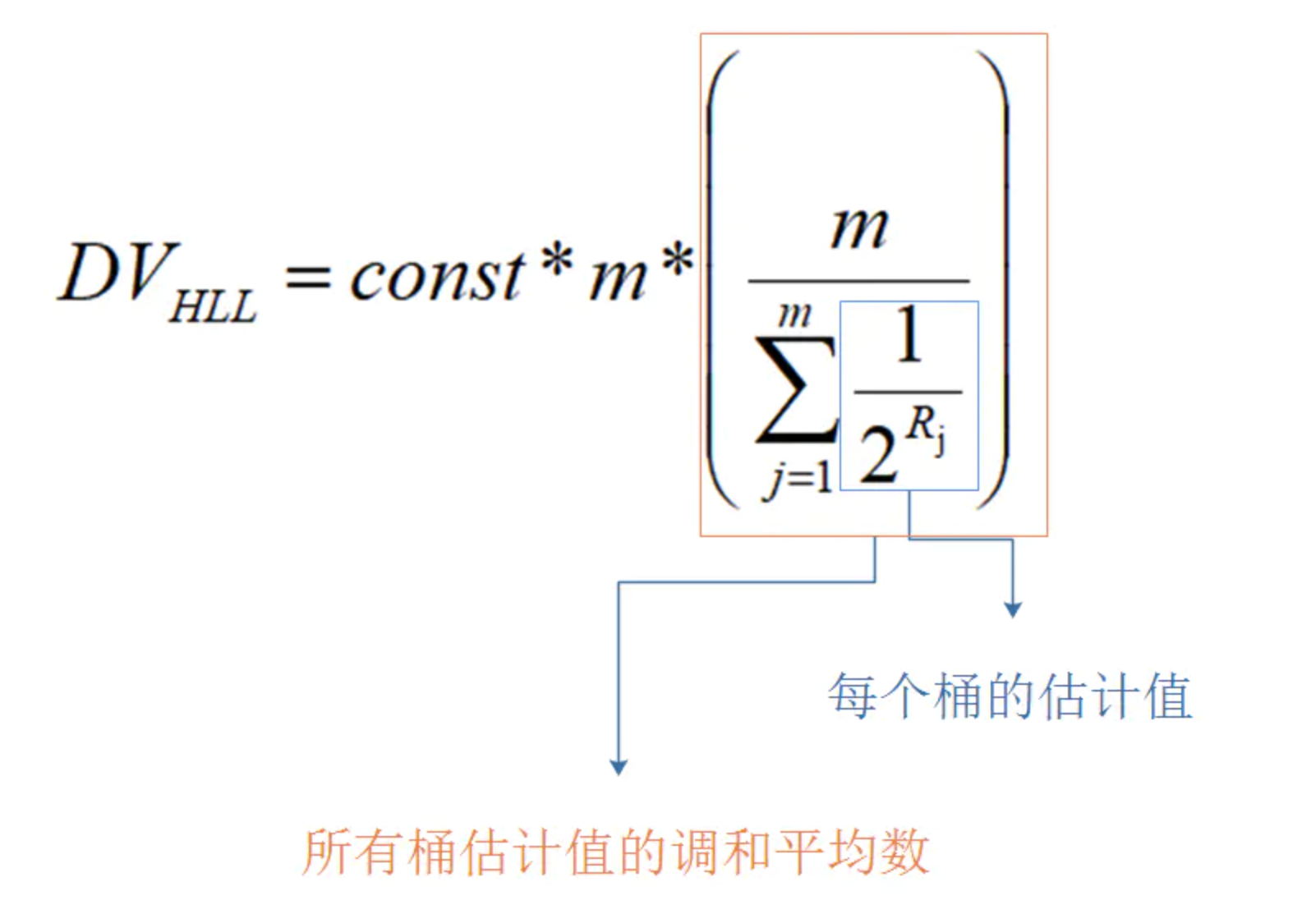
数据量小时
此时由概率论方法统计误差较大，修正为
// m 为桶数
// V 为结果为0的桶的个数
if (DV < (5 / 2) * m && V != 0) {
DV = m * log(m/V)
}
常数的选择
若m为桶数，定义p
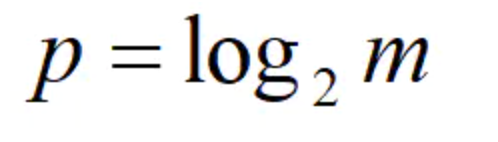
Constant 为
switch (p) {
case 4: constant = 0.673 * m * m;
case 5: constant = 0.697 * m * m;
case 6: constant = 0.709 * m * m;
default: constant = (0.7213 / (1 + 1.079 / m)) * m * m;
}
