maxHBLT的合并&初始化&时间复杂度分析

1. 定义

[extened binary tree] 扩充二叉树是有 external node (用来代替空子树, 也就是 nullptr) 的 binary tree. 对应地, 其他 nodes 叫 internal node.
\(s(x)\) 是从 node x 到其 子树的 external node 的左右路径中最短的一条.
- If x is an external node, \(s(x)=0\) .
- If x is an internal node, \(s(x)=\min\{s(LeftChild),s(RightChild)\}+1\) .
更直观的说法是, \(s(x)\) 就是从以 x 为 root 的最高 complete binary tree 的层数.
[HBLT] 当且仅当一颗 binary tree 的任何一个 internal node 的 \(s(LeftChild)\) 都大于或等于 \(s(RightChild)\), 这颗 binary tree 被称为 height-biased lefist tree (HBLT).
[WBLT] 设 \(w(x)\) 表示 node x 所有 descendent node 的数量, 则当且仅当一颗 binary tree 的任何一个 internal node 的 \(w(LeftChild)\) 都大于或等于 \(w(RightChild)\), 这颗 binary tree 被称为 weight-biased lefist tree (HBLT).
[max(min) HBLT] HBLT + max(min) tree.
[max(min) WBLT] WBLT + max(min) tree.

2. 性质

令 x is an interal node of an HBLT:

以 x 为 root 的 (sub)tree 的节点数量至少为 \(2^{s(x)}-1\) .

证明:
根据 定义 1.2 , 由于到达 external node 的最短路径为 \(s(x)\) , 因此在自 x 向下一直到第 \(s(x)-1\) 层都无 external node;
也就是说, 自该层向上到 x 是一棵 complete binary tree.
根据 Binary_Tree 的性质 2.2, 以 x 为 root 的 (sub)tree 至少包含上述 complete binary tree 的 \(2^{s(x)}-1\) 个节点.
而再往下的层就不能确定节点的数量了.
若以 x 为 root 的 (sub)tree 有 m 个节点, 那么 \(s(x)\) 至多为 \(\log_{2}{(m+1)}\) .
从 x 到一个 external node 的最右路径 (即从 x 开始延 Right Child 移动的路径) 的长度为 \(s(x)\) .

3. max HBLT 的合并

3.1. 合并逻辑分析

合并两棵 max HBLT 最好用递归完成.
下图展示了 max HBLT 的合并过程.

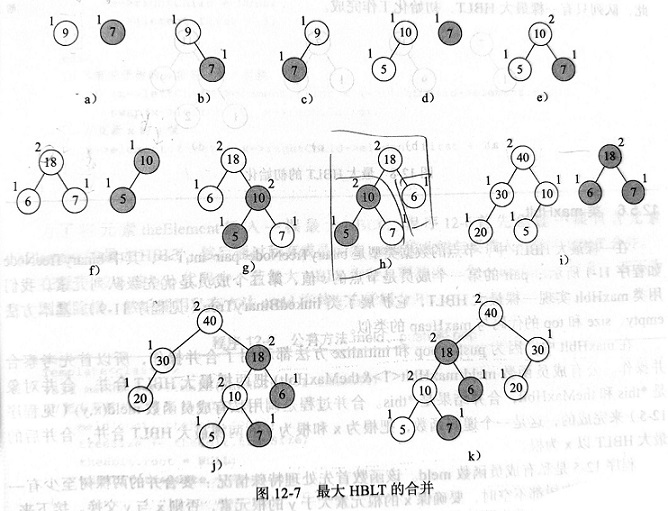
(a) 中 9 与 7 合并, 总是将右合并至左 (左的根理所应当更大);
递归进入 9 的 RightChild, 由于是 nullptr, 直接用 7 取代之.
(b) 展现了合并结果.
由于 9 的 \(s(LeftChild) = 0 < s(RightChild) = 1\), 需要交换其左右子树.
(c) 展现了交换完的最终结果.
(d) 中以 10 和 7 为根的左右 subtree 合并, 总是将右合并至左 (左的根理所应当更大);
递归进入 10 的 RightChild, 由于是由于是 nullptr, 直接用 7 取代之.
(e) 展现了合并结果.
由于 10 的 \(s(LeftChild) = 1 = s(RightChild) = 1\), 无需交换其左右子树.
因此 (e) 即为最终结果.
(f) 中以 18 和 10 为 root 的左右 subtree 合并, 总是将右合并至左 (左的根理所应当更大);
递归进入 18 的 RightChild = 7, 由于不是 nullptr, 比较 7 与 10 的大小, 发现 7 不能做 root;
交换 18->RghtChild 这根指针与 10 的 root 这根指针 (也就是说交换完成后, 18 -> RightChild 应该是以 10 为根的 subtree, 而原本的 7 成为了右边的待合并树).
交换完成后, 在调用函数迭代, 实际上就是 2 中 (d) 和 (e) 的问题.
(g) 是内层函数合并完的结果.
再次比较 6 与 10 的 s 值, 进行适当的交换.
....

3.2. 代码实现

将上面的逻辑具体实现为代码并不容易,
因此添加了大量注释帮助理解.
先写一个私有方法实现递归.

// Private method.
template<class T>
void maxHBLT<T>::m_meld(binaryTreeNode<std::pair<int, T>>*& x,
                        binaryTreeNode<std::pair<int, T>>*& y)
{
    if (y == nullptr) { return; }
    // When {x} is the rightest external node, replace {x=nullptr} with {y}.
    if (x == nullptr) {
        x = y; // meld
        return;
    }

    // Make sure meld tree with smaller root to the one with a larger.
    // Notice that {std::swap(ptr_1,ptr_2)} exchanges the content in two addresses.
    // The result is that PARENT of x points to the same address with different content (of y), same to y.
    if (x->element.second < y->element.second) { std::swap(x, y); }

    // Suppose that "m_meld(x->rightChild, y)" can meld the subtree
    // whose root is"x->rightChild" with whose is "y".
    m_meld(x->rightChild, y);

    // After right subtree of 'x' is melded with tree 'y',
    // following code adjests the tree whose root is "x" to an HBLT.
    if (x->leftChild == nullptr) {
        /*******************
        *   9          9   *
        *    \   ->   /    *
        *     7      7     *
        ********************/
        // "std::swap()" costs 3 steps, but here we only spends 2 steps.
        x->leftChild = x->rightChild;
        x->rightChild = nullptr;

        // Reset the value of "s(x)".
        x->element.first = 1;
    } else {
        /**********************
        *   9             9   *
        *  / \     ->    / \  *
        * 7   8         8   7 *
        *    / \       / \    *
        *   6   4     6   4   *
        ***********************/
        // Make sure the "s(x->leftChild)" is larger than "s(x->rightChild)".
        if (x->leftChild->element.first < x->rightChild->element.first) {
            // If not smaller, exchange "x->leftChild" and "x->rightChild".
            std::swap(x->leftChild, x->rightChild);
            // Reset the value of "s(x)".
            x->element.first = x->rightChild->element.first + 1;
        }
    }
}

用共有方法封装一下作为对外部的接口.

// Public method.
template<class T>
void maxHBLT<T>::meld(maxHBLT<T>& theHblt)
{
    m_meld(root, theHblt.root);
    treeSize += theHblt.treeSize;
    theHblt.root = nullptr;
    theHblt.size = 0;
}

3.3. 时间复杂度分析

假设合并两棵树 x 与 y, 它们的元素个数分别为 \(m\) 与 \(n\);
pravate 方法 m_meld 仅沿着 x 和 y 的左/右子树移动, 因此复杂度为:

\[O(s(x)+s(y)) \]

其中 \(s(x)\) 和 \(s(y)\) 的最大值分别为 \(\log_{2}{(m+1)}\) 和 \(\log_{2}{(n+1)}\)
因此时间复杂度进一步推导为:

\[O(\log{m}+\log{n})=O(\log{(mn)}) \]

4. max HBLT 的初始化

4.1. 逻辑实现

将所有元素分别单独创建为只有一个元素的 max HBLT, 然后全部 push 入一个 FIFO 队列内部.
然后利用循环, 每次从队首 pop 两个 max HBLT 出来 meld, 然后将结果 push 入队尾;
直到只剩一个合并完的 max HBLT.

4.2. 代码实现

template<class T>
void maxHBLT<T>::initialize(T* theElement, int theSize)
{
    arrayQueue<binaryTreeNode<std::pair<int, T>>*> q(theSize);
    erase();
    for (int i = 1; i <= theSize; i++) {
        q.push(new binaryTreeNode<std::pair<int, T>>(std::pair<int, T>(1, theElement[i])));
    }
    for (int i = 1; i <= theSize; i++) {
        binaryTreeNode<std::pair<int, T>>* b = q.front();
        q.pop();
        binaryTreeNode<std::pair<int, T>>* c = q.front();
        q.pop();
        m_meld(b, c);
        q.push(b);
    }
    if (theSize > 0) {
        root = q.front;
    }
    treeSize = theSize;
}

4.3. 时间复杂度分析

假设用 \(n\) 个元素初始化一棵 max HBLT, 同时为了简单起见, 假设 \(n\) 是 2 的幂次方.
根据 4.1 的分析:

第一轮 pop 后, 合并了 \(n/2\) 对元素个数为 \(1\) 的 max HBLT.
第二轮 pop 后, 合并了 \(n/4\) 对元素个数为 \(2\) 的 max HBLT.
第三轮 pop 后, 合并了 \(n/8\) 对元素个数为 \(4\) 的 max HBLT.
...
第 \(n/2\) 轮 pop 后, 合并了 \(1\) 对元素个数为 \(n/2\) 的 max HBLT.

若两颗棵 max HBLT 的元素个数都为 \(i\); 根据 3.3 的时间复杂度分析, private 方法 m_meld 合并这两棵树的最大步数 (完全遍历 + 左树 nullptr 的一次检测) 为:

\[i+i+1=2i+1 \]

因此 initialize 的时间复杂度为:

\[O((2*1+1) * n/2 + (2*2+1)* n/4 + (2*4+1)*n/8 + \cdots )=O(n\sum{\frac{2i+1}{2^i}})=O(n) \]

Reference & picture resource | Data Structures, Algoritms, and Applications in C++, Sartaj Sahni

posted @ 2022-08-05 22:58 JamesNULLiu 阅读(119) 评论(0) 编辑收藏举报

刷新页面返回顶部

jamesnulliu