AVL Tree (1) - Definition, find and Rotation

1. 定义

(15-1) [AVL tree]:
1. 一棵空二叉树是 AVL tree;
2. 若 T 是一棵非空二叉树, 则 T 满足以下两个条件时, T 是一棵 AVL tree:
  - T_LeftSubtree 和 T_RightSubtree 是 AVL tree.
  - \(| h_{Left} - h_{Right}| \leq 1\).
[AVL search tree]: AVL tree + binary search tree.
AVL tree 的高度 \(h=O(\log{n})\)
[balance foctor] 平衡因子可能取值为 -1, 0, 1;
对于 node x, \(bf(x)\) 定义为: \(h_{x\_LeftSubtree} - h_{x\_RightSubtree}\).

AVL Tree 的宗旨在于使 BST 保持平衡, 进而避免 BST 过度倾斜 (极端情况下 BST 有可能成为链表) .

2. btNode 和 AVLTree 的定义

<utility> 头文件提供了 std::pair 的定义, 便于使用融合 key 类型和 value 类型的复合类型.
<iostream> 头文件提供的输出方法由 private method preOrder 使用, 以测试代码正确性.

Click to show the codes

// AVL Tree

#include <utility>
#include <iostream>

/**
 * @brief Binary tree node.
 * @tparam T Should be std::pair<Key_Type, Element_Type> in binary search tree.
*/
template<class T>
struct btNode
{
    T data;
    btNode<T>* left, * right;
    // Constructor for btNode.
    btNode(T d = {}, btNode<T>* l = nullptr, btNode<T>* r = nullptr) :
        data(d), left(l), right(r) {}
};

template<class K, class E>
class AVLTree
{
public:
    // Constructor for AVLTree.
    AVLTree() :root(nullptr) {}
    // @brief PreOrder ouput.
    void preOrder() { preOrder(this->root); }

public:
    // @brief Find the node with key {tKey} and return its address.
    btNode<std::pair<K, E>>* find(const K& theKey) const;
    // @brief [Iteration] Create a node with {tPair} and insert it to the tree.
    void insert_I(const std::pair<K, E>& tPair);
    // @brief [Recursion] Create a node with {tPair} and invoke method {m_insert_R}.
    void insert_R(const std::pair<K, E>& tPair);
    // @brief [Iteration] Erase the node with key {tKey}.
    void erase_I(const K& tKey);
    // @brief [Recursion] Erase the node with key {tKey}.
    void erase_R(const K& tKey);

private: // Rotate methods.
    // @brief Right rotate subtree whose root is {tRoot}, return {tRoot->left} as new root.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = rightRotate(parentTarget->left)
    inline btNode<std::pair<K, E>>* rightRotate(btNode<std::pair<K, E>>* tRoot);
    // @brief Left rotate subtree whose root is {tRoot}, return {tRoot->right} as new root.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = leftRotate(parentTarget->left);
    inline btNode<std::pair<K, E>>* leftRotate(btNode<std::pair<K, E>>* tRoot);
    // @brief For LL case, right rotate subtree {tRoot}, return {tRoot->left} as new root.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = llRotation(parentTarget->left);
    inline btNode<std::pair<K, E>>* llRotation(btNode<std::pair<K, E>>* tRoot);
    // @brief For RR case, left rotate subtree {tRoot}, return {tRoot->left} as new root.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = rrRotation(parentTarget->left);
    inline btNode<std::pair<K, E>>* rrRotation(btNode<std::pair<K, E>>* tRoot);
    // @brief For LR case, left rotate {tRoot->left}, right rotate {tRoot}, return {tRoot->left->right}.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = lrRotation(parentTarget->left);
    inline btNode<std::pair<K, E>>* lrRotation(btNode<std::pair<K, E>>* tRoot);
    // @brief For RL case, right rotate {tRoot->right}, left rotate {tRoot}, return {tRoot->right->left}.
    // e.g. To rotate {parentTarget->left} : parentTarget->left = rlRotation(parentTarget->left);
    inline btNode<std::pair<K, E>>* rlRoattion(btNode<std::pair<K, E>>* tRoot);
    
private:
    // @brief Private recurse method to insert.
    btNode<std::pair<K, E>>* m_insert_R(btNode<std::pair<K, E>>* tRoot, btNode<std::pair<K, E>>* tNode);
    // @brief Private recurse method to erase.
    btNode<std::pair<K, E>>* m_erase_R(btNode<std::pair<K, E>>* tRoot, const K& tKey);
    // @brief Private recurse method for preorder output.
    void preOrder(btNode<std::pair<K, E>>* tRoot);
private:
    btNode<std::pair<K, E>>* root;
};

template<class K, class E>
void AVLTree<K, E>::preOrder(btNode<std::pair<K, E>>* tRoot)
{
    if (!tRoot) return;
    std::cout << tRoot->data.second;
    preOrder(tRoot->left);
    preOrder(tRoot->right);
}

3. Find

解释可以参照 BST 的 find 方法.

Click to show the codes

// @brief Find the node with key {tKey} and return its address.
template<class K, class E>
btNode<std::pair<K, E>>* AVLTree<K, E>::find(const K& theKey) const
{
    // {keyNode} traverse the tree, searching for matched node.
    btNode<std::pair<K, E>>* keyNode = root;
    // Iteration ends if {keyNode} is nullptr.
    while (keyNode) {
        if (theKey < keyNode->data.first) {
            keyNode = keyNode->left;
        } else if (theKey > keyNode->element.first) {
            keyNode = keyNode->right;
        }
        // ELSE: {keyNode->data.first} equals {tKey}.
        else {
            return keyNode;
        }
    }
    // No matching pair.
    return nullptr;
}

4. Left Rotate & Right Rotate

在探讨何时要旋转以及如何旋转之前, 我们不妨先实现两个单纯的左右旋转方法.

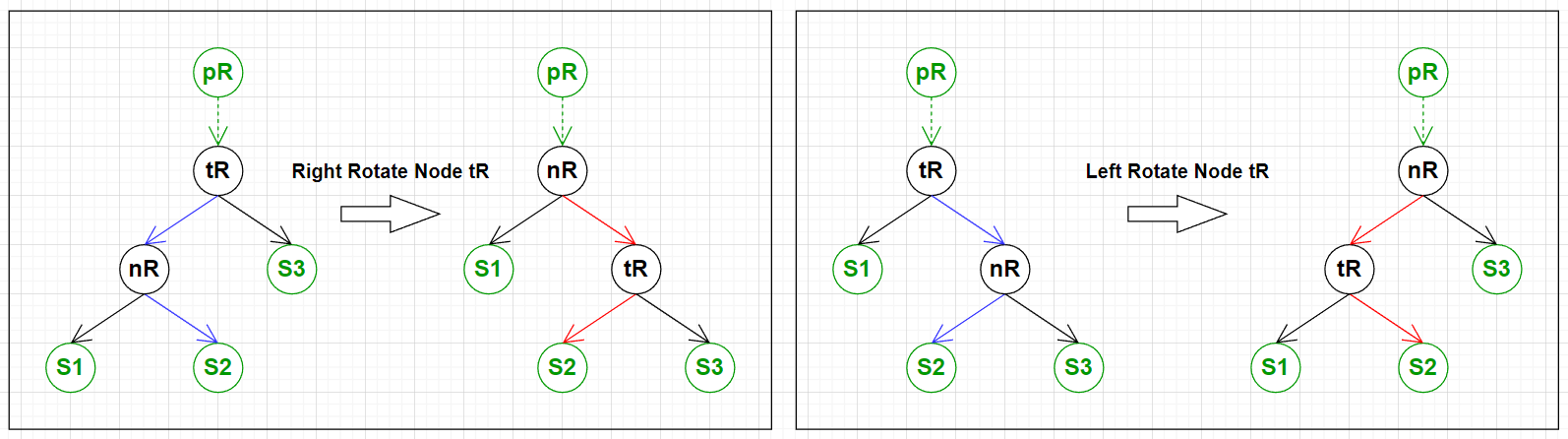
上图中左边是向右旋转 rightRotate , 右边是向左旋转 leftRotate .
很直观, 也没什么好多说的, 上代码.

Click to show the codes

// @brief Right rotate subtree whose root is {tRoot}, return {tRoot->left} as new root.
// e.g. To rotate {parentTarget->left} : parentTarget->left = rightRotate(parentTarget->left)
template<class K, class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::rightRotate(btNode<std::pair<K, E>>* tRoot)
{
    btNode<std::pair<K, E>>* new_tRoot = tRoot->left;
    tRoot->left = new_tRoot->right;
    new_tRoot->right = tRoot;
    return new_tRoot;
}

// @brief Left rotate subtree whose root is {tRoot}, return {tRoot->right} as new root.
// e.g. To rotate {parentTarget->left} : parentTarget->left = leftRotate(parentTarget->left)
template<class K, class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::leftRotate(btNode<std::pair<K, E>>* tRoot)
{
    btNode<std::pair<K, E>>* new_tRoot = tRoot->right;
    tRoot->right = new_tRoot->left;
    new_tRoot->left = tRoot;
    return new_tRoot;
}

5. 4 Cases for Rotation

AVL Tree 保持平衡的方法是计算 balance factor 后进行旋转.
下面四张图展示了需要旋转的 4 种情况以及旋转的方式.

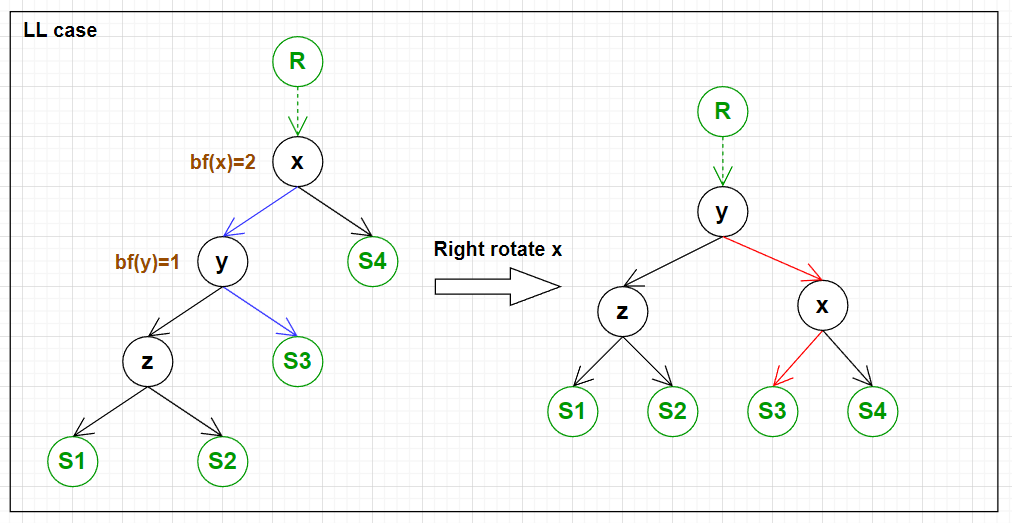
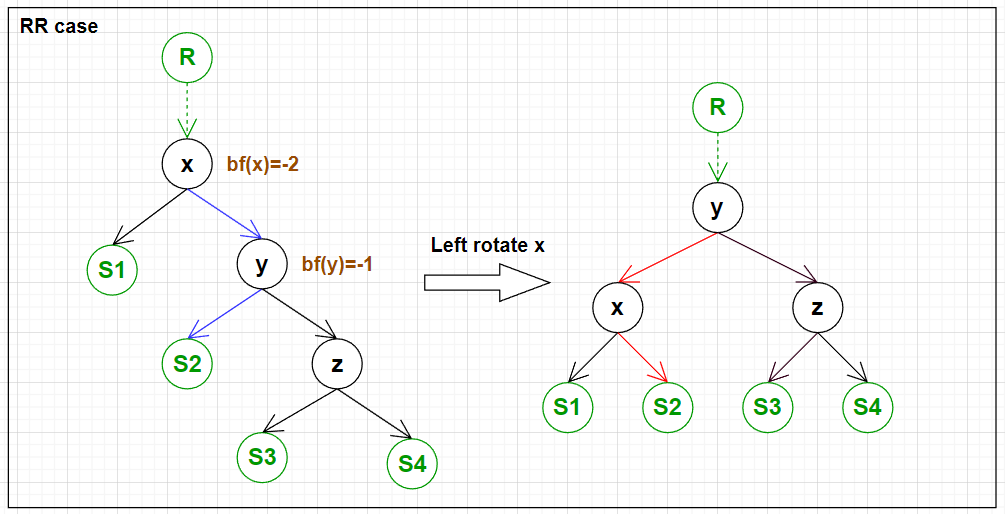
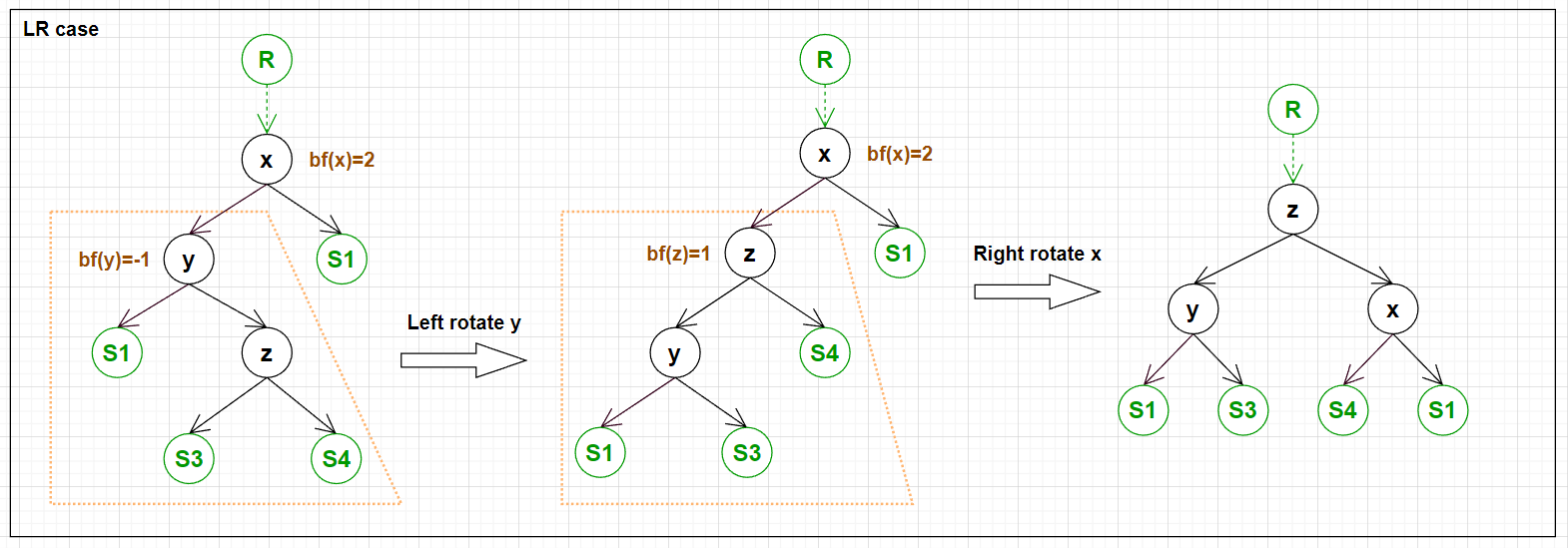
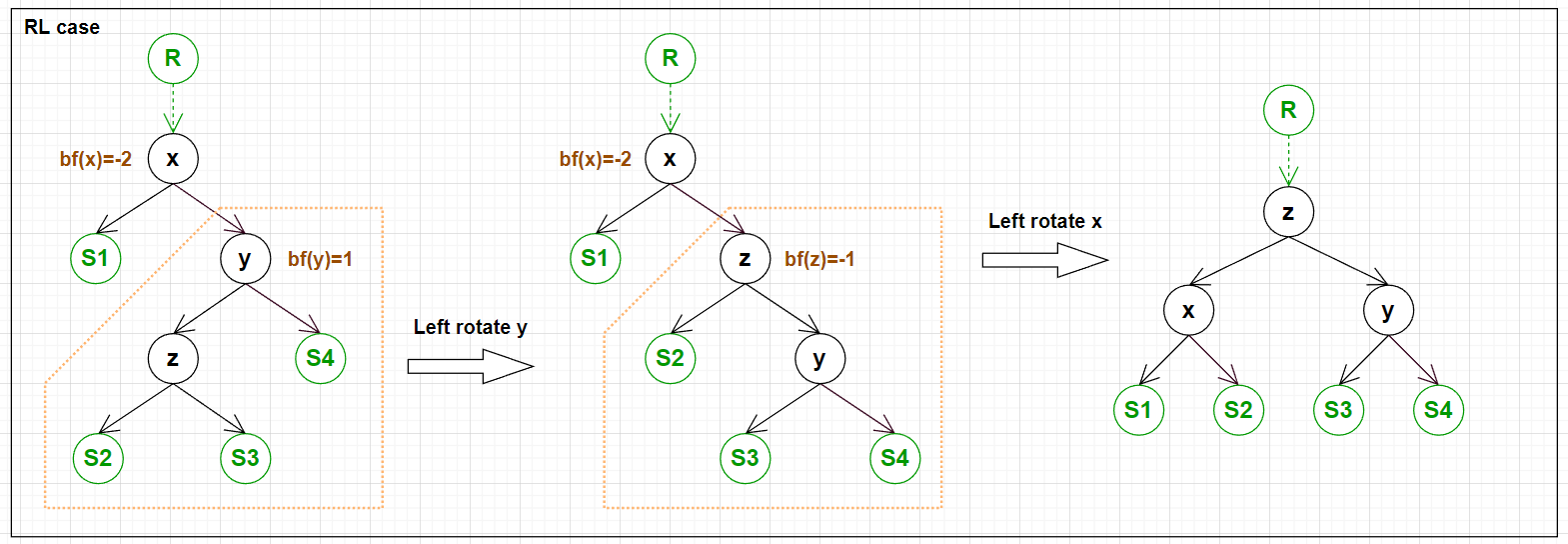
实现四种情况的旋转的代码:

Click to show the codes

// @brief For LL case, right rotate subtree {tRoot}, return {tRoot->left} as new root.
// e.g. To rotate {parentTarget->left} : parentTarget->left = llRotation(parentTarget->left);
template<class K, class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::llRotation(btNode<std::pair<K, E>>* tRoot)
{
    return rightRotate(tRoot);
}

// @brief For LL case, left rotate subtree {tRoot}, return {tRoot->left} as new root.
// e.g. To rotate {parentTarget->left} : parentTarget->left = rrRotation(parentTarget->left);
template<class K, class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::rrRotation(btNode<std::pair<K, E>>* tRoot)
{
    return leftRotate(tRoot);
}

// @brief For LR case, left rotate {tRoot->left}, right rotate {tRoot}, return {tRoot->left->right}.
// e.g. To rotate {parentTarget->left} : parentTarget->left = lrRotation(parentTarget->left);
template<class K, class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::lrRotation(btNode<std::pair<K, E>>* tRoot)
{
    tRoot->left = leftRotate(tRoot->left);
    return rightRotate(tRoot);
}

// @brief For RL case, right rotate {tRoot->right}, left rotate {tRoot}, return {tRoot->right->left}.
// e.g. To rotate {parentTarget->left} : parentTarget->left = rlRotation(parentTarget->left);
template<class K,class E>
inline btNode<std::pair<K, E>>* AVLTree<K, E>::rlRoattion(btNode<std::pair<K, E>>* tRoot)
{
    tRoot->right = rightRotate(tRoot->right);
    return leftRotate(tRoot);
}

Reference |
(1) Data Structures, Algoritms, and Applications in C++, Sartaj Sahni
(2) AVL Tree | Set 1 (Insertion), princiraj1992, rathbhupendra, Akanksha_Rai, sohamshinde04, nocturnalstoryteller, rdtank, kaiwenzheng644, hardikkoriintern

posted @ 2022-08-16 23:09 JamesNULLiu 阅读(26) 评论(0) 编辑收藏举报

刷新页面返回顶部

jamesnulliu

AVL Tree (1) - Definition, find and Rotation

1. 定义

2. btNode 和 AVLTree 的定义

3. Find

4. Left Rotate & Right Rotate

5. 4 Cases for Rotation

公告