言简意赅的 Kahn 和 DFS 拓扑排序 (C++实现)

I 邻接表 (Adjacent List) 实现有向图

在类内定义结构体 Vertex (顶点).

Vertex 包含三个成员 :

• data 表示某顶点内所存放的内容, 类型由模板决定 (默认char)
• indegree 表示某顶点的入度, 即有向图中有多少条边以该顶点为终点
• adjList 表示某顶点的邻接表, 即以该顶点为起点接出的所有边 (edge) 的终点的下标 (下标表示一个顶点在内存中存放的位置, 也就是说稍后会用数组存放所有顶点)

adjList 用 std::list 实现. 对每个顶点来说, 我们并不关注其接出的边的先后顺序. 由于可能的添加/删除边操作较多, 使用链表实现的容器存放目标顶点的下标是合理的.

数据成员

Graph 中唯一定义数据成员 vert_vec, 容器为 std::vector.
vert_vec 存放了有向图中所有的顶点.

举例

若有 Graph 实例 g;
g 中存放了两个顶点, 数据依次为 A 和 B, B 接出一条边至 A, 则有:

• g.vert_vec[0].data 为 A, g.vert_vec[1].data 为 B;
• g.vert_vec[0].indegree 为 1, g.vert_vec[1].indegree 为 0;
• g.vert_vec[0].adjList 为空, g.vert_vec[1].adjList 为 {(Index)0} // A 在 vert_vec 中的下标

其他函数

1. vertNum() 返回顶点个数.

   STL 容器的 size() 函数的返回值类型为 size_t , 即 unsigned long long. 一般在实现小型算法时我们会强制转换成无符号类型以保留负数区间.

2. addEdge() 接收两个下标参数, 创建由前者 sbjVert_I 对应顶点连向后者 objVert_I 对应顶点的边;
   具体操作是在 sbjVert_I 对应的 adjList // 邻接表 容器中任意位置插入 objVert_I (也就是下标数值);
   然后将 bjVert_I 对应的 indegree 增加 1 (因为连向它的边增加了一根).

3. setVert() 就是根据传入下标和数值设置某个顶点的 data.

C++ 实现

template<class _Elem = char>
class Graph
{
public: // Interface
    using Index = long long;
    using Sizet = long long;
    struct Vertex { _Elem data; Sizet indegree; list<Index> adjList; };
    Graph(Sizet vertNum) : vert_vec(vertNum, Vertex {{},0,{}}) {
    }
    constexpr Sizet vertNum() const { 
        return (Sizet)vert_vec.size(); 
    }
    constexpr void addEdge(Index sbjVert_I, Index objVert_I) {
        vert_vec[sbjVert_I].adjList.push_back(objVert_I);
        ++(vert_vec[objVert_I].indegree);
    }
    constexpr void setData(Index vertI, const _Elem& data) {
        vert_vec[vertI].data = data;
    }
    bool topologicalSorting_Kahn(queue<_Elem>& result) { return solution_Kahn(result); }
    bool topologicalSorting_DFS(stack<_Elem>& result) { return solution_DFS(result); }
private:
    bool solution_Kahn(queue<_Elem>& result);
    bool solution_DFS(stack<_Elem>& result);
    void visit_DFS(Index vertI, stack<_Elem>& result,
                vector<bool>& isAdded2Result,
                vector<bool>& isUnderRecursion);
private: // Data Member
    vector<Vertex> vert_vec;
};

II 拓扑排序 (Topological Sorting)

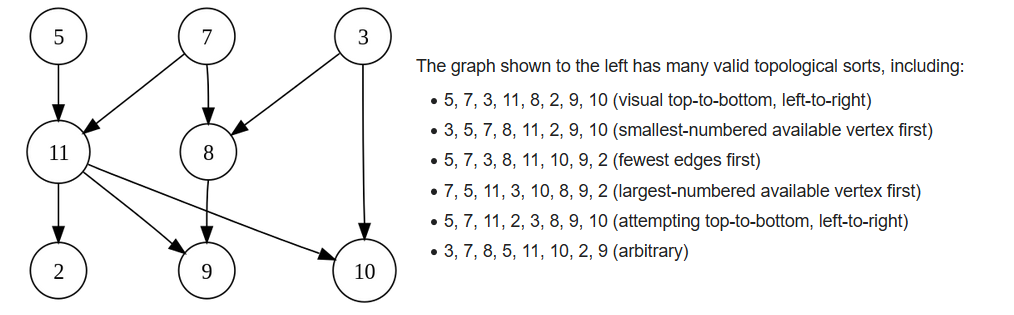
简单来说就是将有向图按边的方向排序, 保证任意顶点始终在其所有连接的终点 (如果存在) 的左边.
显而易见, 排序结果不一定唯一.
比如:
A -> B, A -> C
排序结果既可以是 A, B, C, 也可以是 A, C, B
当出现循环, 例如 A -> B, B -> A, 排序是不可能实现的;
因此拓扑排序的一个问题之一就是判断出循环.

III Kahn 算法

流程

建议结合代码看.

1. 定义两个线性容器 result 和 zeroIndegreeVertI;
   result 存放排好序的顶点的 data (或者也可以存放顶点下标);
   zeroIndegreeVertI 存放所有入度 (indegree) 为 0 的顶点的下标.
2. 先遍历一遍 vert_vec, 即存放了所有结点的数组.
   找到所有入度为 0 的结点, 将它们的的下标存放入 zeroIndegreeVertI 中.
3. 当 zeroIndegreeVertI 不为空, 循环执行以下操作
   a. 从 zeroIndegreeVertI 中取出一个顶点下标 (zeroIndegreeVertI 不再包含被取出的顶点下标).
   b. 遍历被取出的下标对应顶点的邻接表, 将表中指向的所有顶点的入度减 1; 如果某个顶点的入度减 1 后变为 0, 则将该顶点的下标存放入zeroIndegreeVertI.

C++ 实现

bool Graph::solution_Kahn(queue<_Elem>& result) {
    result = {};
    queue<Index> zeroIndegreeVertI_que; // Index of vertex with zero indegree
    for(Index i = 0; i < vertNum(); ++i) {
        if(vert_vec[i].indegree == 0) { zeroIndegreeVertI_que.push(i); }
    }
    while(!zeroIndegreeVertI_que.empty()) {
        Index curVertI = zeroIndegreeVertI_que.front(); zeroIndegreeVertI_que.pop();
        result.push(vert_vec[curVertI].data);
        for(Index linked_I : vert_vec[curVertI].adjList) {
            --(vert_vec[linked_I].indegree);
            if(vert_vec[linked_I].indegree == 0) { zeroIndegreeVertI_que.push(linked_I); }
        }
    }
    if(result.size() == vert_vec.size()) return true; // The graph is DAG.
    else return false; // There is at least one circle.
}

IV DFS 算法

流程

先将所有顶点表记为 Is-Not-Added-to-Result 和 Is-Not-Under-Recursion.
再将所有被标记为未被添加入结果的顶点调用递归函数 visit_DFS(), 伪代码如下:
----- Persudocode of visit_DFS(Vertex n) -----

if n is marked Is-Added-to-Result
	reutrn
if n is marked Is-Under-Recursion
	stop // There must be at least one circle!
mark n Is-Under-Recursion
for each vertex m in adjacent list of n
	visit_DFS(m)
mark n Is-Not-Under-Recursion
add data of n to result
mark n Is-Added-to-Result

递归只可意会不可言传(不是懒得写了)

C++ 实现

bool Graph::solution_DFS(stack<_Elem>& result) {
    result = {};
    vector<bool> isAdded2Result(vertNum(), false);
    vector<bool> isUnderRecursion(vertNum(), false);
    try {
        for(Index i = 0; i < vertNum(); ++i) {
            if(isAdded2Result[i] == false) { visit_DFS(i, result, isAdded2Result, isUnderRecursion); }
        }
    } catch(int status) { if(status == 1) { result = {}; return false; } }
    return true;
}
void Graph::visit_DFS(Index vertI, stack<_Elem>& result,
                vector<bool>& isAdded2Result,
                vector<bool>& isUnderRecursion) {
    if(isAdded2Result[vertI] == true) return;
    if(isUnderRecursion[vertI] == true) throw 1;
    isUnderRecursion[vertI] = true;
    for(Index linkedI : vert_vec[vertI].adjList) {
        visit_DFS(linkedI, result, isAdded2Result, isUnderRecursion);
    }
    isUnderRecursion[vertI] = false;
    result.push(vert_vec[vertI].data);
    isAdded2Result[vertI] = true;
}