阿基米德：抛物线求积

前言

​ 最近在读《微积分的力量》，书中讲到了阿基米德（Archimedes）的《抛物线求积法》（"Quadrature of the Parabola"）描述了阿基米德如何求解抛物线与直线围成的抛物线弓形的面积。解决这一问题的关键点是证明每个新构建三角形的面积都是上一层级三角形面积的1/8，可是作者省略了这部分的证明过程，只交代了后面无穷级数的计算方法。研究了一会没有任何头绪，好巧的是在油管上找到了相关证明的视频。由于是全英文视频，不是一篇正规的文章，所以字幕比较口语化，翻译起来也很困难，终于今天算是完成了，写篇文章总结一下。

​ 这是他的视频地址：Archimedes: Quadrature of the Parabola，有条件的朋友可以去看看。

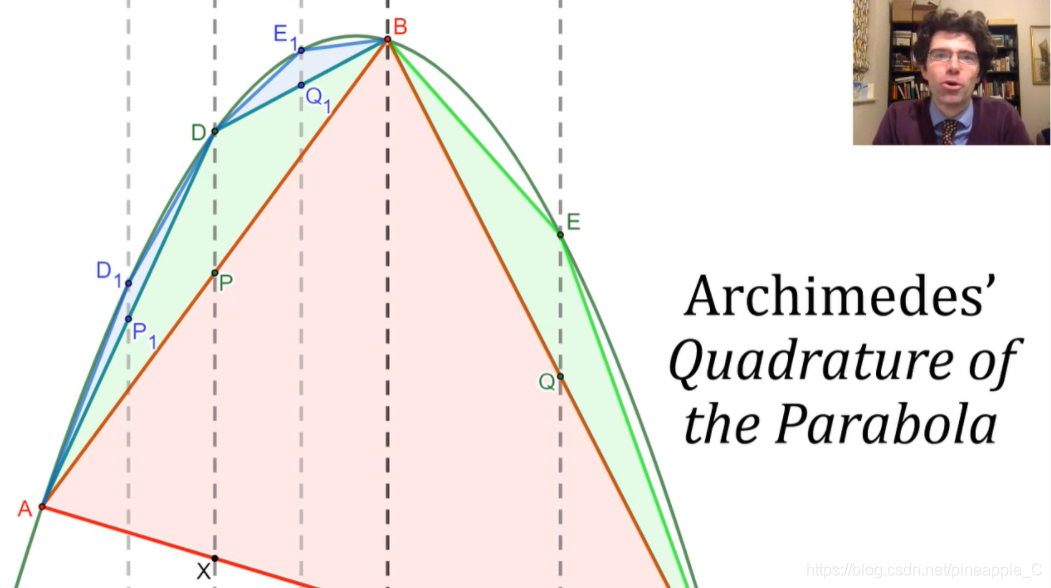
抛物线的秘密

​ 抛物线从哪来？

​ 取一个圆锥（corn），用一把刀🔪平行于锥体地面截切，会得到一个圆，如图：

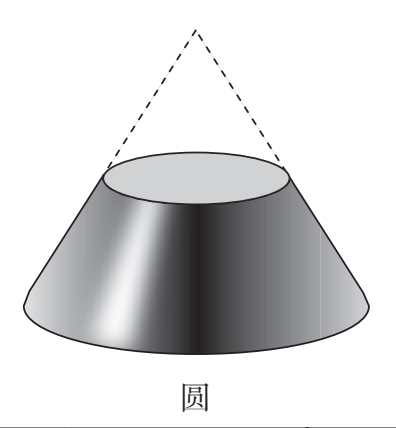
​ 如果它截切的角度略微倾斜，就会得到一个椭圆，如图：

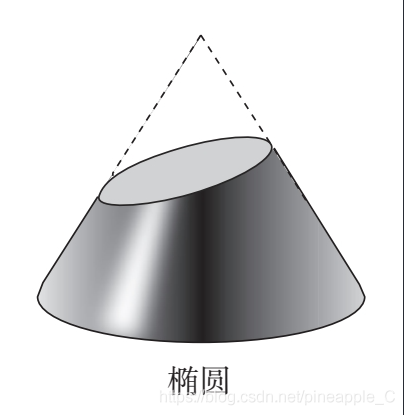
​ 如果它截切的角度与锥体的斜率相同，就会得到一条抛物线（parabola），如图：

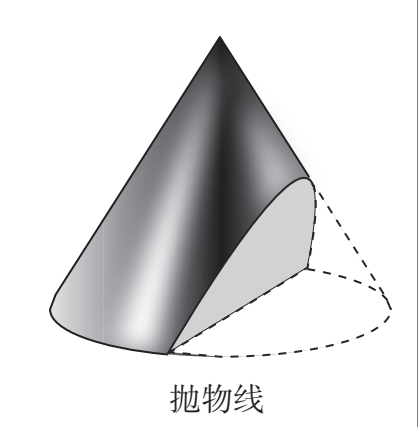
​ 抛物线是一个优美的轴对称图形，在它的顶点竖直向下做一条直线，就可以得到它的对称轴（axis of symmetry）：

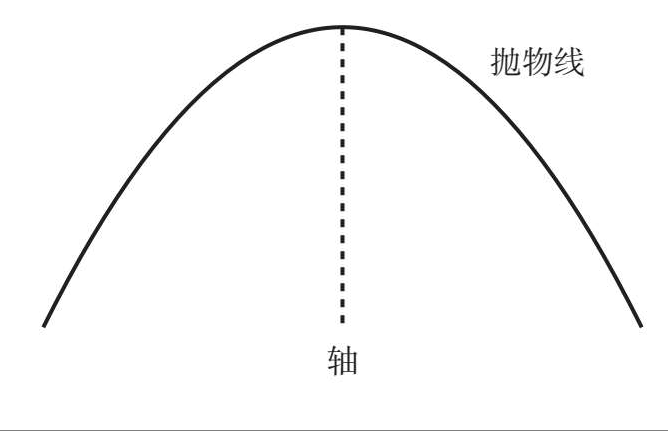
​ 而《抛物线求积法》中的积指的就是抛物线与一条直线围成的抛物线弓形面积：

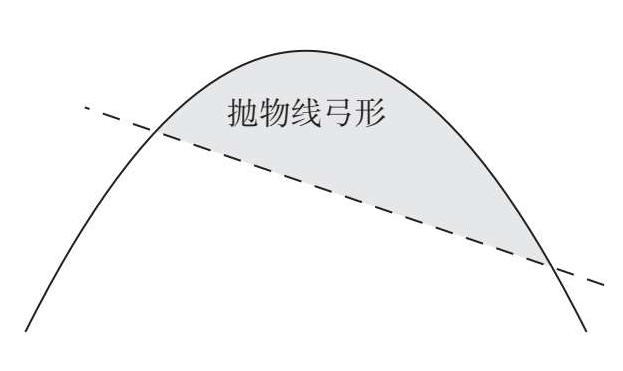
​ 阿基米德采用了一个惊人的方法：迭代（Iterations），他把抛物线弓形想象成了一个由无数三角形碎片粘在一起形成的图形，把这些小三角形的面积加起来，就是抛物线弓形的面积！

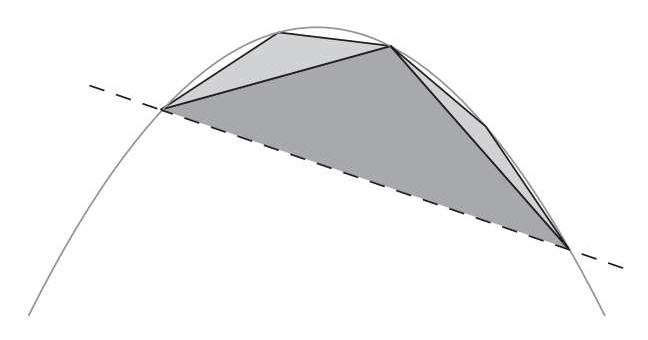
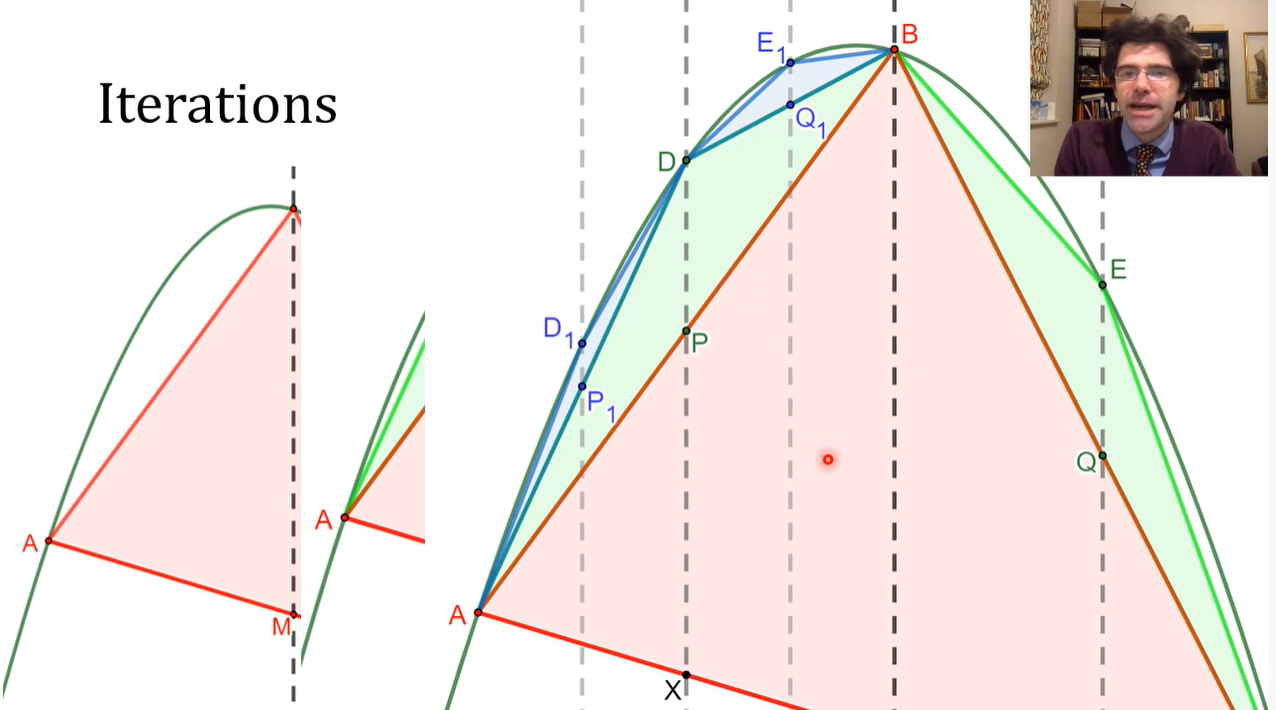
​ 但如何确定每个三角形顶点的位置呢，阿基米德制定了一个规则，将弓形底部的直线向上平移直到与抛物线相切（tangent），那么这个切点就是三角形的顶点，以此类推后面的小三角形也使用这样的规则。

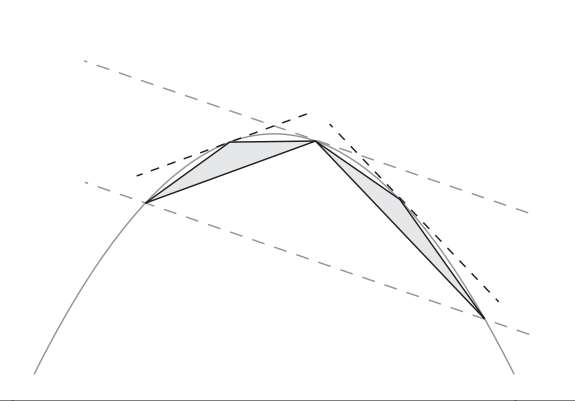
​ 最关键的一点来了，阿基米德证明了每个新构建三角形的面积都是上一层级三角形面积的1/8，因此，如果我们说第一层级的三角形占据了一个面积单位（这个三角形将充当我们的面积标准），那么第二层级的两个三角形一共占据了1/8+1/8=1/4个面积单位。作者并没有给出这部分的证明过程，听说阿基米德在证明它的时候也是用了以前研究抛物线的数学家们的一些成果，他甚至不能自己证明所有的结果。

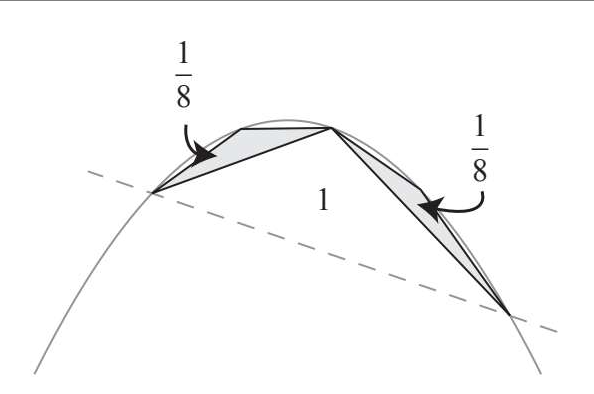
现代数学的证明

​ 既然如此，我们也可以走个捷径，用现代数学的方法来证明它！下证抛物线内每个新构建三角形的面积都是上一层级三角形面积的1/8：

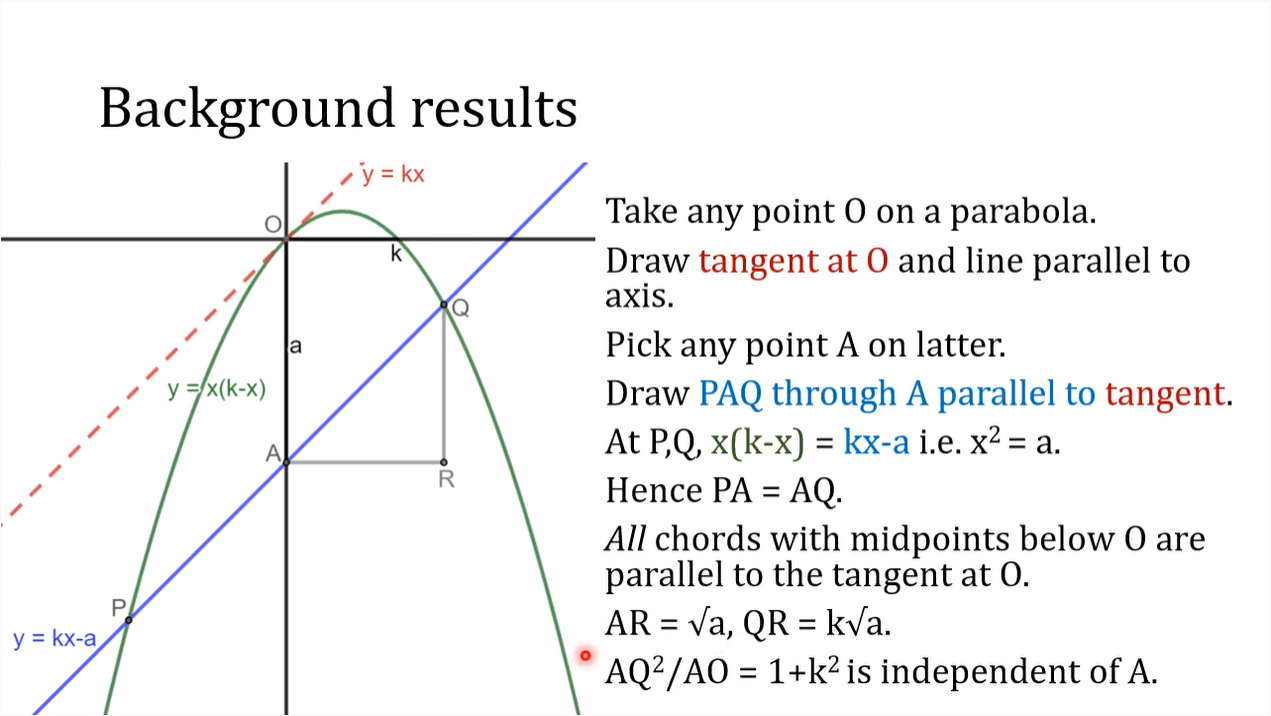
\(在抛物线上取一点 O，建立笛卡尔坐标系，其中 y 轴要平行于抛物线的对称轴\)​​

\(设O点处的切线方程为 y = kx ①，抛物线方程为 y = x(k - x)②\)

\(将切线向下平移长度 a，交抛物线于 P ， Q 两点，交 y 轴于 A 点，则直线 PQ 的方程为 y = kx - a③\)

\(由②③得 x^2 = a ，故 PA = AQ\)​

\(又因为AR = \sqrt{a} ，QR = k\sqrt{a}\)

\(所以\frac {AQ^2}{AO} = 1 + k^2，取决于斜率（gradient）k 的值，与截距 a 无关\)​​​​

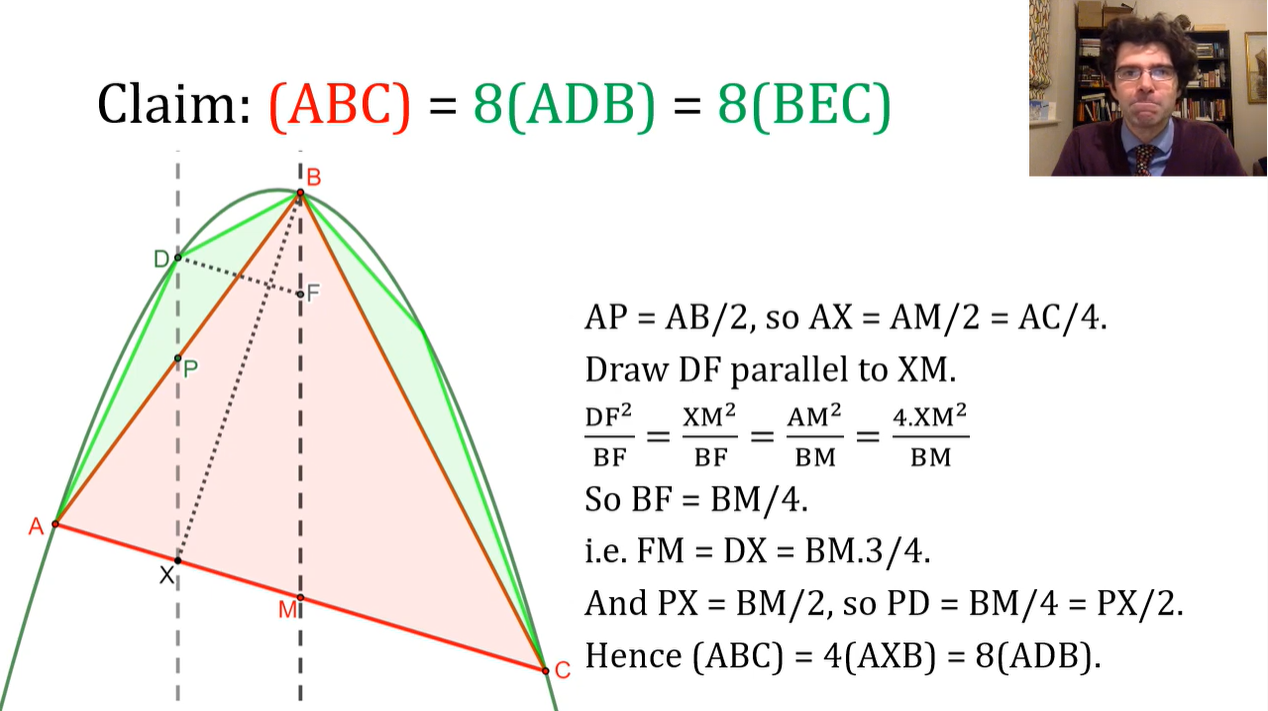
\(由顶点B平行于抛物线对称轴竖直做一条线，交AC于点M，则M为AC的中点\)

\(由顶点D平行于抛物线对称轴竖直做一条直线，交AB于点P，交AC于点X，则P为AB的中点，X为AM的中点\)​

\(故AP = \frac {AB}2，AX = \frac {AM}2 = \frac {AC}4，∆APX ∾ ∆ABM\)​​​

\(做DF平行于XM，则四边形DFMX为平行四边形（parallelogram），DF平行且等于XM\)​​​​

\(所以\frac {DF^2}{BF} = \frac {XM^2}{BF}\)

\(因为\frac {DF^2}{BF} = \frac {AM^2}{BM} = 1 + k^2\)

\(所以\frac {DF^2}{BF} = \frac {XM^2}{BF} = \frac {AM^2}{BM} = \frac {4XM^2}{BM}\)​

\(故BM = 4BF, FM = DX = \frac 34BM\)​

\(因为DX = FM = 3BF，PX = \frac 12BM = 2BF\)​​

\(所以3BF = PD + 2BF，PD = BF = \frac 14BM = \frac 12PX\)​

\(故S∆ADB = \frac 12S∆ABX = \frac 18S∆ABC\)

同理可证其他三角形，证毕。

剩下的工作就是将所有三角形的面积加起来，这其实就是积分学的雏形。假设初始三角形的面积为1，那么其生成的两个小三角形的面积和为其\(\frac 14\)，往后是\(\frac1{16}，\frac 1{64}\)​，依此类推，设抛物线弓形的面积为S，那么有：

\(S = 1 + \frac14 + \frac 1{16} + \frac 1{64} + ···\)

这类无穷级数有个捷径可走，将两边乘4得：

\(4S = 4 + S，故S = \frac 43\)​

面积S是一个永远也无法算完的数，但神奇的是我们可以用一个分数\(\frac 43\)​将其表示出来。就好比圆周率\(Π\)​一样，它是永远也算不完的，但它的确存在。​