特殊矩阵:即指非零元素或零元素的分布有一定规律的矩阵,为了节省存储空间, 我们可以对这类矩阵进行压缩存储;即为多个相同的非零元素只分配一个存储空间;对零元素不分配空间
一、稀疏矩阵
稀疏矩阵:设矩阵A中有s个非零元素,若s远远小于矩阵元素的总数,则称A为稀疏矩阵。
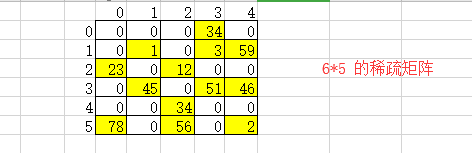
如果我们把整个数据存入内存,如果每个单元格一个字节则需要6*5个字节
我们要对稀疏矩阵进行压缩存储: 即只存储稀疏矩阵中的非零元素和矩阵的大小;采用三元组的表示方式

例如:(6,5,30)矩阵大小、(0,3,34)、(1,1,1)、(1,3,3)、(1,4,59)、(2,0,23)、(2,2,12)、(3,1,45)、(3,3,51)、(3,4,46)、(4,2,34)、(5,0,78)、(5,2,56)、(5,4,2)
稀疏矩阵占用空间大小:7*3个字节
二、三角矩阵:上三角矩阵、下三角矩阵
三角矩阵中的重复元素c(常量)可共享一个存储空间,其余的元素正好有n(n+1)/2个,因此,三角矩阵可压缩存储到向量s[0..n(n+1)/2]中,其中c存放在向量的最后一个分量中
================上三角矩阵=================
以主对角线划分,三角矩阵有上三角和下三角两种。上三角矩阵,它的下三角(不包括主对角线)中的元素均为常数或者0,在大多数情况下,三角矩阵常数为零。

该图就是一个上三角矩阵a(m,n)=a(4,4)是一个4阶的方阵,将该矩阵压缩存储到一维数组S后
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数据 | 1 | 2 | 3 | 4 | 6 | 7 | 8 | 11 | 12 | 16 | 0 |
- 转换后一维数组的长度:S.length=1+n(n+1)/2
- 最后一个位置:S[n(n+1)/2]=0
- 其他上三角元素的位置在一维数组S的下标:S[i(2n-i+1)/2+j-i ]=a(i,j) ;例如 a(2,3)=S[2*(2*4-2+1)/2+3-2]=S[8]=12
================下三角矩阵=================
以主对角线划分,三角矩阵有上三角和下三角两种。下三角矩阵,它的上三角(不包括主对角线)中的元素均为常数或者0,在大多数情况下,三角矩阵常数为零。

该图就是一个上三角矩阵a(m,n)=a(4,4)是一个4阶的方阵,将该矩阵压缩存储到一维数组S后
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 数据 | 1 | 5 | 6 | 9 | 10 | 11 | 13 | 14 | 15 | 16 | 0 |
- 转换后一维数组的长度:S.length=1+n(n+1)/2
- 最后一个位置:S[n(n+1)/2]=0
- 其他下三角元素的位置在一维数组S的下标:S[i(i+1)/2+j]=a(i,j) ;例如 a(2,2)=S[2*(2+1)/2+2]=S[5]=11
三、对称矩阵:
结论:对称矩阵的压缩存储就是使用长度 array[n(n+1)/2-1] 的 一维数组存储对称矩阵
1、下三角
在一个n阶方阵A中,若元素满足下述性质:a(i,j) =a(j,i) 0≤i,j≤n-1 ,则称A为对称矩阵
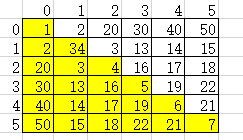
只要存储矩阵中上三角或者下三角中的元素,让每个对称的元素共享一个存储空间,这样能节省近一半的存储空间
转换后一维数组的长度:S.length=n(n+1)/2
最后一个位置:S[n(n+1)/2-1]
其他下三角元素的位置在一维数组S的下标:S[i(i+1)/2+j]=a(i,j) ;例如 a(2,2)=S[2*(2+1)/2+2]=S[5]=4
2、上三角

其他上三角元素的位置在一维数组S的下标:S[i(2n-i+1)/2+j-i]=a(i,j) ;例如 a(2,2)=S[2*(2*6-2+1)/2+2-2]=S[11]=4



