一、图的概念
图的定义
1、图 在树形结构中,结点间具有层次关系,每一层结点只能和上一层中的至多一个结点相关, 但可能和下一层的多个结点相关。而在图结构中,任意两个结点之间都可能相关,即结点之 间的邻接关系可以是任意的
图G:是由集合V和E组成,记成G=(V,E); V 是顶点集(非空);E 是边集 (可空);边是顶点的有序对或无序对;(边反映了两顶点之间的关系)
2、有向图 :边是顶点的有序对的图(图中每条边都用箭头指明了方向)一个具有 n 个顶点的有向完全图的弧 数为 n(n-1)
3、无向图 :边是顶点的无序对的图。一个具有 n 个顶点的无向完全图的边 数为 n(n-1)/2。
4、权、带权图: 图的边附带数值,这个数值叫权。权在实际应用中可表示从一个顶点到另一个顶点的 距离、代价或耗费等。每条边都带权的图称为带权图。
5、顶点的度、入度、出度
- 无向图中顶点 v 的度是与该顶点相关联的边的数目,记为 D(v)。
- 如果 G 是一个有向图,则把以顶点 v 为终点的弧的数目称为 v 的入度,记为 ID(v); 把以顶点 v 为始点的弧的数目称为 v 的出度,记为 OD(v)。 有向图中顶点 v 的度等于入度与出度的和,即 D(v)=ID(v)+OD(v)。
6、子图:设 G=(V,E)是一个图,若 E'是 E 的子集,V'是 V 的子集,并且 E'中的边仅与 V'中的 顶点相关联,则图 G'=(V',E')称为图 G 的子图。
7、路径、路径长度 :在无向图 G= (V,E)中,从顶点 v 到顶点 v'的路径是一个顶点序列:v,vi1,vi2,…, vim, v',其中(v, vi1),(vi1,vi2),…,(vim,v')为图 G 中的边。 若 G 是有向图,则要求这个顶点序列满足:<v,vi1>, <vi1,vi2>,…,<vim,v'>为图 G 中的弧。 路径上边(或弧)的数目称为路径长度。
9、简单路径:除第一个和最后一个外,其余各顶点均不相同的 路径 。
10、 回路 :第一个和最后一个顶点相同的路径,也称环;
11、 简单回路: 第一个和最后一个顶点相同的简单路径;注:回路中可以有多个圈,而简单回路只能有一个圈。
生成树:含有该连通图的全部顶点的一个极小连通子图。若连通图G的顶点个数为n,则G的生成树的边数为n-1。
G的子图G’边数大于n-1,则G’中一定有环。
G的子图G’边数小于n-1,则G’中一定不连通。
生成森林——在非连通图中,每个连通分量都可得到一个极小连通子图,也就是生成树。这些生成树就组成了一个非连通图的生成森林。
图的运算:
➢建立图 GreateGraph(G,V,E)
➢取顶点信息 GetVex(G,u)
➢取边信息 Getarc(G,u,v)
➢查询第一个邻接点FirstVex(G,u)
➢查询下一个邻接点NextVex(G,u,v)
➢插入顶点 InsertVex(G,v)
➢删除顶点 DeleteVex(G,v)
➢插入边 InsertArc(G,v,w)
➢删除边 DeleteArc(G,v,w)
➢遍历图 Travers(G,tag)
二、图的存储结构
1、图的邻接矩阵: 表示图的各顶点之间关系的矩阵,邻接矩阵就是用矩阵来描述图中顶点之间的关联关系,在程序设计语言中很容易用二维 数组来实现矩阵
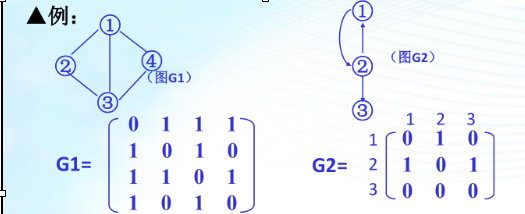
无向图:无向图的邻接矩阵是一个对称矩阵;顶点 vi的度是邻接矩阵中第 i 行(或第 i 列)的元素之和;在含n个顶点和e条边的无向图的邻接矩阵中,零元素的个数为 n^2-2e
有向图:顶点 vi的出度 OD (vi)是邻接矩阵中第 i 行元素之和,顶点 vi的入度 ID (vi) 是邻接矩阵中第 i 列元素之和
2、带权图( 网) 的邻接矩阵

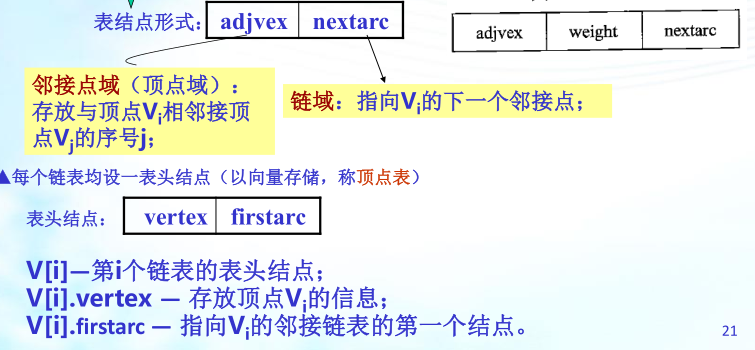
3、邻接表:邻接表是顺序存储与链式存储相结合的存储方法。
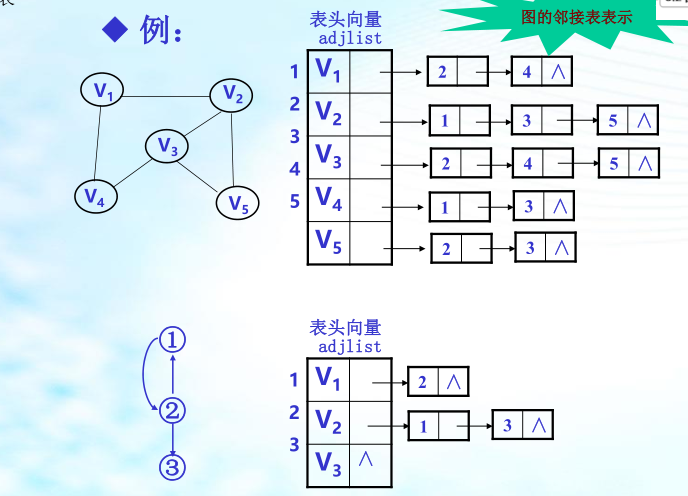
结论:
1)n个顶点、e条边的无向图,则其邻接表的表头结点数为n,链表结点总数为2e;
2)对于无向图,第i个链表的结点数为顶点V i 的度;对于有向图,第i个链表的结点数为顶点V i 的出度;
3)在边稀疏时,邻接表比邻接矩阵省单元;
4)邻接表表示在检测边数方面比邻接矩阵表示效率要高。
三、图的遍历
图的遍历 :从图G 中某一顶点v 出发,顺序访问各顶点一次
为克服顶点的重复访问,设立辅助数组visited[n]。visited[i]=1 顶点i已被访问过;visited[i]=0 顶点i未被访问过
遍历方法:
- 深度优先搜索法DFS (类似先序遍历)
- 广度优先搜索法BFS(类似层次遍历)
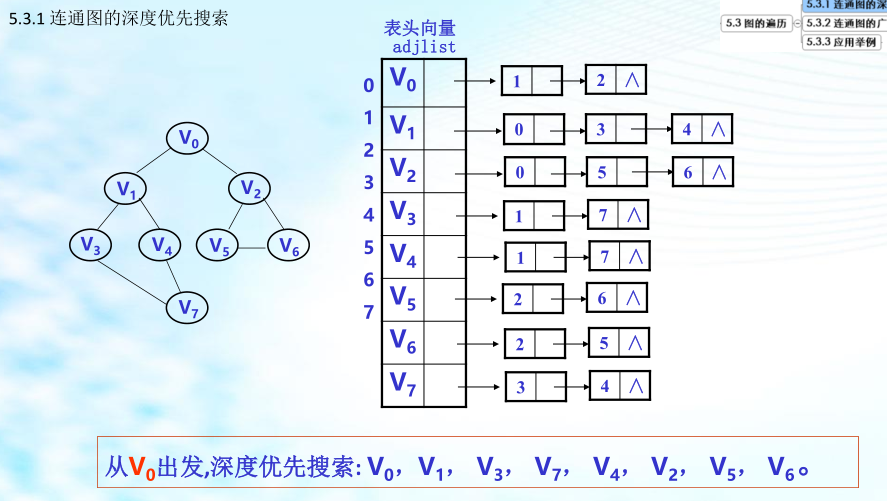
1、连通图的深度优先搜索(DFS)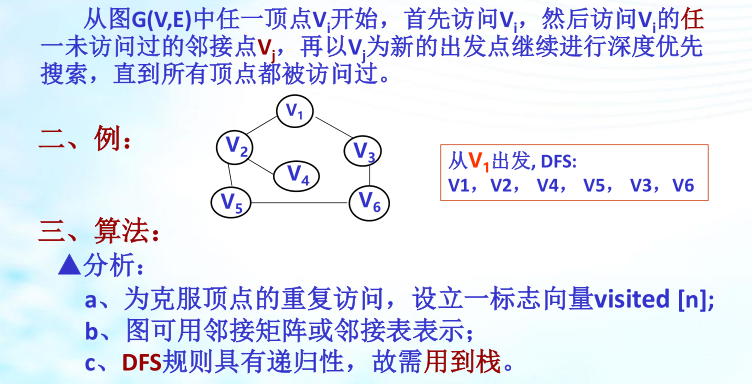
深度优先搜索法算法:对图按深度优先遍历的递归算法( 邻接表 ) 时间复杂度:O(n+e)
深度优先搜索法算法:对图按深度优先遍历的递归算法 ( 邻接矩阵 )时间复杂 度 :O(n*n )
2、连通图的广度优先搜索法(BFS)

判断图的连通性:对图G 调用一次DFS 或BFS ,得到一顶点集合,然后将之与V(G) 比较,若两集合相等,则图G 是连通图,否则就说明有未访问过的顶点,因此图不连通
求图的连通分量:从无向图的每个连通分量的一个顶点出发遍历,则可求得无向图的所有连通分量。
3、最小生成树 :一个图的最小生成树是图所有生成树中权总和最小的生成树。
构造最小生成树的 Prim(普里姆) 算法:适合于求边稠密的带权图的最小生成树
构造最小生成树的克鲁斯卡尔(Kruskal)算法:适合于求边稀疏的网的最小生成树
单源最短路径 给定一个带权有向图 G=(V,E),其中每条边的权是非负实数。另外,给定 V 中的一个 顶点, 称为源。要计算从源到其他各顶点的最短路径长度。这里的长度是指路径上各边权 值之和。这个问题通常称为单源最短路径问题。 Dijkstm(迪杰斯特拉) 算法求单源最短路径问题
四、拓扑排序
AOV 网:如果以图中的顶点来表示活动,有向边表示活动之间的优先关系,这种用顶点表示活动的有向图称为 AOV 网。AOV 网中的弧表示活动之间存在着的制约关系
完成拓扑排序的前提条件是 AOV 网中不允许出现回路。
拓扑排序算法的时间复杂度为 O(n+e)
有向图拓扑排序算法的基本步骤:
- (1) 图中选择一个入度为 0 的顶点,输出该顶点;
- (2) 从图中删除该顶点及其相关联的弧,调整被删弧的弧头结点的入度(入度减 1);
- (3) 重复执行(1)、(2)直到所有入度为 0 的顶点均被输出,拓扑排序完成,或者图中 再也没有入度为 0 的顶点。
可以证明,任何一个无环有向图,其全部顶点可以排成一个拓扑序列。




