数据结构导论之第三章(栈、队列、数组)

栈和队列可看作是特殊的线性表，它们是运算受限的线性表

一、栈

栈：栈是只能在表的一端（表尾）进行 插入和删除的线性表；允许插入及删除的一端（表尾）称为栈顶(Top)； . 另一端（表头）称为栈底(Bottom)；当表中没有元素时称为空栈

进栈：在栈顶插入一元素； 

出栈：在栈顶删除一元素；

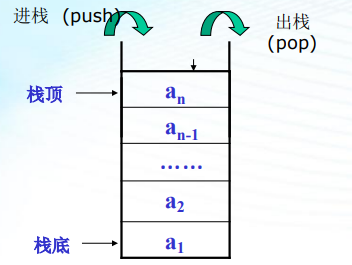
栈的特点：后进先出，栈中元素按a1，a2，a3，…an的次序进栈，出栈的第一个元素应 为栈顶元素。换句话说，栈的修改是按后进先出的原则进行的。 因此，栈称为后进先出线性表（LIFO）。

栈的用途：常用于暂时保存有待处理的数据

1、栈的顺序实现：顺序栈

• ● 栈容量——栈中可存放的最大元素个数；
• ● 栈顶指针 top——指示当前栈顶元素在栈中的位置；
• ● 栈空——栈中无元素时，表示栈空；
• ● 栈满——数组空间已被占满时，称栈满；
• ● 下溢——当栈空时，再要求作出栈运算，则称“下溢”；
• ● 上溢——当栈满时，再要求作进栈运算，则称“上溢”。

 

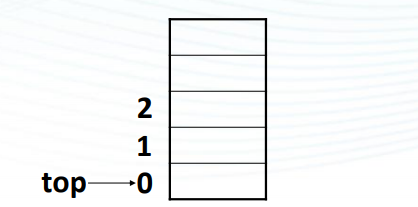
 约定栈的第1个元素存在data[1]中, 则： s->top==0 代表顺序栈s为空； s->top==maxsize-1 代表顺序栈s为满 ；

//栈大小
const int maxsize=6;
//1、顺序栈类型的定义
typedef struct seqstack {
    DataType data[maxsize];
    int top;
}SeqStk;

//2、栈的初始化
int Initstack(SeqStk *stk){
    stk->top=0;
    return 1;
}
//3、判断空栈（栈空时返回值为1，否则返回值为0）
int EmptyStack(SeqStk *stk){
    if(stk->top= =0){
        return 1;
    }else{
        else return 0;
    } 
}
/*4、进栈 数据元素x进顺序栈sq*/
int Push(SeqStk *stk, DataType x){
     /*判是否上溢*/
    if（stk->top==maxsize -1){ 
        error(“栈满”);return 0;
    } else {
        stk->top++；/*修改栈顶指针，指向新栈顶*/
        stk->data[stk->top]=x; /*元素x插入新栈顶中*/
        return 1;
    }
}
/*5、出栈 顺序栈sq的栈顶元素退栈*/
int Pop(SeqStk *stk){
     /*判是否下溢*/
    if（stk->top==0）{
         error(“栈空”);
         return 0;
     }else {
        stk->top-- ； /*修改栈顶指针，指向新栈顶*/
        return 1;
    }
}
//6、 取栈顶元素
DataType GetTop(SeqStk *stk){
    if(EmptyStack(stk)){
        return NULLData;
    }else{
        return stk->data[stk->top];
    }
}

双栈
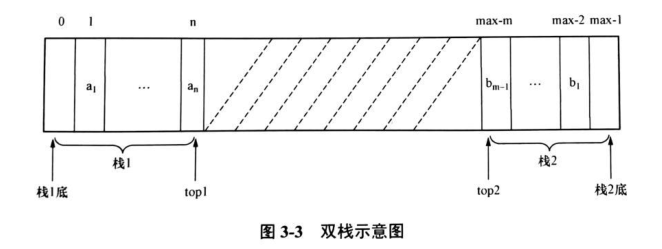
在某些应用中，为了节省空间，让两个数据元素类型一致的栈共享一维数组空间 data[max]，成为双栈，两个栈的栈底分别设在数组两端，让两个栈彼此迎面“增长”，两个栈的栈顶变量分别为 top1、top2，仅当两个栈的栈顶位置在中间相遇时（top1 + 1 =top2）才发生“上溢”，判栈空时，两个栈不同，当 top1=0 时栈 1 为空栈，top2=max-1 时栈 2 为空桟。双栈如图：

2、栈的链接实现：链栈

栈的链式存储结构称为链栈，它是运算受限的单链表， 插入和删除操作仅限制在表头位置上进行。栈顶指针就是链 表的头指针

 

 下溢条件：LS->next==NULL；上溢：链栈不考虑栈满现象

//1、链栈的定义
typedef struct node{
    DataType data;
    struct node *next
} LkStk;
//2、链栈的初始化
void InitStack(LkStk *LS){
    LS=(LkStk *)malloc(sizeof(LkStk));
    LS->next=NULL;
}
//3、判断栈空
int EmptyStack(LkStk *LS){
    if(LS->next= =NULL){
        return 1;
    } else{
        return 0;
    } 
}
//4、进栈:在栈顶插入一元素x:生成新结点（链栈不会有上溢情况发生）;将新结点插入链栈中并使之成为新的栈顶结点
void Push (LkStk *LS, DataType x){ 
    LkStk *temp;
    temp= (LkStk *) malloc (sizeof (LkStk));
    temp->data=x;
    temp->next=LS->next;
    LS->next=temp;
}
//5、出栈:在栈顶删除一元素，并返回;考虑下溢问题;不下溢，则取出栈顶元素，从链栈中删除栈顶结点并将结点回归系统
int Pop (LkStk *LS){ 
    LkStk *temp;
    if (!EmptyStack (LS)){ 
        temp=LS->next;
        LS->next=temp->next;
        free(temp);
        return 1;
    }else{
        return 0;
    }
}
//6、取栈顶元素
DataType GetTop(LkStk *LS){
    if (!EmptyStack(LS)){
        return LS->next->data;
    }else{
        return NULLData;
    }
}

 二、队列

队列(Queue)也是一种运算受限的线性表。

队列：是只允许在表的一端进行插入，而在另一 端进行删除的线性表。

其中：允许删除的一端称为队头(front)， 允许插入的另一端称为队尾(rear)。 队列 Q=(a1，a2，a3，…an )

 

 队列特点：先进先出（FIFO）；常用于暂时保存有待处理的数据

1、队列的顺序实现

队列的顺序实现：一般用一维数组作为队列的存储结构

队列容量：队列中可存放的最大元素个数

初始： front=rear=0

进队： rear增1，元素插入尾指针所指位置

出队： front增1，取头指针所指位置元素

队头指针front：始终指向实际队头元素的前一位置

队尾指针 rear：始终指向实际队尾元素

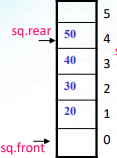
//顺序队列的构造
const int maxsize=20;
typedef struct seqqueue {
    DataType data[maxsize];
    int front, rear ;
}SeqQue;
SeqQue sq;

入队列操作：sq.rear=sq.rear+1;sq.data[sq.rear]=x;
出队列操作：sq.front=sq.front+1;
上溢条件：sq.rear = = maxsize-1 ( 队满 )
下溢条件：sq.rear = = sq.front (队列空)
顺序队列的假溢出：sq.rear == maxsize-1，但队列中实际容量并未达到最大容量的现象;极端现象:队列中的项不多于1,也导致“上溢”.假溢出浪费空间循环队列可以解决该问题

2、循环队列

为队列分配一块存储空间(数组表示)，并将 这一块存储空间看成头尾相连接的。

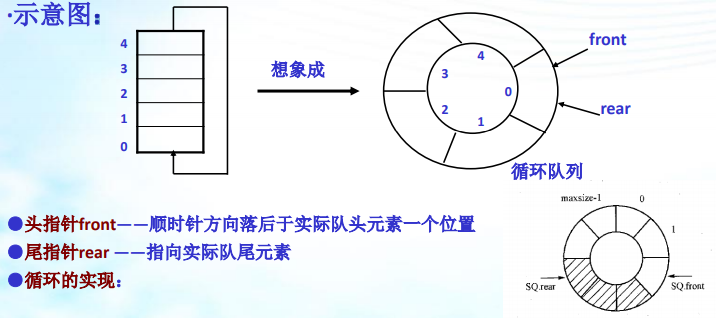
对插入即入队： 队尾指针增1,Sq.rear=(sq.rear+1)%maxsize
对删除即出队： 队头指针增1,Sq.front=(sq.front+1)%maxsize
下溢条件即队列空：CQ.front==CQ.rear
上溢条件即队列满：尾指针从后面追上头指针，(CQ.rear+1)%maxsize==CQ.front（浪费一个空间，队满时实际队容量=maxsize-1）

设以数组Q[m]存放循环队列的元素，变量rear和queuelen分别表示循环队列中队尾元素的下标位置和元素的个数。则计算该队列中队头元素下标位置的公式是 (rear-queuelen+m)%m

例题：

(rear-front+n)%n=(7-8+100)%100=99

例题：

 

 

//循环队列的定义
typedef struct Cycqueue{
    DataType data[maxsize];
    int front,reat;
}CycQue;
CycQue CQ;

//循环队列的初始化
void InitQueue(CycQue CQ){
    CQ.front=0;
    CQ.rear=0;
}
//循环队列判断空
int EmptyQueue(CycQue CQ){
    if (CQ.rear==CQ.front){
        return 1;
    } else{
        else return 0;
    }
}
入队——在队尾插入一新元素x
● 判上溢否？是，则上溢返回；
● 否则修改队尾指针（增1），新元素x插入队尾。
int EnQueue(CycQue CQ,DataType x){
    if ((CQ.rear+1)%maxsize==CQ.front){
        error(“队列满”);return 0;
    }else {
        CQ.rear=(CQ.rear+1)%maxsize;
        CQ.data[CQ.rear]=x;
        return 1;
    }
}
出队——删除队头元素，并返回
● 判下溢否？是，则下溢返回；
● 不下溢，则修改队头指针，取队头元素。
int OutQueue(CycQue CQ){
    if (EmptyQueue(CQ)){
        error(“队列空”);
        return 0;
    }else {
        CQ.front=(CQ.front+1)%maxsize;
        return 1；
    }
}
//.取队列首元素
DataType GetHead(CycQue CQ){
    if (EmptyQueue(CQ)){
        return NULL;
    }else{
        return CQ.data[(CQ.front+1)%maxsize];
    }
}

 3、队列的链接实现

队列的链接实现实际上是使用一个带有头结点的单链表来表示队列，称为链队列。头指针指向链表的头结点，单链表的头结点的next 域指向队列首结点，尾指针指向队列尾结点，即单链表的最后一个结点；队列的链式实现是动态申请空间，所以不会存在队满的情况。

 

 

 

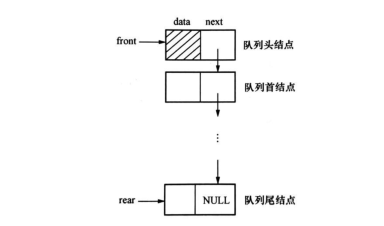
//类型定义
typedef struct LinkQueueNode{
    DataType data;
    struct LinkQueueNode *next;
} LkQueNode;
typedef struct LkQueue{
    LkQueNode *front, *rear;
}LkQue;
LkQue LQ;
由于链接实现需要动态申请空间，故链队列在一定范围内不会出现队列满的情况，当（LQ.front==LQ.rear）成立时，队列中无数据元素，此时队列为空
//（1）队列的初始化
void InitQueue(LkQue *LQ){
    LkQueNode *temp;
    temp= (LkQueNode *)malloc (sizeof (LkQueNode)); //生成队列的头结点
    LQ->front=temp; //队列头才旨针指向队列头结点
    LQ->rear=temp; //队列尾指针指向队列尾结点
    (LQ->front) ->next=NULL;
}
//判队列空
int EmptyQueue(LkQue LQ){
    if (LQ.rear==LQ.front){
        return 1; //队列为空
    }else{
        return 0;
    }
}
//入队列
void EnQueue(LkQue *LQ;DataType x){
    LkQueNode *temp;
    temp=(LkQueNode *)malloc(sizeof(LkQueNode));
    temp->data=x;
    temp->next=NULL;
    (LQ->rear)->next=temp; //新结点入队列
    LQ->rear=temp; //置新的队列尾结点
}
//出队列
OutQueue(LkQue *LQ){
    LkQueNode *temp;
    if (EmptyQueue(CQ)){ //判队列是否为空
        error(“队空”); //队列为空
        return 0;
    }else { //队列非空
        temp=(LQ->front) ->next; //使 temp 指向队列的首结点
        (LQ->front) ->next=temp->next; //修改头结点的指针域指向新的首结点
        if (temp->next==NULL){
            LQ->rear=LQ->front; //无首结点时，front 和 rear 都指向头结点
        }
        free(temp);
        return 1;
    }
}
//取队列首元素
DataType GetHead (LkQue LQ){
    LkQueNode *temp;
    if (EmptyQueue(CQ)){
        return NULLData; //判队列为空，返回空数据标志
    }
    else {
        temp=LQ.front->next;
        return temp->data; //队列非空，返回队列首结点元素
    }
}

三、数组

数组：是线性表的推广，其每个元素由一个值和一组下标组成，其中下标个数称为数组的维数

一维数组：数组可以看成线性表的一种推广，一维数组又称向量，它由一组具有相同类型的数据元素组成，并存储在一组连续的存储单元中

多维数组：若一维数组中的数据元素又是一维数组结构，则称为二维数组；依此类推，若一维数组中的元素又是一个二维数组结构，则称作三维数组,一般地，一个 n 维数组可以看成元素为 （n-1） 维数组的线性表，多维数组是线性表的推广

二维数组Amn可以看成是由m个行向量组成的向量，也可以看成是n个列向量组成的向量。

数组一旦被定义，它的维数和维界就不再改变。因此，除了结构的初始化和销毁之外，数组通常只有两种基本运算：

• 读：给定一组下标，返回该位置的元素内容；
• 写：给定一组下标，修改该位置的元素内容。

数组的存储结构
一维数组元素的内存单元地址是连续的，二维数组可有两种存储方法：一种是以列序为主序的存储；另一种是以行序为主序的存储。数组元素的存储位置是下标的线性函数

1. 存储结构：顺序存储结构
　　由于计算机的内存结构是一维的，因此用一维内存来表示多维数组，就必须按某种次序将数组元素排成一列序列，然后将这个线性序列存放在存储器中;又由于对数组一般不做插入和删除操作，也就是说，数组一旦建立，结构中的元素个数和元素间的关系就不再发生变化。因此，一般都是采用顺序存储的方法来表示数组。

 

 

 2、矩阵的压缩存储

为了节省存储空间， 我们可以对这类矩阵进行压缩存储：即为多个相同的非零元素只分配一个存储空间；对零元素不分配空间。

特殊矩阵：即指非零元素或零元素的分布有一定规律的矩阵。下面我们讨论几种特殊矩阵的压缩存储。

 

 

 

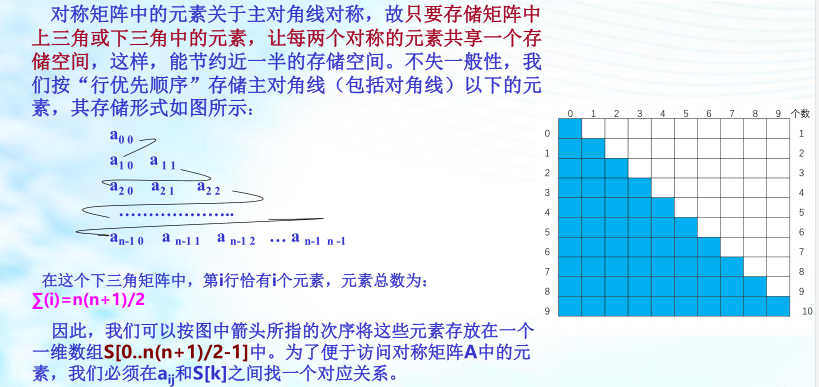
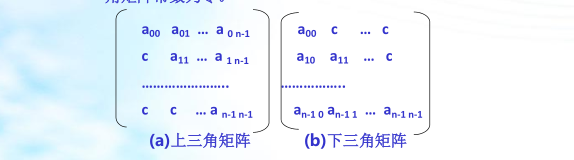
三角矩阵
以主对角线划分，三角矩阵有上三角和下三角两种。上三角矩阵如图所示，它的下三角（不包括主对角线）中的元素均为常数。下三角矩阵正好相反，它的主对角线上方均为常数，如图所示。在大多数情况下，三角矩阵常数为零。

 

 三角矩阵中的重复元素c可共享一个存储空间，其余的元素正好有n(n+1)/2个，因此，三角矩阵可压缩存储到向量s[0..n(n+1)/2]中，其中c存放在向量的最后一个分量中。

稀疏矩阵

什么是稀疏矩阵:简单说，设矩阵A中有s个非零元素，若s远远小于矩阵元素的总数，则称A为稀疏矩阵。
稀疏矩阵的压缩存储： 即只存储稀疏矩阵中的非零元素。由于非零元素的分布一般是没有规律的，因此在存储非零元素的同时，还必须同时记下它所在的行和列的位置（i,j)。
反之，一个三元组(i,j,aij )唯一确定了矩阵A的一个非零元。因此，稀疏矩阵可由表示非零元的三元组及其行列数唯一确定。

 

 稀疏矩阵的三元组顺序表表示法——将矩阵中的非零元素化成三元组形式并按行的递减次序（同行按列的递增次序）存放在内存中。