
一、线性表的基本概念
线性表是由n(n≥0)个数据元素(结点)a1,a2,a3,……an组成的有限序列;数据元素的个数n定义为表的长度。当n=0时,称为空表。
将非空的线性表(n>0)记作:L=(a1,a2,a3,……,an)
- a1:起始结点(没有直接前驱)
- an:终端结点(没有直接后继)。
- a1称为a2的直接前驱
- a3称为a2的直接后继
线性表的特点:
- 线性表中只有1个起始结点,1个终端结点,
- 起始结点没有直接前驱,有1个直接后继。
- 终端结点有1个直接前驱,没有直接后继。
- 除这2个结点外,每个结点都有且只有1个直接前驱和1个直接后继。
线性表的基本运算
- 1,初始化 Initiate(L) :建立一个空表L=(),L不含数据元素。
- 2,求表长度 Length(L):返回线性表L的长度。
- 3,取表元 Get(L,i):返回线性表第i个数据元素,当i不满足1≤i≤Length(L)时,返回一特殊值。
- 4,定位 Locate(L,x):查找线性表中数据元素值等于x的结点序号,若有多个数据元素值与x相等,运算结果为这些结点中序号的最小值,若找不到该结点,则运算结果为0。
- 5,插入 Insert(L,x,i):在线性表L的第i个数据元素之前插入一个值为x的新数据元素,参数i的合法取值范围是1≤i≤n+1。操作结束后线性表L由(a1,a2,…,ai-1,ai,ai+1,.…,an )变为(a1,a2,…,ai-1,x,ai,ai+1 .…,an )表长度加1。
- 6,删除 Delete(L,i):删除线性表L的第i个数据元素ai ,i的有效取值范围是1≤i≤n。删除后线性表L由(a1,a2,…,ai-1,ai,ai+1,.…,an )变为(a1,a2,…,ai-1,ai+1,.…,an ),表长度减1
二、线性表的顺序存储
线性表顺序存储的方法:将表中的结点依次存放在计算机内存中一组连续的存储单元中。
- ◆ 数据元素在线性表中的邻接关系决定其在存储空间中的存储位置。
- ◆ 即逻辑结构中相邻的结点,其物理存储位置也相邻。
- ◆ 用顺序存储实现的线性表称为顺序表。一般使用数组存储
顺序存储结构的特点:
- 线性表的逻辑结构与存储结构一致
- 可以对数据元素实现随机读取
- 设线性表中所有结点的类型相同,则每个结点所占用存储空间大小亦相同。
- 假设表中每个结点占用L个存储单元,其中第一个单元的存储地址则是该结点的存储地址
- 并设表中开始结点a1 的存储地址是d,那么结点ai 的存储地址LOC(ai)=d+(i-1)*L
顺序表是用一维数组实现的线性表,数组下标可以看成是元素的相对地址;逻辑上相邻的元素,存储在物理位置也相邻的单元中
1、线性表的基本运算在顺序表上的实现
=======================插入========================
插入 Insert(L,x,i):在线性表L的第i个数据元素之前插入一个值为x的新数据元素,参数i的合法取值范围是1≤i≤n+1。操作结束后线性表L由(a1,a2,…,ai-1,ai,ai+1,.…,an )变为(a1,a2,…,ai-1,x,ai,ai+1 .…,an )表长度加1。
注意:
- 当表空间已满,不可再做插入操作。
- 当插入位置是非法位置,不可做正常的插入操作。
顺序表插入操作过程
- ① 将表中位置为n ,n-1,…,i上的结点,依次后移到位置n+1,n,…,i+1上,空出位置i。
- ② 在位置i上插入新结点x。(当插入位置i=n+1时,无须移动结点,直接将x插入表的末尾)
- ③ 该顺序表长度加1。
结论:
- 假设线性表中含有n个数据元素,在进行插入操作时,有n+1个位置可插入,在每个位置插入数据的概率是:1/(n+1),在i位置插入时,要移动n-i+1个数据
- 假定在n+1个位置上插入元素的可能性均等,则平均移动元素的个数为:n/2,平均时间复杂度O(n)

===================删除========================
删除 Delete(L,i):删除线性表L的第i个数据元素ai ,i的有效取值范围是1≤i≤n。删除后线性表L由(a1,a2,…,ai-1,ai,ai+1,.…,an )变为(a1,a2,…,ai-1,ai+1,.…,an ),表长度减1
注意:当要删除元素的位置i不在表长范围内(即i<1或i>L->length)时,为非法位置,不能做正常的删除操作
顺序表删除操作过程:
- 1,若i=n,则只要删除终端结点,无须移动结点;
- 2,若1≤i≤n-1,则必须将表中位置i+1,i+2,…,n的结点,依次前移到位置i,i+1,…,n-1上,以填补删除操作造成的空缺。
- 3,该表长度减1
删除算法的分析
- 假设线性表中含有n个数据元素,在进行删除操作时,有n个位置可删除;每个位置删除数据的概率是:1/n,在i位置删除时,要移动n-i个数据;
- 假定在n个位置上删除元素的可能性均等,则平均移动元素的个数为:(n-1)/2;平均时间复杂度O(n)

插入和删除的结论:顺序存储结构表示的线性表,在做插入或删除操作时,平均需要移动大约一半的数据元素。当线性表的数据元素量较大,并且经常要对其做插入或删除操作时,这一点需要值得考虑。

===================定位=================
定位(查找):定位运算LocateSeqlist(L,X)的功能是求L中值等于X的结点序号的最小值,当不存在这种结点时结果为0。
算法的过程:从第一个元素 a1 起依次和x比较,直到找到一个与x相等的数据元素,则返回它在顺序表中的存储下标或序号;或者查遍整个表都没有找到与 x 相等的元素,返回0。
算法分析:
- 最好情况下,第1个元素就是x值,此时查找比较次数为1。
- 最坏情况下,最后1个元素是x值,此时查找比较次数为n。
- 故平均查找长度为(n+1)/2。平均时间复杂度O(n)


三、线性表的链接存储
链式存储的结构:数据项 + 指针项
链表(Link List):使用链式存储的线性表
链表的具体存储表示为:用一组任意的存储单元来存放; 链表中结点的逻辑次序和物理次序不一定相同,还必须存储指示其后继结点的地址信息。

所有结点通过指针链接而组成单链表
NULL称为空指针
Head称为 头指针变量,存放链表中第一个结点地址;在单链表中,增加头结点的目的是方便运算的实现
链表的表示:由于我们常常只注重结点间的逻辑顺序,不关心每个结 点的实际位置,可以用箭头来表示链域中的指针,单链表就 可以表示为下图形式。
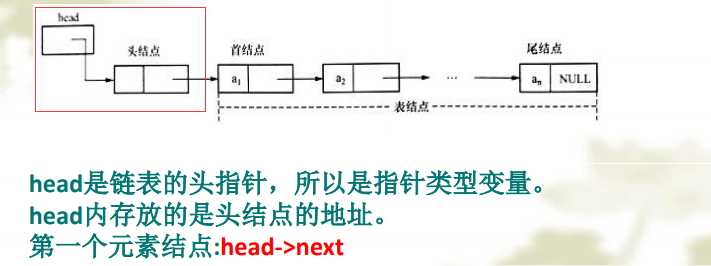
单链表特点:
❖ 起始节点又称为首结点,无前驱,故设头指针head 指向开始结点。
❖ 链表由头指针唯一确定,单链表可以用头指针的名字 来命名。头指针名是head的链表可称为表head。
❖ 终端结点又称尾结点,无后继,故终端结点的指针域 为空,即NULL
❖ 除头结点之外的结点为表结点
❖ 为运算操作方便,头结点中不存数据
单链表的基本运算
=====================初始化=====================
空表由一个头指针和一个头结点组成;在算法中,变量head是链表的头指针,它指向新创建的结点,即头结 点。一个空单链表仅有一个头结点,它的指针域为NULL。

====================求表长====================
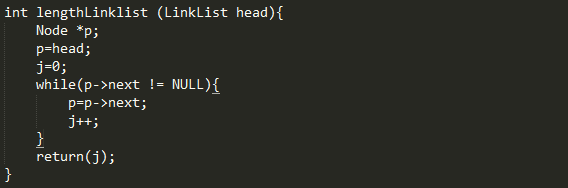
在单链表存储结构中,线性表的长度等于单链表所 含结点的个数(不含头结点)
步骤:
1,令计数器j为0
2,令p指向头结点
3,当下一个结点不空时,j加1,p指向下一个结点
4,j的值即为链表中结点个数,即表长度
=================读表元素:查找第i个结点============
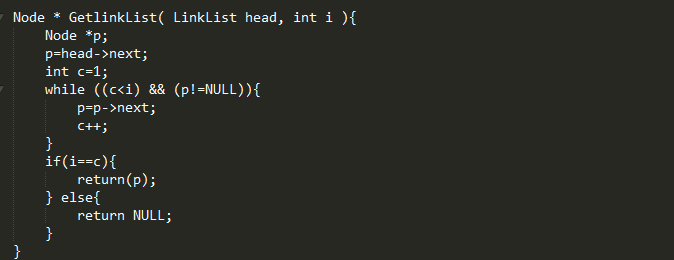
步骤:
1、令计数器j为0
2、令p指向头结点
3、当下一个结点不空时,并且j<i 时,j加1,p指向下一个结点
4、如果j等于i,则p所指结点为要找的第i结点否则,链表中无第i结点
===============定位=================
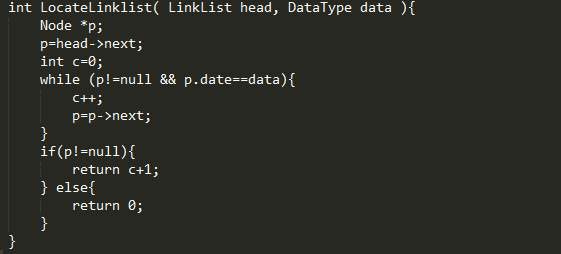
定位运算是对给定表元素的值,找出这个元素的位置。对 于单链表,给定一个结点的值,找出这个结点是单链表的 第几个结点。定位运算又称为按值查找。
具体步骤:
1、令p指向头结点
2、令i=0
3、当下一个结点不空时,p指向下一个结点,同时i的值加1
4、直到p指向的结点的值为x,返回i+1的值。
5、如果找不到结点值为x的话,返回值为0
===================插入====================


===========删除===========
删除运算是将表的第i个结点删去。
(1)找到ai-1的存储位置p
(2)令p->next指向ai的直接后继结点
(3)释放结点ai的空间,将其归还给"存储池" 。
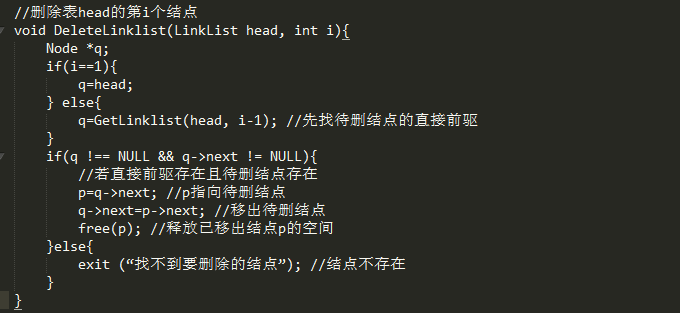
free(p)是必不可少的,因为当一个结点从链表移出后,如果不释放它的空间,它将变成一个无用的结点,它会一直占用着系统内存空间,其他程序将无法使用这块空间。
四、单项循环链表
普通链表的终端结点的next值为NULL;循环链表的终端结点的next指向头结点,在循环链表中,从任一结点出发能够扫描整个链表。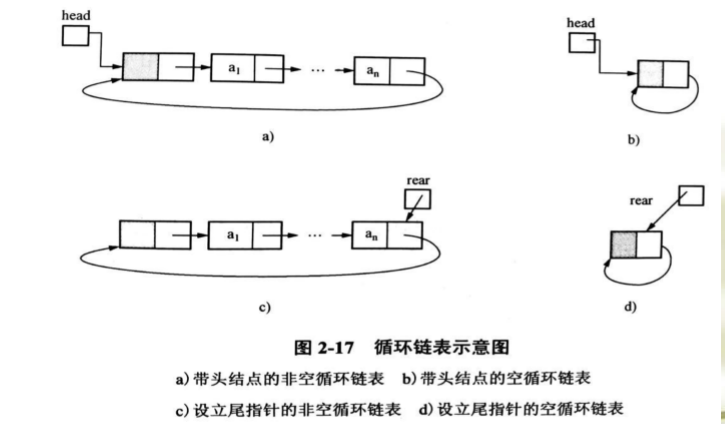
如何找到循环链表的尾结点:在循环链表中附设一个 rear 指针指向尾结点,适用于经常使用头尾结点的链表操作中
若p为指向循环链表中某链结点的指针变量,判断循环链表是否只有一个结点的标志是:p->next=p
五、双向循环链表
在链表中设置两个指针域,一个指向后继结点,一个指向前驱结点这样的链表叫做双向链表
双向循环链表适合应用在需要经常查找结点的前驱和后继的场合。找前驱和后继的复杂度均为:O(1)
双向链表中结点的删除:设p指向待删结点,删除*p可通过下述语句完成:
- (1)p->prior->next=p->next; //p前驱结点的后链指向p的后继结点
- (2)p->next->prior=p->prior; //p后继结点的前链指向p的前驱结点
- (3)free(p); //释放*p的空间;(1)、(2)这两个语句的执行顺序可以颠倒。
双向链表中结点的插入:在p所指结点的后面插入一个新结点*t,需要修改四个指针
- (1)t->prior=p;
- (2)t->next=p->next;
- (3)p->next->prior=t;
- (4)p->next=t;
六、顺序实现与链式实现的比较
线性表与链表的优缺点:
(1)单链表的每个结点包括数据域与指针域,指针域需要占用额外空间。
(2)从整体考虑,顺序表要预分配存储空间,如果预先分配得过大,将造成浪费,若分配得过小,又将发生上溢;单链表不需要预先分配空间,只要内存空间没有耗尽,单链表中的结点个数就没有限制。
(3)、插入、删除操作,顺序表需要移动元素,而链表不需要移动元素
时间性能的比较
顺序表
- 读表元 O(1)
- 定位(找x) O(n)
- 插入O(n)
- 删除O(n)
链表
- 读表元O(n)
- 定位(找x)O(n)
- 插入O(n)
- 删除O(n)



