计算方法（一）——计算机求积分方法，机械求积法
机械求积法
转载请注明出处！
一、引言
随着人工智能的兴起，在计算机领域又一次掀起了数学热，不管是传统的机器学习，还是现在的深度学习，都离不开积分的支撑，那计算机在底层到底是怎样求积分的呢?小编同大家一起探讨。
二、理论推导
我们知道，在我们所学的微积分中我们是通过牛顿-莱布尼兹公式进行求解，然而在实际运用中我们往往会遇到比较复杂的函数，他们的原函数我们往往是找不到的，这个时候我们应该怎么求解呢？
我们不难想的办法是定义法，也就是把区间进行划分，当分点非常多的时候我们就可以用矩形面积代替曲线所围成的面积，然而我们为了得到精度很高的结果往往需要划分等多区间，这样计算的次数将大大增加。
那应该怎么优化呢？这里我们介绍一种求积分的办法：机械求积法。
机械求积分法前戏：
在微积分中我们求定积分时不仅有牛顿-莱布尼兹公式，同时还有积分中值定理：
若函数
在闭区间 
上连续,，则在积分区间上至少存在一个点
，使下式成立
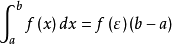
我们从上式子出发，将求积分的问题转化为找某一个的问题，那怎么替代呢？
假设我们的函数是一个0次函数也就是一个F(x) = C 是一个常函数时候，在[a,b]区间的定积分就是(a-b)*f(a),也就是矩形面积，这样我们的f()=f(a)，我们继续加入是一次的呢？F(x) = ax + b
我们很容易想到这个图形是一个梯形。
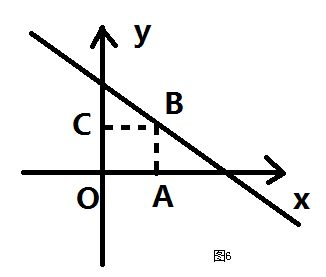
因而其积分=(b-a)*[f(a)+f(b)]/2，这就是我们的梯形公式，这里的f()=[f(a)+f(b)]/2,那问题来了，要是函数是一个不规则的曲线呢？那我们该怎么做呢？
很容易想到的就是把区间细分成很多个小区间，然后在每个区间找一个合适的f(),然后再求积分，再求和就好了，是的这就是们的思路，这个办法就是机械求积法。我们下面给出定义：
机械求积法：
三、代数精度概念
在知道机械求积公式之后，那我们怎么检验一个求积公式的好坏的？这里我们引入代数精度的概念。
定义：
如果某个求积公式对于次数不超过m的多项式均能准确成立，而对于m+1次的的多项式不准确成立，则称该公式具有m次代数精度。
（代数精度越高，越精确）
我们来看看梯形公式的代数精度：(在验证时候只要取1,x,x^2,x^3.......等就行了，其他都可以由这几个组合而成)
F(x) = (b-a)*[f(a)+f(b)]/2,当 f(x) = 1时候，设a=0,b=1,显然成立,而f(x) = x 时，用牛顿-莱布尼兹公式算得：x^2/2|10 = 0.5,而用梯形公式得到的也是0.5，这样对于f(x) = x时也精确成立，而当f(x) = x^2时候则不成了，那么我们就说
梯形公式具有一次代数精度，其他的代数精度的确定方法也同上。
四、插值型求积公式
我们在第二部分时候知道，我们的目的就是不断的划分区间直到有办法精确的求出积分（找到f()),此外呢，我们还可以通过插值法拟合曲线，把问题转化为数值问题。
（没有接触插值法的可以移步） 见鬼吧拉格朗日插值法
这里我们用插值得到的插值多项式子替代原函
这就是插值型积分公式，这样我们就通过插值法可以减少运算，然而这并不是我们最终要的，这只是个开始，更牛的还在后头，请持续关注Jack计算方法系列博客。
转载请注明出处！
点击看看主页其他内容呗！
