多项式计算之秦九韶算法

多项式求值与秦九韶算法

一、引言

　　多项式函数常常用于描述现实世界的各种规律，而在用计算机计算多项式的值的时候，不同算法的计算时空复杂度通常不一样。如一个n次多项式

　　f(x)=a[n]x^n+a[n-1]x^(n-1)+......+a[1]x+a[0],我们的常规计算办法是，直接计算，这样我们的时间复杂度为:O(n^2)

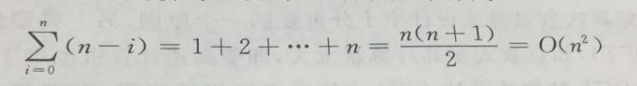
下面我们介绍秦九韶算法：

其核心思想：后面每一次计算都依赖于前面计算的结果，这样以减少重复的计算。

简单引例:

       计算 x^8 直接算将算8次乘法，而这8次都是必要的吗？显然不是，当我们知道x^2的值后，计算x^4只需要用x^2*x^2即可。秦九韶算法正是这样来减少计算量的。

一、推导

　　

 

       

　　

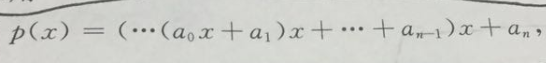
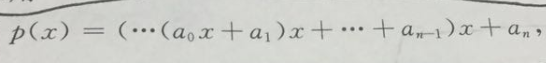
　　a0--->an依次是最高项，到常数项系数

　　从而bn就是所求的解

三、算法描述

       由以上推导知，bn就是我们所求的值，要求bn就得逆推到b0,由于b0=a0我们就可以求出b1依次下去就可以求出bn。

数据结构:

       1.数组

                     1.a[]用于保存系数

                     ps:一般做法还需要保存b[],我们这里只是用到前一项，所以一个常数即可

 

c++实现：

 

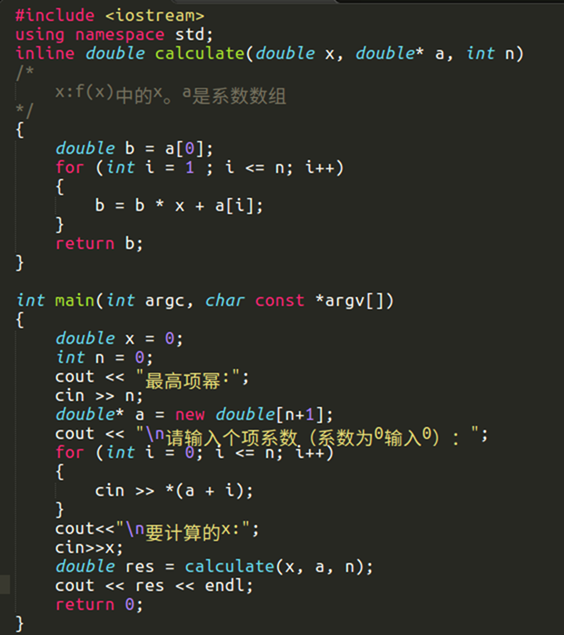
#include <iostream>
using namespace std;
inline double calculate(double x, double* a, int n)
/*
    x:f(x)中的x。a是系数数组
*/
{
    double b = a[0];
    for (int i = 1 ; i <= n; i++)
    {
        b = b * x + a[i];
    }
    return b;
}

int main(int argc, char const *argv[])
{
    double x = 0;
    int n = 0;
    cout << "最高项幂:";
    cin >> n;
    double* a = new double[n+1];
    cout << "\n请输入个项系数（系数为0输入0）：";
    for (int i = 0; i <= n; i++)
    {
        cin >> *(a + i);
    }
    cout<<"\n要计算的x:";
    cin>>x;
    double res = calculate(x, a, n);
    cout << res << endl;
    return 0;
}