什么是哈夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
基本术语
哈夫曼树又称最优树
1️⃣ 路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。
通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
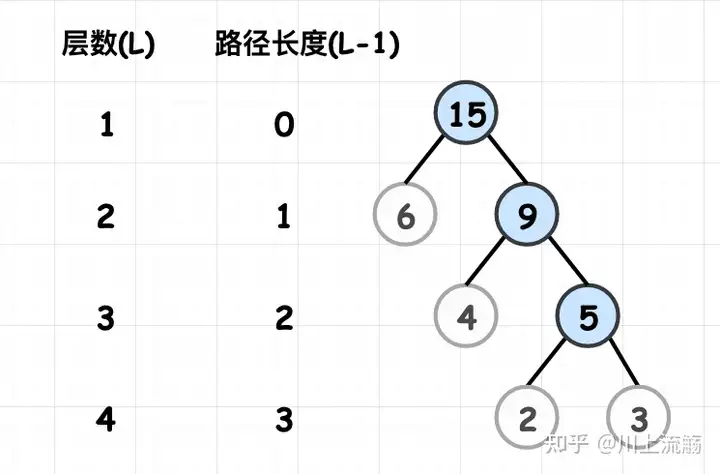
2️⃣ 节点的权和带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
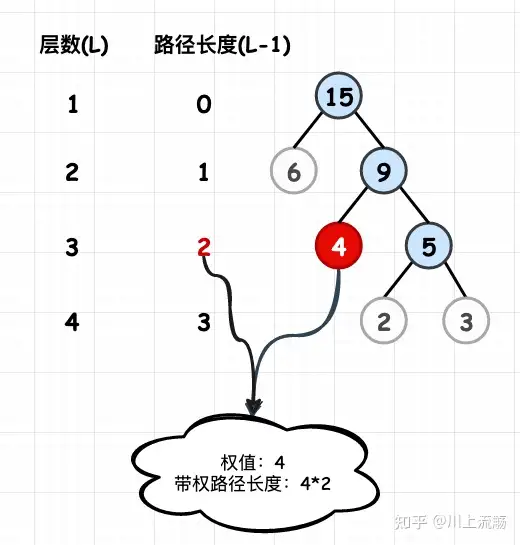
3️⃣ 树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
如上图:数的带权路径长度为:
WPL = (2+3) * 3 + 4 * 2 + 6 * 1 = 29
哈夫曼树的构造
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
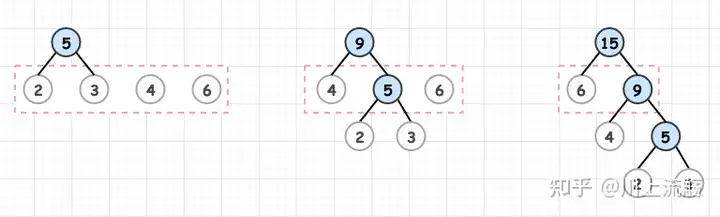
例如:对 2,3,4,6 这四个数进行构造
哈夫曼树的应用:哈夫曼编码
引言
哈夫曼编码的介绍
哈夫曼编码是一种压缩编码的编码算法,是基于哈夫曼树的一种编码方式。哈夫曼树又称为带权路径长度最短的二叉树。
哈夫曼编码跟 ASCII 编码有什么区别?ASCII 编码是对照ASCII 表进行的编码,每一个字符符号都有对应的编码,其编码长度是固定的。而哈夫曼编码对于不同字符的出现频率其使用的编码是不一样的。其会对频率较高的字符使用较短的编码,频率低的字符使用较高的编码。这样保证总体使用的编码长度会更少,从而实现到了数据压缩的目的。
举一个例子:对字符串“aaa bb cccc dd e”使用 ASCII 进行编码得到的结果为:97 97 97 32 98 98 32 99 99 99 99 32 100 100 32 101 (十进制)需要 16 个字节,如果使用二进制表示的话需要 128位的内存空间去存储。
而如果使用 Unicode 的话会更多,因为 Unicode 又称为万国码,内容更多,因此使用的空间也需要更大。
接下来使用哈夫曼编码对上面的字符串进行编码。看看需要多大的空间
统计频率
上面的介绍已经说明了哈夫曼编码会根据字符出现的频率从而条件字符使用的编码长度。因此要先求出这个字符串中每个字符出现的频率
| 字符 | c | ' ' 空 | a | b | d | e |
|---|---|---|---|---|---|---|
| 频率 | 4 | 4 | 3 | 2 | 2 | 1 |
构建哈夫曼树
排序
哈夫曼树是一个带权的二叉树,而在哈夫曼编码中,字符的出现频率就是字符的权重。因此要根据字符的频率放入优先队列中进行排序。然后根据这些字符构建一棵哈夫曼树
| 字符 | e | d | b | a | ' ' 空 | c |
|---|---|---|---|---|---|---|
| 频率 | 1 | 2 | 2 | 3 | 4 | 4 |
将队列中的每一个元素(字符)都看成一棵树。
合并
进行迭代,每次都去除队列中的前面两个元素,也就是权值最小的两棵子树进行合并成一棵子树。直到最终所有的元素合并成一棵树。这棵树就是哈夫曼树。
合并步骤
合并 1、2 权值为 3:
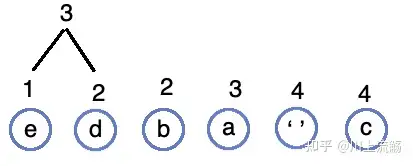
将 3这棵树重新插入队列:
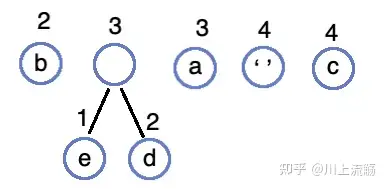
合并 2、3 生成 5 的树,并插入队列:
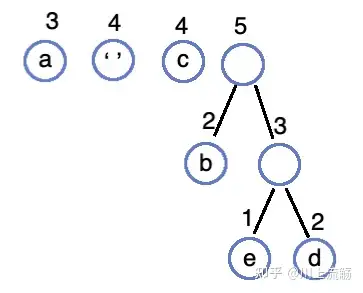
合并 3、4 生成 7 的树,并插入队列:
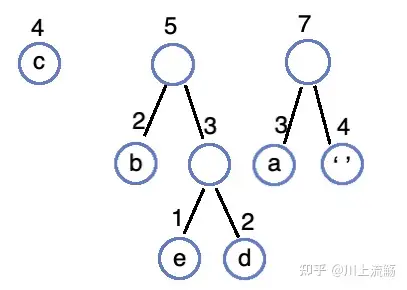
合并 4、5 生成 9 的数,并插入队列:
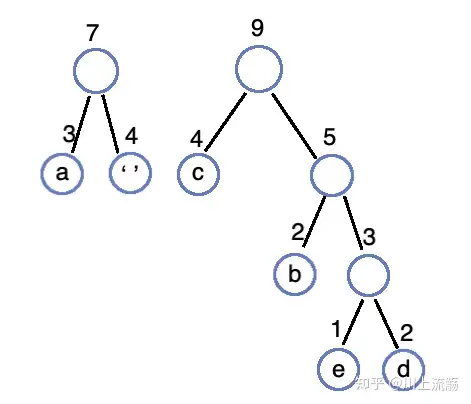
合并 7、9 生成 16 的树,最终只有一棵树,该树便是这个字符串所生成的哈夫曼树:
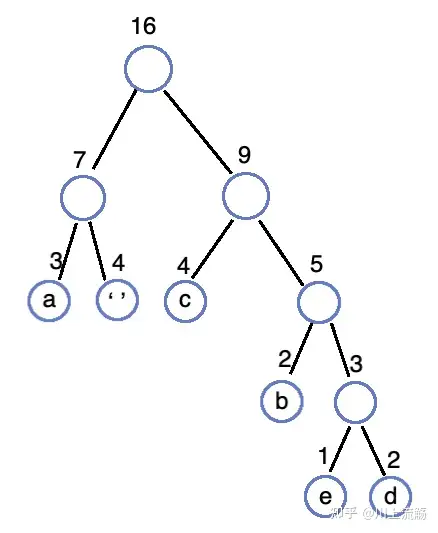
为哈夫曼树进行编码
将二叉树分支中的左分支编为 0,右分支编为 1:
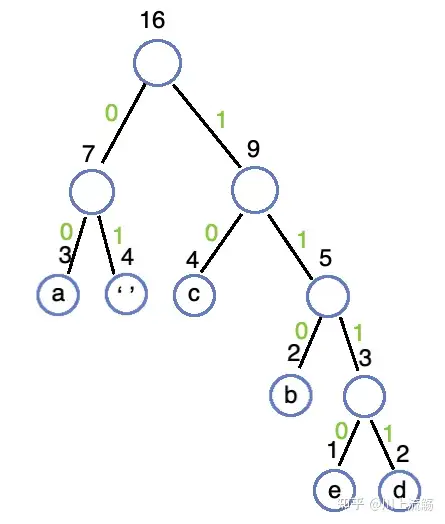
可以发现每个字符都在树的叶子节点上,因此要获取每个字符的哈夫曼编码,就通过根节点遍历到对应的子节点所经历的路径就是这个字符的编码:
| 字符 | d | e | b | a | ' ' | c |
|---|---|---|---|---|---|---|
| 编码 | 1111 | 1110 | 110 | 00 | 01 | 10 |
可以发现使用频率高的字符e 其编码长度是比出现频率低的字符c 编码长度要少。最后计算使用哈夫曼编码的字符串“aaa bb cccc dd e”要使用多少位的内存空间进行存储:出现次数 * 编码长度。结果为 4 * 3 + 3 * 2 + 11 * 2 = 40位,与 ASCII 对应的 128位,少了2/3的存储空间。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 单线程的Redis速度为什么快?
· 展开说说关于C#中ORM框架的用法!
· Pantheons:用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探
· 为什么 退出登录 或 修改密码 无法使 token 失效