zkw线段树总结

zkw线段树

学习一个快速的线段树还是很重要的，zkw线段树据说是简单有快速，但是无奈经常忘记，写个笔记记录一下。

zkw线段树的实质就是堆式存储，从上到下从1开始编号，就有父节点是n，那么子节点就是2*n和2*n+1。对于编号的二进制表示，我们有：

 

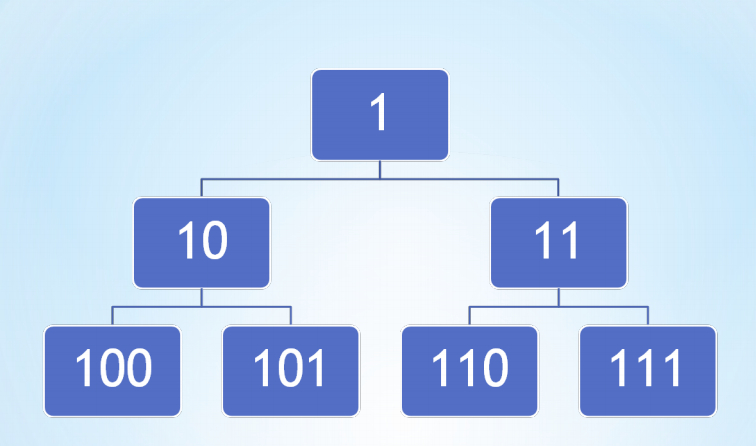
是不是发现了什么，那就是子节点右移一位（也就是除以二）就是父节点了，通过这样，我们就不用在递归求解了，直接采用for循环每次右移一位进行求解。

我们知道线段树的最底层就是原始的数据，上一层等于其所下两个子节点的和。我们造一个满二叉树，如果个数为2ⁿ-1，其中最底层就是2^n-1个，但是由于zkw线段树查询的是一个开区间值，所以实际上底层最左和最右的是不能存放东西的，所以如果原始个数最大为n个，那么我们就要让底层的个数至少为n+2个。

至于为什么最左最右不能放东西，原因是这样的：

　　我们在进行求解区间和的时候，如果某个非底层节点包括了该区间的某段的话，直接采用该节点的值作为求解就会变得简单，如果是闭区间且此时在该节点的父节点的右侧，那么在右移一位的时候该父节点因为包含了该节点的兄弟节点（也就是父节点的左侧）而变得不再是闭区间了，所以还不如直接开区间，那么该节点所在的位置一定不会包括在结果里面。对于左边界如果一开始节点在父节点的左侧，那么因为是开区间，右节点是包括在结果里面的，所以加上，如果左边界是在右侧，则说明该节点不是在区间内的（注，一开始是从底层开始，节点的值就是原始值），我们要的在对面树上，所以右移一位，这样对面树的父节点现在就是我们父节点的兄弟了，而且你现在也在父节点的父节点的左边了。右边界处理方法也是类似，但是是在右边加左边，因为左边才是区间内，可以参考下图和注解。

 

（求第1到第4的值，也就是闭区间【1，4】，开区间（0，5），箭头一开始指向8号位和13号位（因为最左最右不算，底层第一个就是9号位），发现8是左边，那么把右边加起来，13是右边，把左边加起来，我们现在就得到了第1个和第4个的值，两个箭头右移一位，到了4和6，4在左边，加上5，注意5代表的是第2和第3的值，而6号因为在左边，就不管，接着右移，2和3号，2号左边，3号右边，但是两个边界已经在同一个节点也就是1号节点下方了，所以终止了。）

对于边界，如果它在左边那么它的编号是个偶数，右边就是基数，那么我们可以通过（假设x，y为左右开边界）x&1，y&1判断，对于最后终止情况，x和y相差1，也就是x^y = 1的，我们判断如果(x^y)^1为0的话就截止。于是我们有查询子区间代码：

int query(int s, int e)//第s个到第e个的和
{
    int ans = 0;
    //M为偏移量，也就是2^(n-1)，因为上图的9号也是对于第一个，此时偏移量为8，【s+M，e+M】就是闭区间，开区间就（s+M-1，e+M+1）
    for(int x = s + M - 1, y = e + M + 1; x ^ y ^ 1; x >>= 1, y >>= 1)
    {
        if(~x & 1)//如果左边界在父节点的左边，对x取反，左边是偶数变成奇数，与1与得到1
            ans += T[x ^ 1];
        if(y & 1)
            ans += T[y ^ 1];
    }
    return ans;
}

对于修改单个的情况，我们不妨采用右移一位（即除以二）的方法修改其和其父节点，直到为0:

void change(int pos, int value)
{
    for(T[pos += M] = value, pos >>= 1; pos; pos >>= 1)//直到实际在线段树中的位置，修改其值，在找到它的父节点，直到父节点为0
    {
        T[pos] = T[2 * pos] + T[2 * pos + 1];//更新父节点
    }
}

对于区间修改

这种情况下我们要稍微改变一下，就是要引入一个查分思想，父节点的两个儿子，取其中最小的，两个儿子同减去这个值（结果就是一个为零，一个是正整数），父亲加上这个值，每次计算的时候都要从下加到上，才能得到答案，所以查询区间和单个的复杂度都是O(log_N)（原非差分做法中查询单个就是O(N)复杂度）

 

（未完待续）