(js描述的)数据结构[树结构1.2](12)
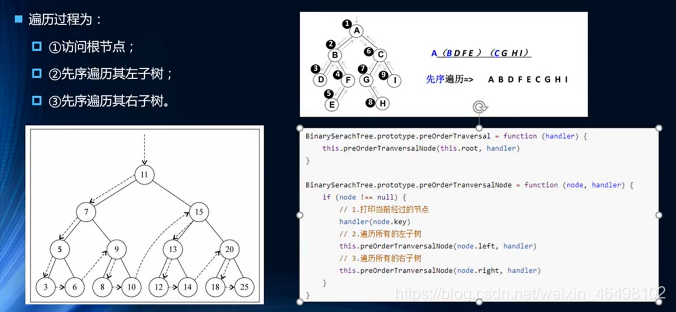
1.先序遍历
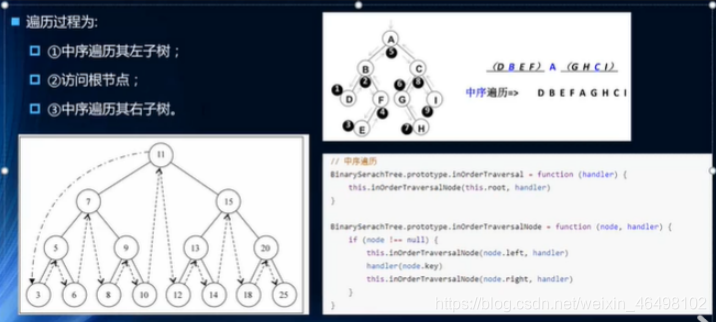
2.中序遍历
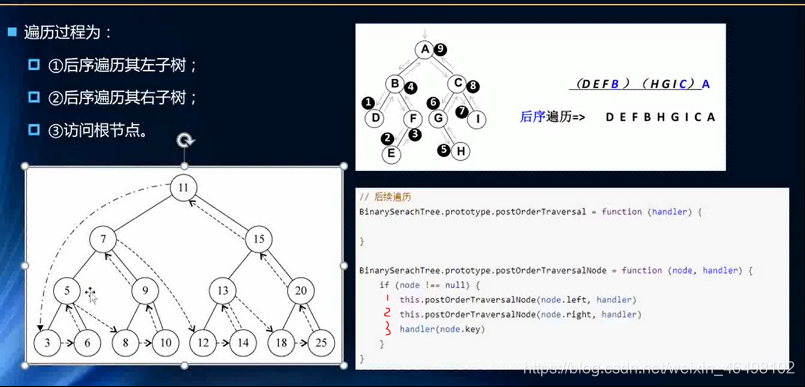
3.后序遍历
4.递归调用栈详解:
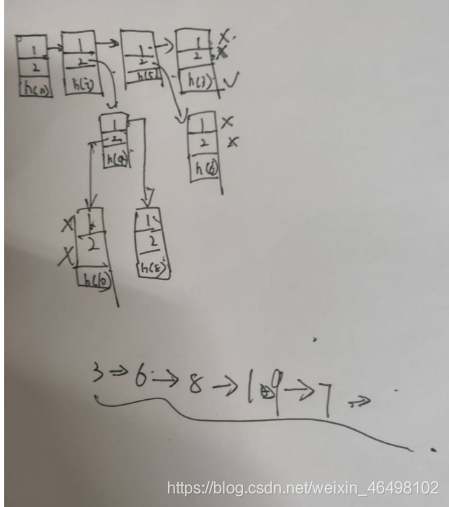
详细见: https://zhuanlan.zhihu.com/p/24291978
5.删除节点操作分析:
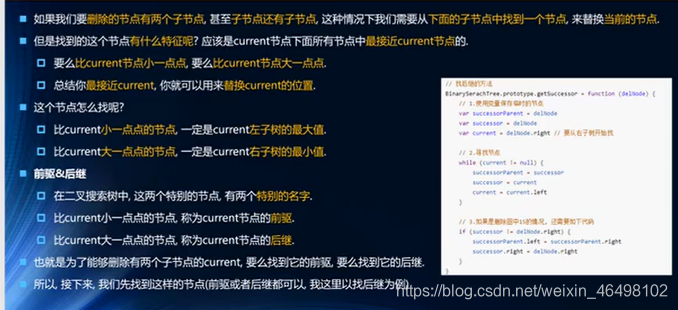
5.代码封装
//封装二叉搜索树
function BinarySearchTree() {
//封装节点内部类
function Node(key) {
this.key = key
this.left = null
this.right = null
}
//属性
this.root = null
//方法
// 1. insert方法
BinarySearchTree.prototype.insert = function(key) {
var newNode = new Node(key)
if (this.root == null) {
this.root = newNode
} else {
this.insertNode(this.root, newNode)
}
}
//封装一个递归方法
BinarySearchTree.prototype.insertNode = function(node, newNode) {
if (newNode.key > node.key) {
if (node.left == null) {
node.left = newNode
} else {
this.insertNode(node.left, newNode)
}
} else {
if (node.right == null) {
node.right = newNode
} else {
this.insertNode(node.right, newNode)
}
}
}
// 遍历方式
// 1. 先序遍历
BinarySearchTree.prototype.preOrderTranversal = function(handle) { //handle 为传入的处理key的函数
this.preOrderTranversalNode(this.ropot, handle)
}
//定义一个遍历节点的方法
BinarySearchTree.prototype.preOrderTranversalNode = function(node, handle) {
if (node !== null) {
handle(node.key)
// 先序遍历左节点
this.preOrderTranversalNode(node.left, handle)
//先序遍历右节点
this.preOrderTranversalNode(node.right, handle)
}
}
// 2.中序遍历
BinarySearchTree.prototype.midOrderTranversal = function(handle) { //handle 为传入的处理key的函数
this.midOrderTranversalNode(this.ropot, handle)
}
//定义一个遍历节点的方法
BinarySearchTree.prototype.midOrderTranversalNode = function(node, handle) {
if (node !== null) {
// 先序遍历左节点
this.midOrderTranversalNode(node.left, handle)
handle(node.key)
//先序遍历右节点
this.midOrderTranversalNode(node.right, handle)
}
}
// 3.后序遍历
BinarySearchTree.prototype.postOrderTranversal = function(handle) { //handle 为传入的处理key的函数
this.postOrderTranversalNode(this.ropot, handle)
}
//定义一个遍历节点的方法
BinarySearchTree.prototype.postOrderTranversalNode = function(node, handle) {
if (node !== null) {
// 先序遍历左节点
this.postOrderTranversalNode(node.left, handle)
//先序遍历右节点
this.postOrderTranversalNode(node.right, handle)
handle(node.key)
}
}
// 寻找最值
// 最大值
BinarySearchTree.prototype.max = function() {
var node = this.root
while (node.right !== null) {
node = node.right
}
return node.key
}
// 最小值
BinarySearchTree.prototype.min = function() {
var node = this.root
while (node.left !== null) {
node = node.left
}
return node.key
}
//搜索特定key
BinarySearchTree.prototype.search = function(key) {
// 1.通过循环实现
var node =this.root
while (node !== null) {
if (node.key < key ) {
node = node.right
} else if(node.key > key) {
node = node.left
} else {
return true
}
return false
}
// 2.通过递归实现
this.searchNode(this.root)
}
//递归函数封装
BinarySearchTree.prototype.searchNode = function(node, key) {
if (node == null) {
return false
}
if (node.key < key) {
this.searchNode(node.left)
} else if(node.key > key) {
this.searchNode(node.right)
} else {
return true
}
}
//删除操作
BinarySearchTree.prototype.remove = function(key) {
var current = this.root
var parent = null
var isLeftChild = true
//寻找key对应的节点
while (current.key != key) {
parent = current
if (current.key < key) {
isLeftChild = true
current = current.right
} else {
isLeftChild = false
current = current.left
}
if (current == null) {
return false
}
}
//找到了key对应的节点
// 删除的节点是叶子节点
if(current.left == null && current.right == null) {
//是根节点
if(current == this.root) {this.root = null}
//
else { isLeftChild ? parent.left = null: parent.right =null}
}
//节点有一个子节点
else if (current.left == null || current.right == null) {
//当前删除的节点是父节点的左节点
if (current == this.root) { this.root = current.left || current.right}
else if (isLeftChild) {
parent.left = current.left || current.right
}
//当前删除的节点是父节点的右节点
else{
parent.right = current.right || current.left
}
}
//节点有两个子节点
else {
var successor = this.getSuccessor(current)
if (successor == this.root) {
this.root = successor
} else {
if (isLeftChild) {
parent.left = successor
} else {
parent.right = successor
}
}
successor.left = current.left
}
}
//寻找后继的方法
BinarySearchTree.prototype.getSuccessor = function(delNode) {
var successor = delNode //后继节点的父节点
var current = delNode.right //后继节点的子节点
var successorParent = delNode //后继节点
while (current != null) {
successorParent = successor
successor = current
current = current.left
}
if (successor != delNode.right) { //当后继节点的不是删除节点的右节点时
successorParent.left = successor.right //把后记节点的右节点让后继节点的父节点的left指向它
successor.right = delNode.right //、把后继节点的右节点接上删除节点的右节点
}
return successor
}
}
删除操作总结:

感谢您花时间阅读此篇文章,如果您觉得看了这篇文章之后心情还比较高兴,可以打赏一下,请博主喝上一杯咖啡,让博主继续码字……
本文版权归作者和博客园共有,来源网址:https://blog.csdn.net/weixin_46498102 欢迎各位转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接


 浙公网安备 33010602011771号
浙公网安备 33010602011771号