隐马尔可夫模型

原文地址：http://www.cnblogs.com/jacklu/p/6225073.html

1 概述

隐马尔可夫模型（Hidden Markov Model，HMM）是结构最简单的动态贝叶斯网，这是一种著名的有向图模型，主要用于时序数据建模（语音识别、自然语言处理等）。

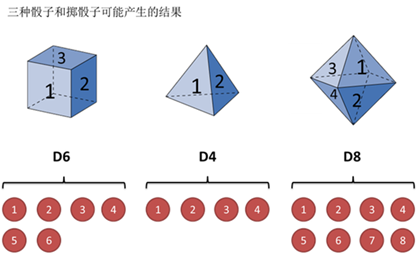
假设有三个不同的骰子（6面、4面、8面），每次先从三个骰子里选一个，每个骰子选中的概率为，如下图所示，重复上述过程，得到一串数字[1 6 3 5 2 7]。这些可观测变量组成可观测状态链。

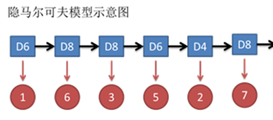
同时，在隐马尔可夫模型中还有一条由隐变量组成的隐含状态链，在本例中即骰子的序列。比如得到这串数字骰子的序列可能为[D6 D8 D8 D6 D4 D8]。

 

隐马尔可夫模型示意图如下所示：

 

图中，箭头表示变量之间的依赖关系。在任意时刻，观测变量（骰子点数）仅依赖于状态变量（哪类骰子），“观测独立性假设”。

同时，。这就是马尔可夫链，即系统的下一时刻的状态仅由当前状态决定不依赖以往的任何状态（无记忆性），“齐次马尔可夫性假设”。

 

2 隐马尔可夫模型三要素

对于一个隐马尔可夫模型，它的所有N个可能的状态的集合，所有M个可能的观测集合

隐马尔可夫模型三要素：

状态转移概率矩阵A， 下一时刻t+1状态为的概率

观测概率矩阵B，，生成观测值的概率

初始状态概率向量π，

一个隐马尔可夫模型可由λ=(A, B, π)来指代。

 

3 隐马尔可夫模型的三个基本问题

（1） 给定模型λ=(A, B, π)，计算其产生观测序列的概率P(O|λ)；

计算掷出点数163527的概率

（2） 给定模型λ=(A, B, π)和观测序列，推断能够最大概率产生此观测序列的状态序列，即使P(I|O)最大的I；

推断掷出点数163527的骰子种类

（3） 给定观测序列，估计模型λ=(A, B, π)的参数，使P(O|λ)最大；

已知骰子有几种，不知道骰子的种类，根据多次掷出骰子的结果，反推出骰子的种类

 

这三个基本问题在现实应用中非常重要，例如根据观测序列推测当前时刻最有可能出现的观测值，这就转换成基本问题（1）；

在语音识别中，观测值为语音信号，隐藏状态为文字，根据观测信号推断最有可能的状态序列，即基本问题(2)；

在大多数应用中，人工指定参数模型已变得越来越不可行，如何根据训练样本学得最优参数模型，就是基本问题(3)。

 

4 三个基本问题的解法

基于两个条件独立假设，隐马尔可夫模型的这三个基本问题均能被高效求解。

4.1 基本问题（1）解法

4.1.1 直接计算法(概念上可行，计算上不可行)

通过列举所有可能的长度为T的状态序列，求各个状态序列I与观测序列O同时出现的联合概率P(I,O|λ)，然后对所有可能求和得到P(O|λ)。

状态序列的概率是P(I|λ)=

对于固定状态序列 I，观测序列的概率P(O|I,λ)=

I 和 O同时出现的联合概率P(I,O|λ)= P(I|λ) P(O|I,λ)

然后对所有可能的 I 求和，得到P(O|λ)

这种方法计算量很大，算法不可行。

4.1.2 前向算法(t=1,一步一步向前计算)

前向概率，表示模型λ，时刻 t，观测序列为且状态为的概率。

（1） 初始化前向概率

状态为和观测值为的联合概率

（2） 递推t=1,2,…,T-1

根据下图，得到

（3） 终止

前向算法高效的关键是其局部计算前向概率，根据路径结构，如下图所示，每次计算直接利用前一时刻计算结果，避免重复计算，减少计算量。

4.1.3 后向算法

（1）初始化后向概率

（2）递推t=T-1,T-2,…,1

（4） 终止

前向算法高效的关键是其局部计算前向概率，根据路径结构，如下图所示，每次计算直接利用前一时刻计算结果，避免重复计算，减少计算量。

4.2 基本问题（2）解法

4.2.1 近似算法

选择每一时刻最有可能出现的状态，从而得到一个状态序列。这个方法计算简单，但是不能保证整个状态序列的出现概率最大。因为可能出现转移概率为0的相邻状态。

4.2.2 Viterbi算法

使用动态规划求解概率最大（最优）路径。t=1时刻开始，递推地计算在时刻t状态为i的各条部分路径的最大概率，直到计算到时刻T，状态为i的各条路径的最大概率，时刻T的最大概率即为最优路径的概率，最优路径的节点也同时得到。

如果还不明白，看一下李航《统计学习方法》的186-187页的例题就能明白算法的原理。

状态[3 3 3]极为概率最大路径。

4.3 基本问题（3）解法

4.3.1 监督学习方法

给定S个长度相同的（观测序列，状态序列）作为训练集，使用极大似然估计法来估计模型参数。

转移概率 的估计:样本中t时刻处于状态i，t+1时刻转移到状态j的频数为，则

观测概率和初始状态概率的估计类似。

4.3.2 Baum-Welch算法

使用EM算法得到模型参数估计式

EM算法是常用的估计参数隐变量的利器，它是一种迭代方法，基本思想是：

（1） 选择模型参数初始值；

（2） (E步)根据给定的观测数据和模型参数，求隐变量的期望；

（3） (M步)根据已得隐变量期望和观测数据，对模型参数做极大似然估计，得到新的模型参数，重复第二步。

 

参考资料：

《机器学习》周志华

《统计学习方法》李航

如何用简单易懂的例子解释隐马尔可夫模型https://www.zhihu.com/question/20962240