TSP问题(旅行商问题)[分支限界法]
问题:
旅行商从 a 开始周游下图所有的城市一次,然后回到 a,城市之间的旅行代价在图中标明。
请选择一个最优的行走顺序使得周游所有城市的代价最小。

思路:
随便怎么周游,对于一个城市来说,一定有一条进的路和一条出的路。
对于每个城市来说,暂时都选取代价最小的两条路来作为理想的路线,就算这些路不合理。
比如对于 a 来说,选择 a<->c(1) & a<->b(3) ;对于 e 来说,选择 e<->c(2) & e<->d(3)。
把所有的这些值加起来除以2,
本题即 lb=[(a<->c+a<->b)+(b<->a+b<->c)+(c<->a+c<->e)+(d<->e+d<->c)+(e<->c+e<->d)]/2=[(1+3)+(3+6)+(1+2)+(3+4)+(2+3)]/2=14 .
把这个值当成是理想的最小代价,然后接下来搜索解空间树的时候,都在该基础上进行。
下面画出搜索解空间树的过程,其中方框上面的是点的名称,下面是假设的理想周游代价,方框头顶是搜索顺序:
刚开始从 a 走
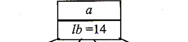
从 a 可以到达 b、c、d、e,
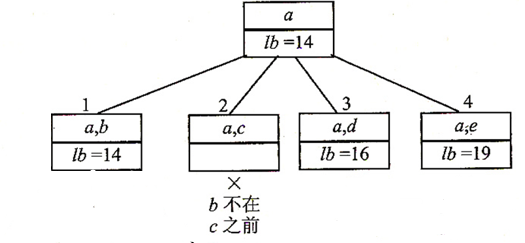
这里有一个小细节,就是图中的 2 节点。想想如果周游路线 a<->b<->d<->e<->a 和 a<->e<->d<-><->c<->b<->a ,这两条路线其实是一样的,但是如果不加处理的话,可能两条路线会在搜索的时候都被搜索过,这样浪费了时间。因此,我们这里做个小约定,约定 b 要在 c 之前出现。因此,图中节点 2 就被抛弃了。
继续上面的,从 a 走到那些点后,怎么计算理想代价呢,也就是说怎么计算 lb 呢。
我们用 a 到 d 来举例子吧。
最开始 lb 是选取每个点的代价最小的两条路, lb=[(a<->c+a<->b)+(b<->a+b<->c)+(c<->a+c<->e)+(d<->e+d<->c)+(e<->c+e<->d)]/2。a 走的是c 和 b 这两个,d 走的是e 和 c 。
现在我们选择 a<->d ,那 d 的一条路要被改成 a 了。我们选择将原来的 a<->b 改成 a<->d,因为要使代价最小,所以选择代价大的来替换。那么 d<->c 就被替换成 d<->a了。这时再计算就可以得到新的 lb 了。
我们应该选择 lb 最小的往下搜索,较大的等下再搜索。于是
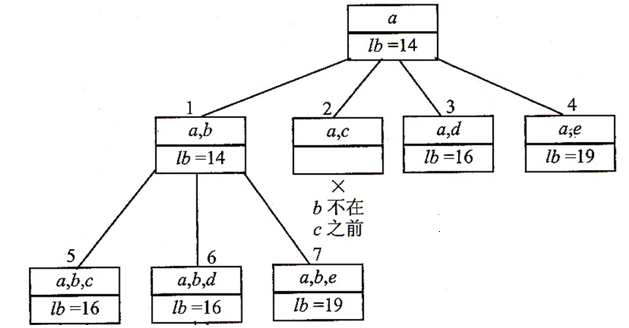
继续向下
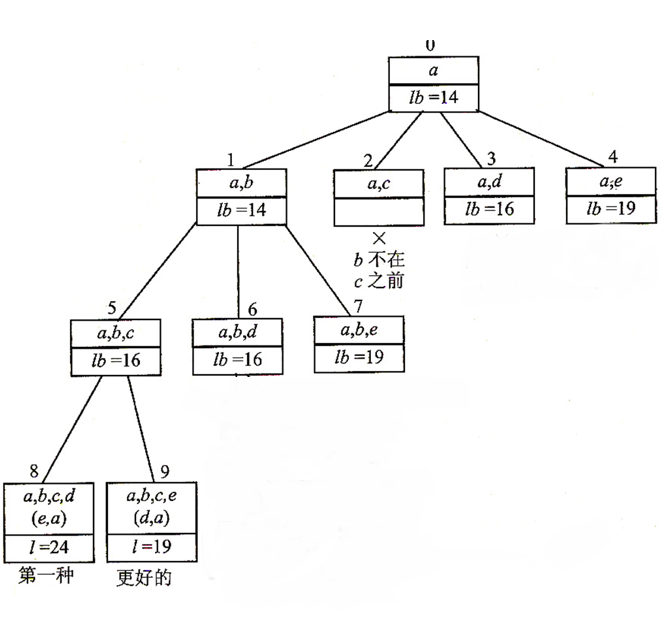
这时已经找出两个周游路程了(因为最后肯定要回到 a 就没向下画了),我们继续搜索,看看有没再好点的解。向上退一层,就是 节点 6 了,所以
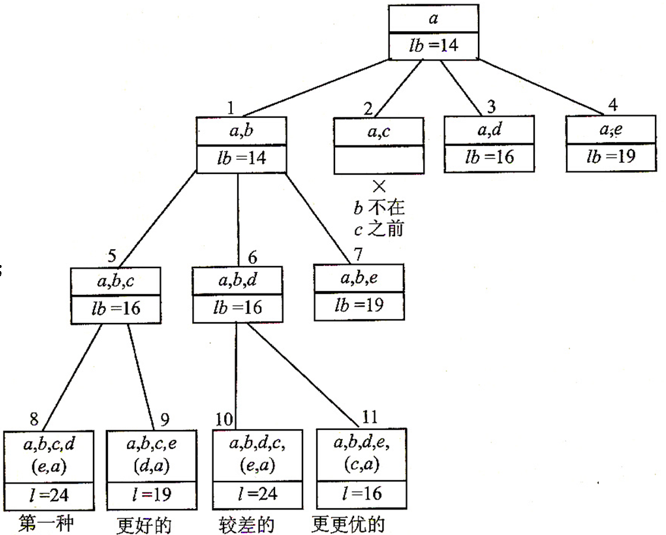
继续搜索,发现节点 7 才走到 e 就要 19,而 节点 11 走完了只需要 16,所以把它抛弃,继续退回,发现 3,4 都不行
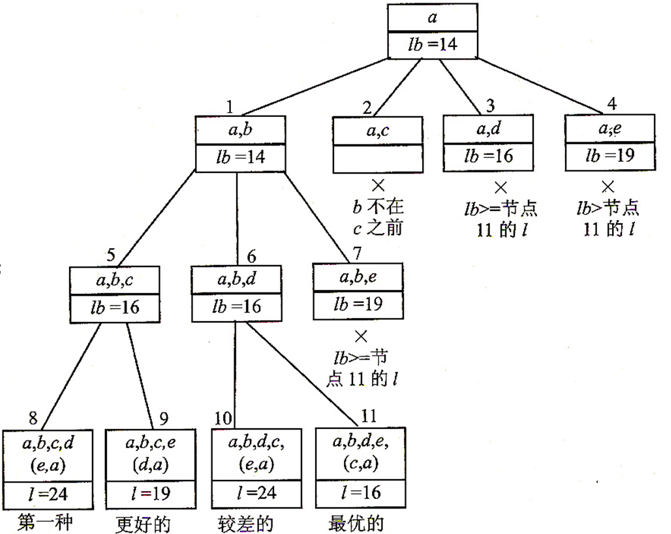
得到了最优解。
代码:
代码我不会写,哈哈哈哈哈哈哈哈哈。。。。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步