R语言实战学习笔记-基本统计分析
本文主要介绍以下内容:1.基本统计方法 2频数表和列联表 3.相关 4.t检验 5.组间差异的非参数检验
1.基本统计方法
简单实例
mycars<-c("mpg","hp","wt")
summary(mtcars[mycars])
结果:
mpg hp wt
Min. :10.40 Min. : 52.0 Min. :1.513
1st Qu.:15.43 1st Qu.: 96.5 1st Qu.:2.581
Median :19.20 Median :123.0 Median :3.325
Mean :20.09 Mean :146.7 Mean :3.217
3rd Qu.:22.80 3rd Qu.:180.0 3rd Qu.:3.610
Max. :33.90 Max. :335.0 Max. :5.424
summary()函数提供了最小值、最大值、四分位数、均值,另外还可以因子向量和逻辑型向量的频数统计。另有apply()函数和sapply()函数计算所选择的任意描述性统计量。对于sapply(x)函数,使用格式如下:
sapply(x,FUN,options)
其中x是数据框,FUN作为一个任意函数。如果指定了options,他们将被传递给FUN。可以插入的函数有mean()、sd()、var()、min()、max()、median()、length()、range()、quantile()。函数fivenum()可返回图基五数总括(最小值,下四分位数、中位数、上四分位数、最大值)
mystats <- function(x, na.omit=FALSE){
if (na.omit)
x <- x[!is.na(x)]
m <- mean(x)
n <- length(x)
s <- sd(x)
skew <- sum((x-m)^3/s^3)/n
kurt <- sum((x-m)^4/s^4)/n - 3
return(c(n=n, mean=m, stdev=s, skew=skew, kurtosis=kurt))
}
myvars<-c("mpg","hp","wt")
sapply(mtcars[myvars],mystats)
#输出值
mpg hp wt
n 32.000000 32.0000000 32.00000000
mean 20.090625 146.6875000 3.21725000
stdev 6.026948 68.5628685 0.97845744
skew 0.610655 0.7260237 0.42314646
kurtosis -0.372766 -0.1355511 -0.02271075
其他描述性统计函数,包含Hmisc、pastecs、psych。
library(Hmisc)
myvars<-c("mpg","hp","wt")
describe(mtcars[myvars])
#输出结果
3 Variables 32 Observations
--------------------------------------------------------------------
mpg
n missing distinct Info Mean Gmd .05
32 0 25 0.999 20.09 6.796 12.00
.10 .25 .50 .75 .90 .95
14.34 15.43 19.20 22.80 30.09 31.30
lowest : 10.4 13.3 14.3 14.7 15.0, highest: 26.0 27.3 30.4 32.4 33.9
--------------------------------------------------------------------
hp
n missing distinct Info Mean Gmd .05
32 0 22 0.997 146.7 77.04 63.65
.10 .25 .50 .75 .90 .95
66.00 96.50 123.00 180.00 243.50 253.55
lowest : 52 62 65 66 91, highest: 215 230 245 264 335
--------------------------------------------------------------------
wt
n missing distinct Info Mean Gmd .05
32 0 29 0.999 3.217 1.089 1.736
.10 .25 .50 .75 .90 .95
1.956 2.581 3.325 3.610 4.048 5.293
lowest : 1.513 1.615 1.835 1.935 2.140, highest: 3.845 4.070 5.250 5.345 5.424
--------------------------------------------------------------------
library(pastecs)
myvars<-c("mpg","hp","wt")
stat.desc(mtcars[myvars])
#输出结果
mpg hp wt
nbr.val 32.0000000 32.0000000 32.0000000
nbr.null 0.0000000 0.0000000 0.0000000
nbr.na 0.0000000 0.0000000 0.0000000
min 10.4000000 52.0000000 1.5130000
max 33.9000000 335.0000000 5.4240000
range 23.5000000 283.0000000 3.9110000
sum 642.9000000 4694.0000000 102.9520000
median 19.2000000 123.0000000 3.3250000
mean 20.0906250 146.6875000 3.2172500
SE.mean 1.0654240 12.1203173 0.1729685
CI.mean.0.95 2.1729465 24.7195501 0.3527715
var 36.3241028 4700.8669355 0.9573790
std.dev 6.0269481 68.5628685 0.9784574
coef.var 0.2999881 0.4674077 0.3041285
library(psych)
myvars<-c("mpg","hp","wt")
describe(mtcars[myvars])
#输出结果
vars n mean sd median trimmed mad min max range
mpg 1 32 20.09 6.03 19.20 19.70 5.41 10.40 33.90 23.50
hp 2 32 146.69 68.56 123.00 141.19 77.10 52.00 335.00 283.00
wt 3 32 3.22 0.98 3.33 3.15 0.77 1.51 5.42 3.91
skew kurtosis se
mpg 0.61 -0.37 1.07
hp 0.73 -0.14 12.12
wt 0.42 -0.02 0.17
分组描述性统计量:在比较多组个体或观测时,关注的焦点经常是各组的描述性统计信息,而不是样本整体的描述性统计信息,
myvars<-c("mpg","hp","wt") aggregate(mtcars[myvars],by=list(am=mtcars$am),mean) #输出结果 am mpg hp wt 1 0 17.14737 160.2632 3.768895 2 1 24.39231 126.8462 2.411000
#aggregate()仅允许在每次调用中使用平均值、标准差这样的单返回值函数
#by(data,INDICES,FUN)
dstats<-function(x){sapply(x,mystats)
myvars<-c("mpg","hp","wt")
by(mtcars[myvars],mtcars$am,dstats)
mtcars$am: 0
mpg hp wt
n 19.00000000 19.00000000 19.0000000
mean 17.14736842 160.26315789 3.7688947
stdev 3.83396639 53.90819573 0.7774001
skew 0.01395038 -0.01422519 0.9759294
kurtosis -0.80317826 -1.20969733 0.1415676
--------------------------------------------------------------------
mtcars$am: 1
mpg hp wt
n 13.00000000 13.0000000 13.0000000
mean 24.39230769 126.8461538 2.4110000
stdev 6.16650381 84.0623243 0.6169816
skew 0.05256118 1.3598859 0.2103128
kurtosis -1.45535200 0.5634635 -1.1737358
分组计算的扩展,doBy包和psych包提供了分组计算的描述性统计量的函数,doBy包中的summaryBy()函数使用的基本格式:
#doBy()包中summaryBy()函数的使用格式:
#summaryBy(formula,data=dataframe,FUN=function)
#formula接受以下格式:
#var1+var2+var3+var4+……+varN~groupvar1+groupvar2+……#+groupvarN
#在~左侧的变量师需要分析的数值型变量,而在右侧的变量是类别型的分组变#量。
library(doBy)
summaryBy(mpg+hp+wt~am,data=mtcars,FUN=mystats)
#输出结果
am mpg.n mpg.mean mpg.stdev mpg.skew mpg.kurtosis hp.n hp.mean hp.stdev hp.skew
1 0 19 17.14737 3.833966 0.01395038 -0.8031783 19 160.2632 53.90820 -0.01422519
2 1 13 24.39231 6.166504 0.05256118 -1.4553520 13 126.8462 84.06232 1.35988586
hp.kurtosis wt.n wt.mean wt.stdev wt.skew wt.kurtosis
1 -1.2096973 19 3.768895 0.7774001 0.9759294 0.1415676
2 0.5634635 13 2.411000 0.6169816 0.2103128 -1.1737358
library(psych)
myvars<-c("mpg","hp","wt")
describeBy(mtcars[myvars],list(am=mtcars$am))
#输出结果
Descriptive statistics by group
am: 0
vars n mean sd median trimmed mad min max range skew kurtosis se
mpg 1 19 17.15 3.83 17.30 17.12 3.11 10.40 24.40 14.00 0.01 -0.80 0.88
hp 2 19 160.26 53.91 175.00 161.06 77.10 62.00 245.00 183.00 -0.01 -1.21 12.37
wt 3 19 3.77 0.78 3.52 3.75 0.45 2.46 5.42 2.96 0.98 0.14 0.18
--------------------------------------------------------------------
am: 1
vars n mean sd median trimmed mad min max range skew kurtosis se
mpg 1 13 24.39 6.17 22.80 24.38 6.67 15.00 33.90 18.90 0.05 -1.46 1.71
hp 2 13 126.85 84.06 109.00 114.73 63.75 52.00 335.00 283.00 1.36 0.56 23.31
wt 3 13 2.41 0.62 2.32 2.39 0.68 1.51 3.57 2.06 0.21 -1.17 0.17
2.频数表和列联表
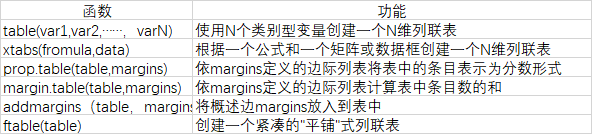
#一维列联表
#table()函数生成简单的频数统计表
library(vcd)
mytable<-with(Arthritis,table(Improved))
mytable
#输出结果
Improved
None Some Marked
42 14 28
#prop.table()将频数转化成比例值:
prop.table(mytable)
Improved
None Some Marked
0.5000000 0.1666667 0.3333333
#prop.table()*100转化成百分比
prop.table(mytable)*100
Improved
None Some Marked
50.00000 16.66667 33.33333
#二维列联表
#table()函数的使用格式
#mytable<-table(A,B) A为行变量 B为列变量
#xtabs()函数还可以使用公式风格的输入创建列联表
#mytable<-xtabs(~A+B,data=mydata)
#其中mydata是一个矩阵或者数据框
library(vcd)
mytable<-xtabs(~Treatment+Improved,data=Arthritis)
mytable
#输出结果
Improved
Treatment None Some Marked
Placebo 29 7 7
Treated 13 7 21
#margin.table()和prop.table()函数生成频数和比例
margin.table(mytable,1)
#输出结果
Treatment
Placebo Treated
43 41
prop.table(mytable,1)
#输出结果
Improved
Treatment None Some Marked
Placebo 0.6744186 0.1627907 0.1627907
Treated 0.3170732 0.1707317 0.5121951
#1代表table()语句中的第一个变量
#列和列比例的计算
margin.table(mytable,2)
Improved
None Some Marked
42 14 28
prop.table(mytable,2)
Improved
Treatment None Some Marked
Placebo 0.6904762 0.5000000 0.2500000
Treated 0.3095238 0.5000000 0.7500000
#addmargins()函数为表增加边际和
addmargins(mytable)
Improved
Treatment None Some Marked Sum
Placebo 29 7 7 43
Treated 13 7 21 41
Sum 42 14 28 84
addmargins(prop.table(mytable))
Improved
Treatment None Some Marked Sum
Placebo 0.34523810 0.08333333 0.08333333 0.51190476
Treated 0.15476190 0.08333333 0.25000000 0.48809524
Sum 0.50000000 0.16666667 0.33333333 1.00000000
addmargins(prop.table(mytable,1),2)
#只增加了行的和
Improved
Treatment None Some Marked Sum
Placebo 0.6744186 0.1627907 0.1627907 1.0000000
Treated 0.3170732 0.1707317 0.5121951 1.0000000
addmargins(prop.table(mytable,2),1)
#只增加列的和
Improved
Treatment None Some Marked
Placebo 0.6904762 0.5000000 0.2500000
Treated 0.3095238 0.5000000 0.7500000
Sum 1.0000000 1.0000000 1.0000000
#使用CrossTable()创建二维列表
library(gmodels)
CrossTable(Arthritis$Treatment,Arthritis$Improved)
Cell Contents
|-------------------------|
| N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 84
| Arthritis$Improved
Arthritis$Treatment | None | Some | Marked | Row Total |
--------------------|-----------|-----------|-----------|-----------|
Placebo | 29 | 7 | 7 | 43 |
| 2.616 | 0.004 | 3.752 | |
| 0.674 | 0.163 | 0.163 | 0.512 |
| 0.690 | 0.500 | 0.250 | |
| 0.345 | 0.083 | 0.083 | |
--------------------|-----------|-----------|-----------|-----------|
Treated | 13 | 7 | 21 | 41 |
| 2.744 | 0.004 | 3.935 | |
| 0.317 | 0.171 | 0.512 | 0.488 |
| 0.310 | 0.500 | 0.750 | |
| 0.155 | 0.083 | 0.250 | |
--------------------|-----------|-----------|-----------|-----------|
Column Total | 42 | 14 | 28 | 84 |
| 0.500 | 0.167 | 0.333 | |
--------------------|-----------|-----------|-----------|-----------|
#多维列联表
mytable<-xtabs(~Treatment+Sex+Improved,data=Arthritis)
mytable
#输出结果
, , Improved = None
Sex
Treatment Female Male
Placebo 19 10
Treated 6 7
, , Improved = Some
Sex
Treatment Female Male
Placebo 7 0
Treated 5 2
, , Improved = Marked
Sex
Treatment Female Male
Placebo 6 1
Treated 16 5
#
ftable(mytable)
Improved None Some Marked
Treatment Sex
Placebo Female 19 7 6
Male 10 0 1
Treated Female 6 5 16
Male 7 2 5
#边际频数
margin.table(mytable,1)
Treatment
Placebo Treated
43 41
margin.table(mytable,2)
Sex
Female Male
59 25
margin.table(mytable,3)
Improved
None Some Marked
42 14 28
#治疗情况*改善情况的边际频数
margin.table(mytable,c(1,3))
Improved
Treatment None Some Marked
Placebo 29 7 7
Treated 13 7 21
#治疗情况*性别的各类改善情况说明
ftable(prop.table(mytable,c(1,2)))
Improved None Some Marked
Treatment Sex
Placebo Female 0.59375000 0.21875000 0.18750000
Male 0.90909091 0.00000000 0.09090909
Treated Female 0.22222222 0.18518519 0.59259259
Male 0.50000000 0.14285714 0.35714286
ftable(addmargins(prop.table(mytable,c(1,2)),3))
Improved None Some Marked Sum
Treatment Sex
Placebo Female 0.59375000 0.21875000 0.18750000 1.00000000
Male 0.90909091 0.00000000 0.09090909 1.00000000
Treated Female 0.22222222 0.18518519 0.59259259 1.00000000
Male 0.50000000 0.14285714 0.35714286 1.00000000
下面介绍三种检验:1.卡方独立检验 2.Fisher精确检验 3.Cochran-Mantel-Haenszel检验
#卡方独立性检验 library(vcd) #治疗情况与改善情况 mytable<-xtabs(~Treatment+Improved,data=Arthritis) chisq.test(mytable) #结果 data: mytable X-squared = 13.055, df = 2, p-value = 0.001463 #性别和改善情况 mytable<-xtabs(~Improved+Sex,data=Arthritis) chisq.test(mytable) #结果 data: mytable X-squared = 4.8407, df = 2, p-value = 0.08889 #(p<0.01说明治疗和改善有某种关系,p>0.05说明性别和改善效果没有关系) #Fisher精确检验 mytable<-xtabs(~Treatment+Improved,data=Arthritis) fisher.test(mytable) #结果 data: mytable p-value = 0.001393 alternative hypothesis: two.sided #备注:fisher.test()函数可以在任意行列数大于2的二维列联表中使用,但是不能用于2*2的列联表 #Cochran-Mantel-Haenszel检验 #mantelhaen.test()函数用于Cochran-Mantel-Haenszel卡方检验 #检验治疗情况和GIA是你情况在性别的每一水平下是否独立 mytable<-xtabs(~Treatment+Improved+Sex,data=Arthritis) mantelhaen.test(mytable) data: mytable Cochran-Mantel-Haenszel M^2 = 14.632, df = 2, p-value = 0.0006647 #结果表明,患者接受的治疗和得到的改善在性别的每一个水平小并不独立(分性别来看,用药治疗的患者较接受安慰剂的患者有了更好的改善) #相关性的度量 library(vcd) mytable<-xtabs(~Treatment+Improved,data=Arthritis) assocstats(mytable) #结果 X^2 df P(> X^2) Likelihood Ratio 13.530 2 0.0011536 Pearson 13.055 2 0.0014626 Phi-Coefficient : NA Contingency Coeff.: 0.367 Cramer's V : 0.394
3.相关
相关系数可以用来描述定量变量之间的关系。相关系数的符号(+-)表明关系的方向,其值的大小表示关系的强弱程度。
R可以计算多种相关系数,包括Pearson相关系数、Spearman相关系数、Kendall相关系数、偏相关系数、多分格相关系数和多系列相关系数
#1.Pearson、Spearman和Kendal相关
#Pearson积差相关系数衡量两个变量之间的线型相关程度
#Spearman等级相关系数则衡量分级定序变量之间的相关程度
#Kendal's Tau相关系数也是一种非参数等级相关度量
#cor()函数计算这三种相关系数,而cov()函数可以用来计算协方差
#cor(x,use=,method=)
#x 矩阵或者数据框
#use 指定趋势值的处理方式 all.obs-遇到缺失值报错、everything-遇到确实数据时,相关系数的计算结果将被设定为missing、complete.obs-行删除、pairwise.complete.obs-成对删除
states<-state.x77[,1:6]
#计算方差和协方差
cov(states)
#输出结果
Population Income Illiteracy Life Exp Murder HS Grad
Population 19931683.7588 571229.7796 292.8679592 -407.8424612 5663.523714 -3551.509551
Income 571229.7796 377573.3061 -163.7020408 280.6631837 -521.894286 3076.768980
Illiteracy 292.8680 -163.7020 0.3715306 -0.4815122 1.581776 -3.235469
Life Exp -407.8425 280.6632 -0.4815122 1.8020204 -3.869480 6.312685
Murder 5663.5237 -521.8943 1.5817755 -3.8694804 13.627465 -14.549616
HS Grad -3551.5096 3076.7690 -3.2354694 6.3126849 -14.549616 65.237894
#计算Pearson积差相关系数
cor(states)
#输出结果
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00000000 0.2082276 0.1076224 -0.06805195 0.3436428 -0.09848975
Income 0.20822756 1.0000000 -0.4370752 0.34025534 -0.2300776 0.61993232
Illiteracy 0.10762237 -0.4370752 1.0000000 -0.58847793 0.7029752 -0.65718861
Life Exp -0.06805195 0.3402553 -0.5884779 1.00000000 -0.7808458 0.58221620
Murder 0.34364275 -0.2300776 0.7029752 -0.78084575 1.0000000 -0.48797102
HS Grad -0.09848975 0.6199323 -0.6571886 0.58221620 -0.4879710 1.00000000
#计算Spearman等级相关系数
cor(states,method="spearman")
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.0000000 0.1246098 0.3130496 -0.1040171 0.3457401 -0.3833649
Income 0.1246098 1.0000000 -0.3145948 0.3241050 -0.2174623 0.5104809
Illiteracy 0.3130496 -0.3145948 1.0000000 -0.5553735 0.6723592 -0.6545396
Life Exp -0.1040171 0.3241050 -0.5553735 1.0000000 -0.7802406 0.5239410
Murder 0.3457401 -0.2174623 0.6723592 -0.7802406 1.0000000 -0.4367330
HS Grad -0.3833649 0.5104809 -0.6545396 0.5239410 -0.4367330 1.0000000
#结论
#收入和高中毕业率之间有很强的正相关
#文盲率和预期寿命之间存在很强的负相关
#偏相关
#控制一个或多个定量变量时,另外两个定量变量之间的相互关系。
#ggm中的pcor()函数用于计算偏相关数
pcor(u,s)
#u是一个数值向量,其那两个值表示要计算的相关系数的变量下标,其余的数值为条件变量的下标。s为变量的协方差阵。
library(ggm)
colnames(states)
pcor(c(1,5,2,3,6),cov(states))
#控制收入、文盲率和高中毕业率,人口和谋杀率之间的相关系数为0.346。
#其他相关
polycor()包的hetcor()函数可以计算一种混合的相关矩阵,其中包含数值型变量的Person积差相关系数、数值变量和有序变量之间的多系列相关系数、有序变量之间的多分格相关系数以及二分变量的四分相关系数。
相关性检验:使用cor.test()函数对单个的Person、Spearman、Kendall相关系数进行检验,简化后的格式为:
cor.test(x,y,alternative,method=)
x,y为要检验的相关性的变量,alternative则用来指定进行双侧检验或单侧检验,而method用以指定要计算的相关模型("person","kendall","spearman")。当研究的假设为总体的相关系数小于0时,要使用alternative="less";在研究的假设为总体的相关系数大于0时,要使用alternative="greater"。在默认情况下,alternative="two.side"
states<-state.x77[,1:6] cor.test(states[,3],states[,5]) #输出结果 data: states[, 3] and states[, 5] t = 6.8479, df = 48, p-value = 1.258e-08 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: 0.5279280 0.8207295 sample estimates: cor 0.7029752
#检验了预期寿命和谋杀率的Pearson相关系数为0的原假设。假设总体的相关度为0,则预计在一千万次中只会右少于一次的机会见到0.703这样打的样本相关度。由于这种情况几乎不可能发生,可以拒绝原来的假设
#对剧中进行显著性检验
library(psych)
corr.test(states,use="complete")
Correlation matrix
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00 0.21 0.11 -0.07 0.34 -0.10
Income 0.21 1.00 -0.44 0.34 -0.23 0.62
Illiteracy 0.11 -0.44 1.00 -0.59 0.70 -0.66
Life Exp -0.07 0.34 -0.59 1.00 -0.78 0.58
Murder 0.34 -0.23 0.70 -0.78 1.00 -0.49
HS Grad -0.10 0.62 -0.66 0.58 -0.49 1.00
Sample Size
[1] 50
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Population Income Illiteracy Life Exp Murder HS Grad
Population 0.00 0.59 1.00 1.0 0.10 1
Income 0.15 0.00 0.01 0.1 0.54 0
Illiteracy 0.46 0.00 0.00 0.0 0.00 0
Life Exp 0.64 0.02 0.00 0.0 0.00 0
Murder 0.01 0.11 0.00 0.0 0.00 0
HS Grad 0.50 0.00 0.00 0.0 0.00 0
人口数量和高中毕业率的相关系数(-0.10)并不显著地不为0(p=0.5)
#其他显著性检验
psych包中的pcor.test()函数可以用来检验在控制一个或多个额外变量时两个变量之间的条件独立性。使用格式为:
pcor.test(r,q,n)
其中r是由pcor()函数计算得到的偏相关系数,q为要控制的变量数,n为样本大小。
4.t检验
研究中最常见的行为就是对两组进行比较。接受某种新药治疗的患者是否较使用某种现有药物的患者表现处了更大的改善?某种工艺是否较另外一种工艺制品的不合格率更少?两种教学手法,哪一种更有效?这里我们将关注结果为连续型的组间比较,并假设其呈正态分布。
#t检验调用格式:
t.test(y~x,data)
其中y是一个数值型变量,x是一个二分变量。调用格式为:
t.test(y1,y2)
其中用y1和y2为数值型向量。可选参数data的取值为一个包含了这些变量的矩阵或数据框
#比较南方group1和非南方group0各州的监禁概率
library(psych)
states<-state.x77[,1:6]
corr.test(states,use="complete")
library(MASS)
t.test(Prob~So,data=UScrime)
Welch Two Sample t-test
data: Prob by So
t = -3.8954, df = 24.925, p-value = 0.0006506
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.03852569 -0.01187439
sample estimates:
mean in group 0 mean in group 1
0.03851265 0.06371269
p<0.001 南方各州和非南方各州监禁的概率不同
非独立样本的t检验
例子:较年轻(14~24)男性的失业率是否和年长的(35~39)男性的失业率更高?在这种情况下,这两组数据并不独立。你不能说亚拉巴州的年轻男性和年长男性的失业率没有关系。在两组的观测之间相关时,你获得的是一个非独立设计。前后测设计或者重复测量设计同样产生非独立的组。
非独立样本的t检验假定组间的差异呈正态分布。调用的格式为:
t.test(y1,y2,paired=TRUE)
其中y1和y2为两个非独立组的数值向量。结果如下:
library(MASS) sapply(UScrime[c("U1","U2")],function(x)(c(mean(x),sd=sd(x))))
with(UScrime,t.test(U1,U2,paried=TRUE)) #输出结果 U1 U2 95.46809 33.97872 sd 18.02878 8.44545
#输出结果
data: U1 and U2
t = 21.174, df = 65.261, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
55.69010 67.28862
sample estimates:
mean of x mean of y
95.46809 33.97872
#差异的均值(61.5)足够大,可以保证拒绝年终和年轻的平均失业率相同的假设。年轻男性的失业率更高一些。
5.组间差异的非参数检验
若两组数据独立,可以使用Wilcoxon秩和检验来评估观测是否是从相同的概率分布中抽得的,调用格式为:
wilcox.test(y~x,data)
wilcox.test(y1,y2)
其中y1和y2为各组的结果变量。可选参数data的取值为一个包含了这些变量的矩阵或者数据框。默认进行一个双侧检验。可以添加参数excat来进行精确检验,指定alternative="less"或alternative="greater"进行方向的检验。
#使用Mann-Whitney U检验监禁率的问题
with(UScrime,by(Prob,So,median))
So: 0
[1] 0.038201
--------------------------------------------------------------------
So: 1
[1] 0.055552
wilcox.test(Prob~So,data=UScrime)
data: Prob by So
W = 81, p-value = 8.488e-05
alternative hypothesis: true location shift is not equal to 0
#p<0.001 说明南方各州和非南方各州监禁率相关的假设不成立
sapply(UScrime[c("U1","U2")],median)
U1 U2
92 34
with(UScrime,wilcox.test(U1,U2,paired=TRUE))
data: U1 and U2
V = 1128, p-value = 2.464e-09
alternative hypothesis: true location shift is not equal to 0
多于两组的比较,如果各组不独立,Friedman检验会更合适。
Kruskal-Wallis检验的调用格式为:
kruskal.test(y~A,data)
其中y是一个数值型结果变量,A是一个拥有两个或更多水平的分组变量。而Friedman检验的调用格式为:
friedman.test(y~A|B,data)
其中A是一个分组变量,而B是一个用以认定匹配观测的区间变量。
以上为基本的统计分析。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号