算法导论day3

算法导论day3

求解分治策略递归式的三种方法

• 代入法
• 递归树
• 主方法

代入法

• 猜测解的形式
• 用数学归纳法求出解中的常数，并证明解是正确的
• 例子
  • 求解T(n)=T(n-1)+n
    
  • 求解T(n)=T(n/2)+1
    

递归树

递归树最适合用来生成好的猜测，然后即可用代入法来验证猜测是否正确。在递归树中，每个结点表示一个单一子问题的代价，子问题对应某次递归函数调用。我们将树中每层中的代价求和，得到每层代价，然后将所有层的代价求和，得到所有层次的递归调用的总代价。
构造递归式\(T(n)=3T(n/4)+cn^2\)的递归树

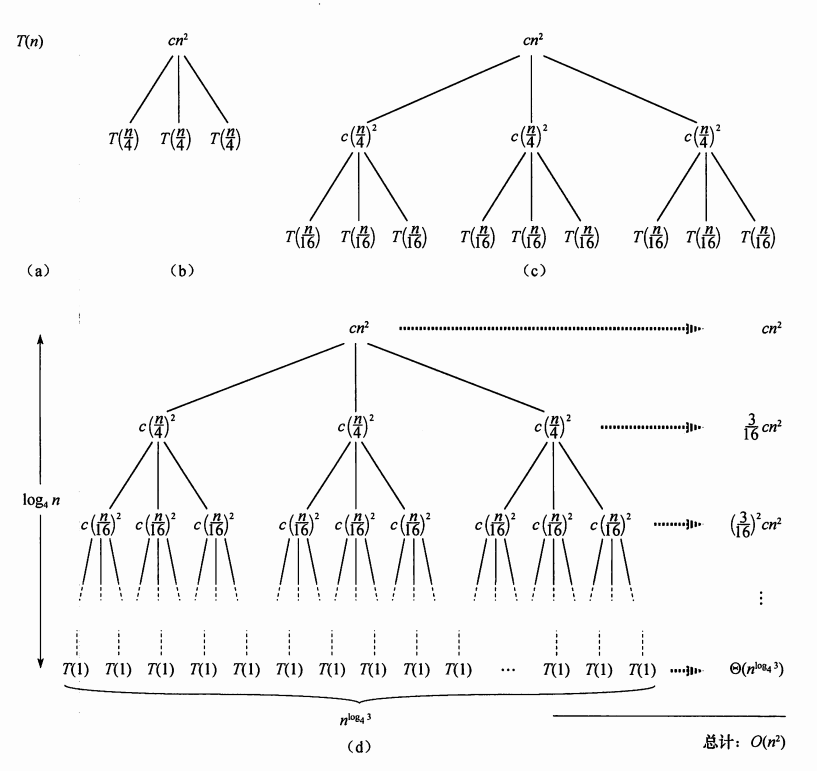
分析： 深度为i的结点对应规模为\(n/4^i\)的子问题。因此当\(n/4^i=1\)，即\(i=\log_4 n\)时，子问题规模变为1。
每层的结点数是上一层的3倍，因此深度为i的结点数为\(3^i\)。因为每一层的子问题规模都是上一层的1/4，所以其对应层的每个结点的代价为\(c(n/4^i)^2\)，所有结点的总代价为\(3^ic(n/4^i)^2=(3/16)^icn^2\)。树的最底层深度为\(log_4 n\)，有\(3^{log_4 n}=n^{log_4 3}\)个结点(求解递归树需要忍受“不精确”)，每个结点代价为T(1)，总代价为\(n^{log_4 3}T(1)\)，即\(\Theta\)

• 例子
  • 求解递归式T(n)=3T(n/2)+n
    
  • 求解递归式\(T(n)=T(n/2)+n^2\)
    

主方法

对于\(T(n)=aT(n/b)+f(n)\)，它描述的是这样一种算法的运行时间：它将规模为n的问题分解成a个子问题，每个子问题规模是n/b，其中a和b都是正常数。a个子问题递归地进行求解，每个花费时间是T(n/b)。函数f(n)包含了问题分解和子问题合并的代价。
主方法主要分析三种情况，如下

对主定理进行直观上分析：即将函数f(n)与函数\(n^{log_b a}\)进行比较。若函数\(n^{log_b a}\)更大，即为上界O，则如情况1；若函数f(n)更大，即为下界\(\Omega\)，则如情况3；若两个函数大小相当,则如情况2，乘上一个对数因子。

• 例子
  • 求解\(T(n)=2T(n/4)+1\)
  • 求解\(T(n)=2T(n/4)+n^{1/2}\)
  • 求解\(T(n)=2T(n/4)+n\)
  • 求解\(T(n)=2T(n/4)+n^2\)
    

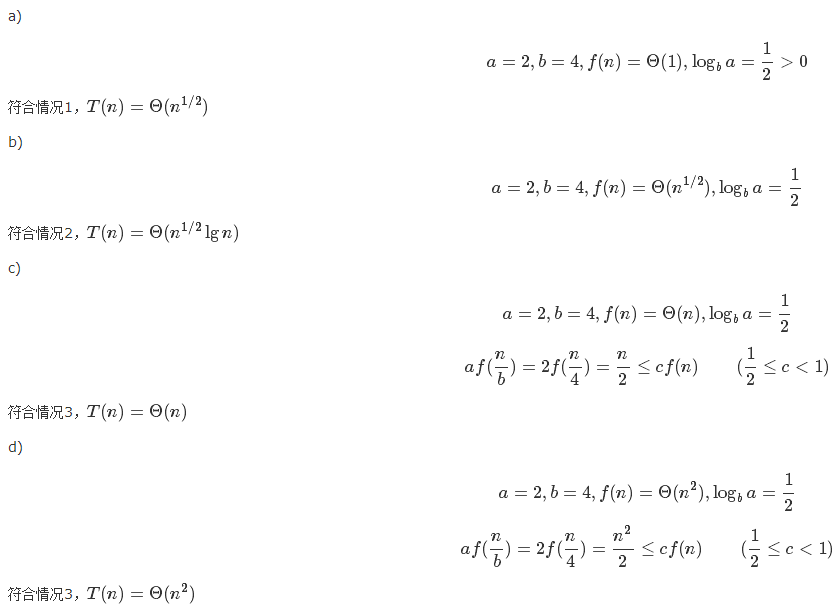
雇佣问题

假设你要雇佣一个新的办公室助理，雇佣代理每天想你推荐一个应聘者(连续推荐n个)，你面试这个人，如果这个应聘者比目前的办公室助理更优秀，你就会辞掉当前的办公室助理，然后聘用这个新的。面试一个人需付给雇佣代理一笔费用，聘用办公助理也需要费用。
假设面试费用为\(C_i\)，雇佣的费用为\(C_h\)，假设整个过程中雇佣了m次，于是总的费用是\(nC_i+mC_h\)。由于n是固定值，总费用的变化取决于m值。

best=0;
for i=1 to n
    interview candidate i;
    if candidate i is better than best
        best=i;
        hire candidate i

生日悖论

一个屋子里人数达到23个人以上，就可以使其他两个人生日是同一天的概率为50%。
证明如下：
首先，假设屋子里有K个人，分别对他们编号1,2,3….k号。不考虑闰年的情况，那么一年就有n=365天，首先还是要假设生日是均匀分布在一年的n天中(喜欢在春天生就都在春天生这就不均匀了)，然后还要假设两个人生日相互独立(什么双胞胎那些还用得着算么)，那么两个人同一天(具体的一天)生日的概率就\(1/n^2\) (生日的概率是1/n,两个人同一天生日当然就相乘了~)，那么两个人同一天生日(365天随便一天)的概率就是1/n (n个\(1/n^2\)相加)
也就是说假如屋里面有两个人，那么他们同一天生日的概率是1/365,那现在要解决的问题是，屋里要有多少人，才能使这个概率上升到1/2 ?
用事件的对立面来求，假设事件P={屋里至少两个人生日一样}，Q={屋里每个人生日都不一样}，那么P=1-Q;
设\(B_k\)为k个人生日互不相同，则\(B_k=B_{k-1}\bigcap A_i\),可得\(P(B_k)=P(B_{k-1})*P(A_k|B_{k-1})=...=P(B_1)*P(A_2|B_1)*P(A_3|B_2)...P(A_k|B_{k-1})=1*(1-1/n)(1-2/n)...(1-(k-1)/n)\)
最后由\(1+x<=e^x\)可得\(P(B_k)<=e^{-k(k-1)/2n}<=1/2\),解得当n=365时，必有k>=23。

球和箱子

这个例子其实就是概率学经常考察的例子，相信学过概率学的应该很熟悉。

在线雇佣问题

不希望面试所有的应聘者以找到最好的一个，也不希望因为有更好的申请者不停地雇佣新人解雇旧人，因为必须遵循每次面试后必须提供职位或者拒绝的要求。因此通过以下方式对该问题进行建模：面试后给出分数Score(i)，选择一个正整数\(k<n\)，面试然后拒绝前k个应聘者，再雇佣其后比前面应聘者有更高分数的第一个应聘者。如果最好的应聘者在前k个面试之中，那么将雇佣第n个应聘者。(个人感觉这个应聘方案有点逻辑不正常，应该没有哪个公司用这么智障的方案吧-_-)

on-line-maximum(k,n){
    bestscore=-1/0;
    for i=1 to k{
        if score(i)>bestscore
            bestscore=score(i);
    }
    for i=k+1 to n{
        if score(i)>bestscore
            return i;
    }
    return n;
}

leetcode

单纯理论实在有点烦躁，所以后面的文章在最后基本会有一题leetcode中的算法题，希望能够坚持并提高自身算法能力。
++Question++
Given a string, find the length of the longest substring without repeating characters.
Examples:
Given "abcabcbb", the answer is "abc", which the length is 3.
Given "bbbbb", the answer is "b", with the length of 1.
Given "pwwkew", the answer is "wke", with the length of 3. Note that the answer must be a substring, "pwke" is a subsequence and not a substring.

---

++问题分析：++ 这道题是为了求出字符串中连续的不存在相同字符的最大子字符串的长度。算法原理为：遍历整个字符串，将满足条件的子字符串长度保存到长度变量中，一旦遍历到相同的字符，则将子字符串的起始位置指向之前的相同字符的下一个字符，继续遍历并将子字符串长度与长度变量比较取较大值。(为什么从下一个字符开始？是因为如果从相同字符之前的字符开始的话，只是从一开始获取的最长字符串中的子字符串，还是会在相同的位置遇到相同的字符)。直至遍历完成，返回最大长度值。

class Solution {
    public int lengthOfLongestSubstring(String s) {
         int res = 0, left = 0, right = 0;
        HashSet<Character> t = new HashSet<Character>();
        while (right < s.length()) {
            if (!t.contains(s.charAt(right))) {
                t.add(s.charAt(right++));
                res = Math.max(res, t.size());
            } else {
                t.remove(s.charAt(left++));
            }
        }
        return res;
    }
}