LeetCode 42. 接雨水

我的LeetCode：https://leetcode-cn.com/u/ituring/

我的LeetCode刷题源码[GitHub]：https://github.com/izhoujie/Algorithmcii

LeetCode 42. 接雨水

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 感谢 Marcos 贡献此图。

示例:

输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路

只要记住水往低处流，所以我们只要关注较低的柱子就行；
想象数组左右两侧都有一个限高柱，然后左右指针分别依次往里推进，每次左右中较低的柱子用来跟于它同侧的限高柱比较，若低于限高柱表示可搜集，否则更新该侧限高柱，同时该侧指针内移，进入下个循环；
另一个思路是直接计算面积差，详细看图解；

思路1-滑动窗口思想

把数组整个看做一个滑动窗口，左右边界有限高柱，左右指针交替内移；

1. 初始化左右边界限高柱为左右边界值；
2. 左右指针交替往内搜集雨水：每次较小的指针跟与其同侧的限高柱对比，小于说明可搜集差值的雨水，否则更新该侧的限高柱为当前指针值，然后指针内移；
3. 重复2逻辑直至左右指针相遇；

总结：滑动窗口/动态规划的核心是找到状态量的转移，或者说是转移方程，本题若f(n)表示数组值，对于左侧限高柱的逻辑则 f(n)=max(f(n),f(n+1))，同时可搜集的雨水为f(n)>f(n+1)?f(n)-f(n+1):0；

思路2-面积差数学直接求解

面积差计算步骤：

1. 从左往右扫描一遍，逐次求最大值累加；
2. 从右向左扫描一遍，逐次求最大值累加和；
3. 减去原来数组的面积和步骤1、2中最大值与数组长度构成的矩形的面积；
   直接看会懵的，看图解配代码就明白了:
   

核心代码：
代码很简单，耐心先看明白代码做了什么，然后看图解；

while (i < len) {
	// 从左向右不断求最大值，向右平铺面积值
	leftMax = Math.max(leftMax, height[i]);
	// 从右向左不断求最大值，向左平铺面积值
	rightMax = Math.max(rightMax, height[j - i]);
	// 顺带减去原数组的面积值
	rst += leftMax + rightMax - height[i++];
}
// 最后减去平铺后最高点与数组长度组成的矩形面积就是雨水面积
return rst - len * leftMax;

代码分解看：

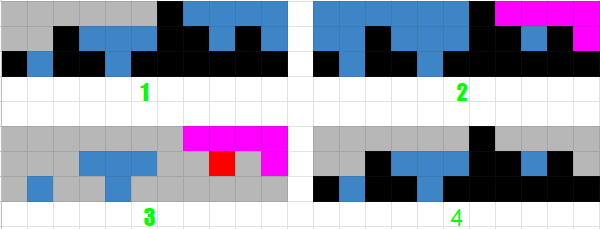
• 先看leftMax = Math.max(leftMax, height[i]);和rst+=leftMax 部分，这里最后累加的就是图1的面积（所有颜色）；
• 再看rightMax = Math.max(rightMax, height[j - i]);和rst+=rightMax 部分，这里最后累加的就是图2的面积（不包括粉色部分）；
• 然后看一下rst+=leftMax - height[i++]部分，这里最后得到的是图3表示的面积（所有颜色）；
• 重点是，我们得到的图3中，如果取出粉色部分加到图2上就会得到一个最大值与数组长度组成的完整矩形，并且图3中红色的部分在图2中重复计算了一次，
  所以实际上rst += leftMax + rightMax - height[i++];这里我们最后拿到的雨水的面积加整个矩形的面积再加红色部分的面积，那么，如果我们减去矩形部分的面积（红色部分只减去了一次）不就得到雨水的面积了么？Bingo!!!
• 所以最后return rst - len * leftMax; 代码这里我们再减去矩形的面积就可以了，即最终图4中淡蓝色部分的雨水面积；

思路3-使用单调栈，本题是单调递减栈

步骤：

1. 从左至右，数组高度递减入栈，遇到非递减的值就开始搜集雨水；
2. 可搜集的雨水是左右两侧挡板的高度较低者减去中间的垫底高度再乘以左右两侧挡板的水平距离差；
3. 一次遍历完，累加2中搜集到的雨水并返回；

图解：图中例子数组数据为[4，3，2，3，2，5，2，1]

算法源码示例

package leetcode;

/**
 * @author ZhouJie
 * @date 2020年2月1日 下午10:44:25 
 * @Description: 42. 接雨水
 *
 */
public class LeetCode_0042 {

}

class Solution_0042 {
	/**
	 * @author ZhouJie
	 * @date 2020年2月1日 下午11:52:28 
	 * @Description: TODO(方法简述) 
	 * @return int 
	 * @UpdateUser-UpdateDate:[ZhouJie]-[2020年2月1日 下午11:52:28]  
	 * @UpdateRemark:1- 
	 *
	 */
	public int trap_1(int[] height) {
		if (height == null) {
			return 0;
		}
		int rst = 0, leftMax = 0, rightMax = 0;
		int i = 0, j = height.length - 1;
		while (i < j) {
			// 若左侧挡板低，则由左侧向内搜集雨水，否则从右侧向内搜集
			if (height[i] < height[j]) {
				if (height[i] < leftMax) {
					rst += leftMax - height[i];
				} else {
					leftMax = height[i];
				}
				i++;
			} else {
				if (height[j] < rightMax) {
					rst += rightMax - height[j];
				} else {
					rightMax = height[j];
				}
				j--;
			}
		}
		return rst;
	}

	/**
	 * @author: ZhouJie
	 * @date: 2020年4月4日 上午2:03:37 
	 * @param: @param height
	 * @param: @return
	 * @return: int
	 * @Description: 2-面积差法，数学方法；
	 *
	 */
	public int trap_2(int[] height) {
		if (height == null) {
			return 0;
		}
		int rst = 0, leftMax = 0, rightMax = 0, len = height.length;
		int i = 0, j = len - 1;
		while (i < len) {
			// 从左向右不断求最大值，向右平铺面积值
			leftMax = Math.max(leftMax, height[i]);
			// 从右向左不断求最大值，向左平铺面积值
			rightMax = Math.max(rightMax, height[j - i]);
			// 顺带减去原数组的面积值
			rst += leftMax + rightMax - height[i++];
		}
		// 最后减去平铺后最高点与数组长度组成的矩形面积就是雨水面积
		return rst - len * leftMax;
	}
	/**
	 * @author: ZhouJie
	 * @date: 2020年4月5日 下午1:45:00 
	 * @param: @param height
	 * @param: @return
	 * @return: int
	 * @Description: 3-单调栈-单调递减栈
	 *
	 */
	public int trap_3(int[] height) {
		if (height == null) {
			return 0;
		}
		Stack<Integer> stack = new Stack<Integer>();
		int allRain = 0;
		for (int i = 0; i < height.length; i++) {
			while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
				int top = stack.pop();
				// 小于栈顶元素就一直入栈
				while (!stack.isEmpty() && height[stack.peek()] == height[top]) {
					stack.pop();
				}
				if (!stack.isEmpty()) {
					// 栈非空时可能搜集到雨水
					// 搜集到的雨水为：左侧height[left]和右侧height[i]两个挡板的较低者减去中间的height[top]底部高度乘以
					// left和i之间的距离(i - left - 1)
					int left = stack.peek();
					allRain += (Math.min(height[left], height[i]) - height[top]) * (i - left - 1);
				}
			}
			stack.push(i);
		}
		return allRain;
	}
}