滑动窗口的极值与deque用法
在程序设计中,为了优化算法可能会用到滑动窗口或者双指针的思想,这种算法能够蛮力情况下的复杂度\(O(n^2)\)降低为线性。滑动窗口的问题通常可以用双指针来解决,即用头尾两个指针来约束窗口大小。
网上对于这两个名词的定义和解释莫衷一是。个人理解,固定一段窗口/区间大小而衍生的问题可以理解为单纯的滑动窗口问题,而双指针思想不局限于解决滑动窗口问题,还包含快慢指针、对撞指针(双指针向内移动)等,本质在于以两个指针来维护问题域,并且能在均摊O(1)下得到可行解。
本文基于Python deque双端队列,以最容易理解的方式归纳滑动窗口的问题的求解方法。
deque双端队列
Python的双端队列类型在官方collections库中,是一种类似原生列表(list)的容器,实现了在队列两端快速添加(append/appendleft)和弹出(pop/popleft)。源码由C语言实现,可在Github的CPython项目下Modules/_collectionsmodule.c文件中找到。
deque本质是一个双向链表,每个节点是一个固定长度的block,可以包含64个元素。在源码注释中,设计者提到固定长度的block可以
1)避免频繁分配内存的开销,提高效率;
2)大幅减少了链表指针,提升数据/指针比,从而提升内存利用率;
3)有利于缓存局部性。
点击查看源代码
/* The block length may be set to any number over 1. Larger numbers
* reduce the number of calls to the memory allocator, give faster
* indexing and rotation, and reduce the link to data overhead ratio.
* Making the block length a power of two speeds-up the modulo
* and division calculations in deque_item() and deque_ass_item().
*/
#define BLOCKLEN 64
#define CENTER ((BLOCKLEN - 1) / 2)
#define MAXFREEBLOCKS 16
/* Data for deque objects is stored in a doubly-linked list of fixed
* length blocks. This assures that appends or pops never move any
* other data elements besides the one being appended or popped.
*
* Another advantage is that it completely avoids use of realloc(),
* resulting in more predictable performance.
*
* Textbook implementations of doubly-linked lists store one datum
* per link, but that gives them a 200% memory overhead (a prev and
* next link for each datum) and it costs one malloc() call per data
* element. By using fixed-length blocks, the link to data ratio is
* significantly improved and there are proportionally fewer calls
* to malloc() and free(). The data blocks of consecutive pointers
* also improve cache locality.
deque支持的方法与list类似,由于可以从队首(以下将列表左端看作队首)插入和删除,因此增加了 appendleft 和 popleft 方法。
deque支持下标访问,没有提供 size 或 length等方法,可以用 len 函数来获取队列元素个数。队列常用操作方式总结如下表。
| 操作 | 代码 |
|---|---|
| 创建队列 | from collections import queue q = deque() |
| 队列长度 | len(q) |
| 获取队首 获取队尾 |
q[0] q[-1] |
| 插入队尾 插入队首 |
q.append(item) q.appendleft(item) |
| 删除队尾 删除队首 |
q.pop() q.popleft() |
滑动窗口问题
滑动窗口的均值
这是一个比较基本的,不需要用特殊数据结构的问题。在滑动过程中,我们需要维护窗口的总和。对于每一次移动,只需要加入新进来的右端元素并减去移出的最左端元素,就能得到新的总和。将总和除以窗口长度即为窗口内所有元素的均值。
滑动窗口的最大值
如何维护一段窗口的最大值?一种想法是,可以用大顶堆。我们在大顶堆中同时存放元素和下标,我们总能在 O(1) 时间内获得最大值;当堆顶元素过期时,最多删除n-k次。移动过程中,不断将新的元素加入堆中。由于删除和增加都不超过 n 次,每次调整的操作均为O(logn),因此总复杂度为 O(nlogn)。
上述实现中的堆维护了冗余的数据,比如窗口大小为 k,但堆的大小可能很大,除堆顶外,堆中很多元素可能已经不在窗口中,但没有及时删除。
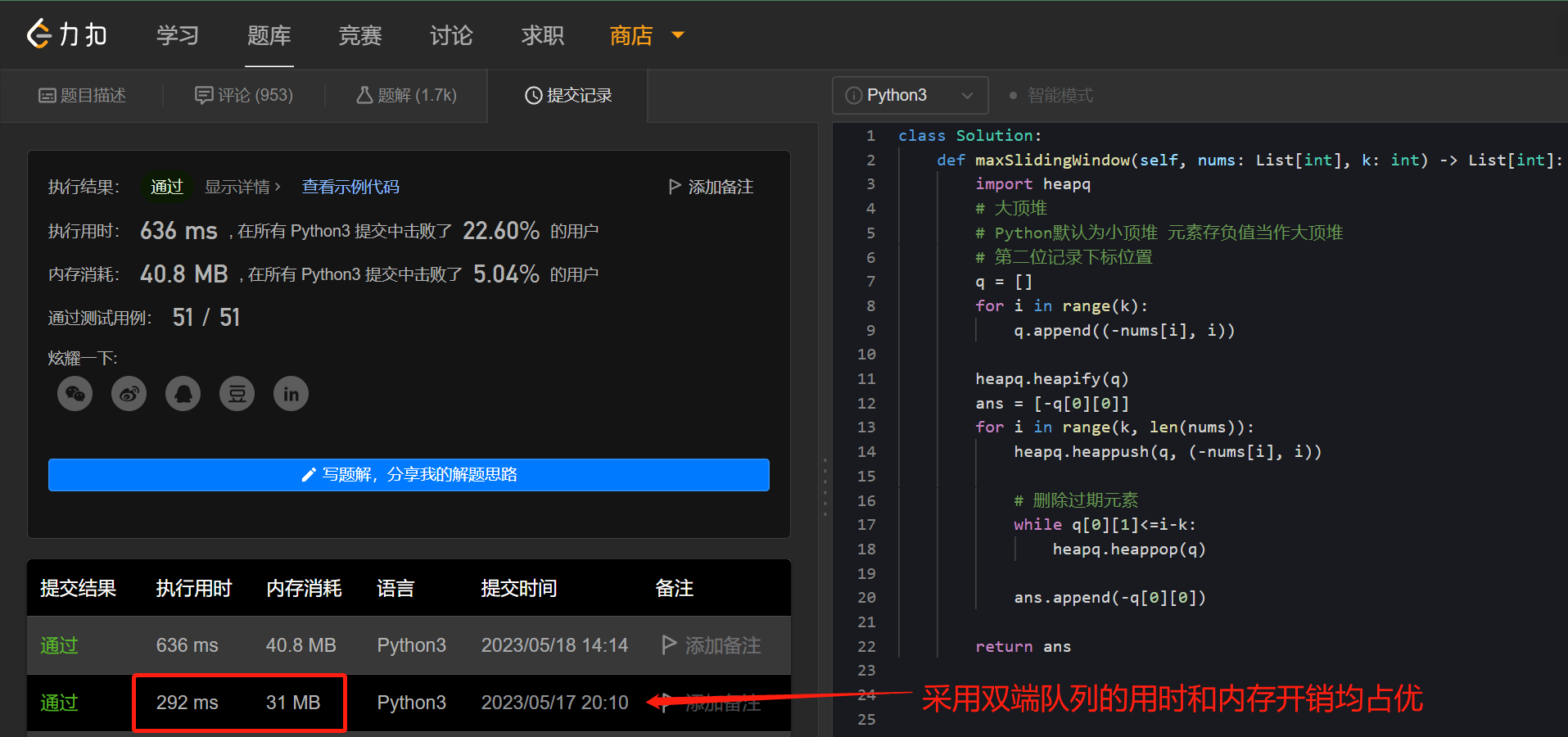
改进思路是维护一段单调队列,队列中的元素按升序排列,队尾元素是最大值。
每次移动,我们需要:
- 维护队尾的最大值是否过期(窗口大小为k)
- 将队首开始,所有不大于插入值的元素删除,然后放入队首(维护单调性)
其中 1. 保证了每次O(1)获取历史窗口内的最大值; 2. 由于只关心最大值,在窗口中先进来的、且比插入元素更小值永远不会作为滑动过程中的答案,因此可以直接删除。
滑动过程中,队列中元素个数不超过 k,每个元素最多一次入队,一次出队,因此算法的复杂度为 O(n)。
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
# 双端队列 窗口长度为k 按升序排列下标
q = deque()
# 先放k个值入队列
for i in range(k):
# 把队首小的pop掉 滑动过程中总会先出去
while q and nums[q[0]]<=nums[i]:
q.popleft()
# 最大元素在队尾 q[-1] or q.pop()
q.appendleft(i)
ans = [nums[q[-1]]]
for i in range(k, len(nums)):
# 我们的最大值在队尾
# 因此只用检查队尾是否过期
# 窗口区间 [i-k+1.. i] 长度为 k
# 窗口内下标至少为 i-k+1
while q and q[-1]<=i-k:
q.pop()
# 插入新的元素 与上面相同
while q and nums[q[0]]<=nums[i]:
q.popleft()
q.appendleft(i)
# 记录答案
ans.append(nums[q[-1]])
return ans


 浙公网安备 33010602011771号
浙公网安备 33010602011771号