矩阵分析与应用笔记 | 国科大李保滨课程总结
1 课程介绍
2-3 线性方程组
高斯消去法
交换两行,任意行数乘,一行数乘加到另一行
==> 上三角形
==> 回代
复杂度
乘法
加法
Gauss-Jordan法
多了两个步骤
- pivot变为1
- 消去pivot上面的元素
变换为单位阵
复杂度
乘法
加法
部分主元法
交换行使主元最大(绝对值)
行阶梯形 定义了矩阵的秩
修改高斯消去法
每行从左到右找非零元,消去后不一定得到上三角形式
秩
- 主元pivot的数量
- 非零行的数量
- 基本列(包含主元)的数量
齐次方程
非齐次方程
右边含有非零数值
平凡解
x=0
[A|b] ==> E[A|b]
解的形式
x = p非齐次方程特解 + (n-r)齐次方程通解
4 矩阵代数
矩阵加法性质
标量乘法性质
共轭转置
对称性
矩阵乘法
不可交换
乘积的行列
分配律 结合律
转置
分块乘法
逆矩阵
逆存在性等价描述
- rank(A) = n
- Gauss-Jordan, A –> I
- Ax = 0 ==> x =0
逆的计算
复杂度
三种基本行变换
交换两行
乘上a倍
第一行a倍加到第三行
左乘:基本行变换
相似矩阵
秩相等
推论:与非奇异矩阵的乘法不改变秩
LU分解
A = LU
解方程
LUx = b
Ux = y, Ly = b
5 向量空间
定义 两个集合 两个基本运算:加法和标量乘法
(1)加法封闭
(2)加法结合律
(3)加法交换律
(4)加法零元
(5)加法逆元
(6)数乘封闭
(7)数乘结合律
(8)数乘分配律
(9)数乘分配律
(10)单位元
子空间
是V的子集且满足
(1)加法封闭
(6)数乘封闭
张成集合
,
子空间
Range Spaces值域空间
列空间
R(A),相当于,也叫 A 的像空间(image space)
行空间,左值域
Nullspace 零空间
-
-
左零空间
线性无关
A 的列构成线性无关集合
等价于
-
rank(A)=n
-
N(A) =
对角占优矩阵是非奇异的
Vandermonde Matrices
Wronski matrix
basis 基
A linearly independent spanning set for a vector space V is called a basis of V.
一组线性无关的张成集合
标准基
空间:
多项式:{1, x, x^2, … x^n}
{0}:空集
等价命题
- 最小的张成集合
- 最大线性无关子集
维度
等价命题
-
V 基的向量个数
-
V 最小张成集合的向量个数
-
V 最大线性无关子集的向量个数
秩

等价命题
rank(A)
- 等价A的行阶梯矩阵的非零行
- 行阶梯矩阵主元数量
- 基本列数量
- 线性无关列数量
- 线性无关行数量
- dim R(A)
- dim R(A^T)
- n - dim N(A)
- m - dim N(A^T)
- A中最大非奇异矩阵
incidence matrix 入射矩阵
包含 m 个节点 n 条边
每条边对应一列中,一列中包含一组 1, -1 ,对应出点和入点
连通图,rank(E) = m - 1
Normal Equations
Rank等价定义

6 线性变换
零变换
恒等变换
线性变换
从
线性算子
旋转 Q
投影 P
反射 R
有限维空间的线性变换都有矩阵表示
空间的向量u 在基 下表示为
称为 关于B的坐标
线性变换空间
表示所有从U变换到V的集合
, 其中
-
基
-
dim L(U,V) = (dim U) (dim V)
坐标矩阵表示
每个 u 在 B’ 下的坐标表示作为每一列

坐标变换转化为矩阵乘法
,其中 为 u 经过 T 变换后在 v 下的坐标表示。
代表 ,为方阵
基变换

坐标变换

相似性
:存在非奇异矩阵Q,使得 。
相似变换: , 。
不变子空间
定义
-
在变换T下的不变子空间 , 且
-
T 这时可以作为一个线性算子,表示为 。
上三角和对角块形式
T 是 n x n矩阵,下面的命题是等价的
- 当且仅当 Q 的前 r 列张成 T 下的不变子空间
- 当且仅当 Q = (Q1|Q2|…|Qk),每一个 Qi 张成 T 下的不变子空间
7-8 模和内积
Norms模--长度
模:空间几何的概念
范数:线性代数中的概念
向量的模满足
- 正定性 当且仅当 x=0,
- 齐次性
- 三角不等式
欧几里得模
复数向量
p-模
矩阵的模满足
- 正定性
- 齐次性
- 三角不等式
- 相容性
Frobenius矩阵模
矩阵2模
,其中 为 的最大的特征值。
矩阵1模、无穷模
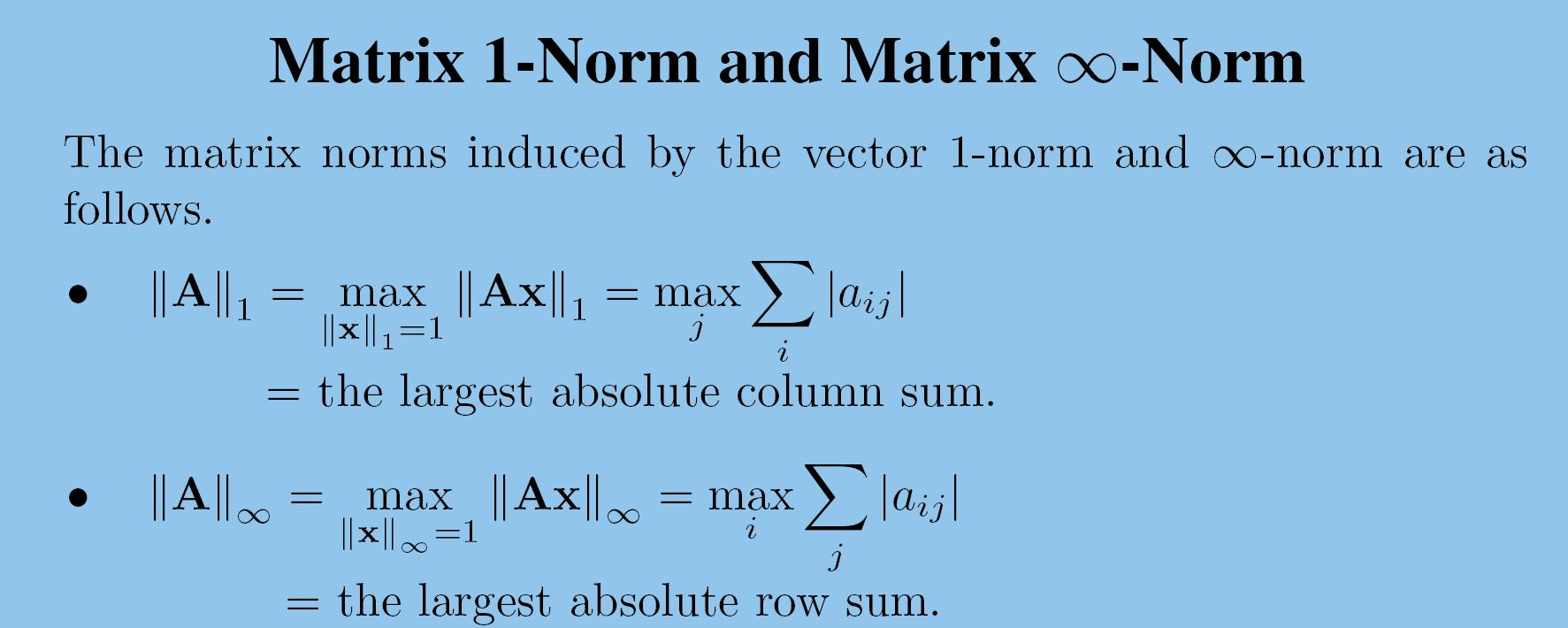
Inner Products内积--夹角/几何关系
内积
标准向量内积
椭圆内积
标准矩阵内积
内积空间可以定义模:
模等于内积开方
满足平行四边形法则,才有:
内积等于模平方
只有在 p=2情况下 平行四边形法则才满足,因此内积只能产生欧几里得模(二模)
因为左边p-模等于2* 2^(2/p),右边p-模恒等于4
正交
正交
角度
标准正交集合/规范正交基
GramSchmidt施密特正交化

QR分解
把A写成n列,进行施密特正交化分解
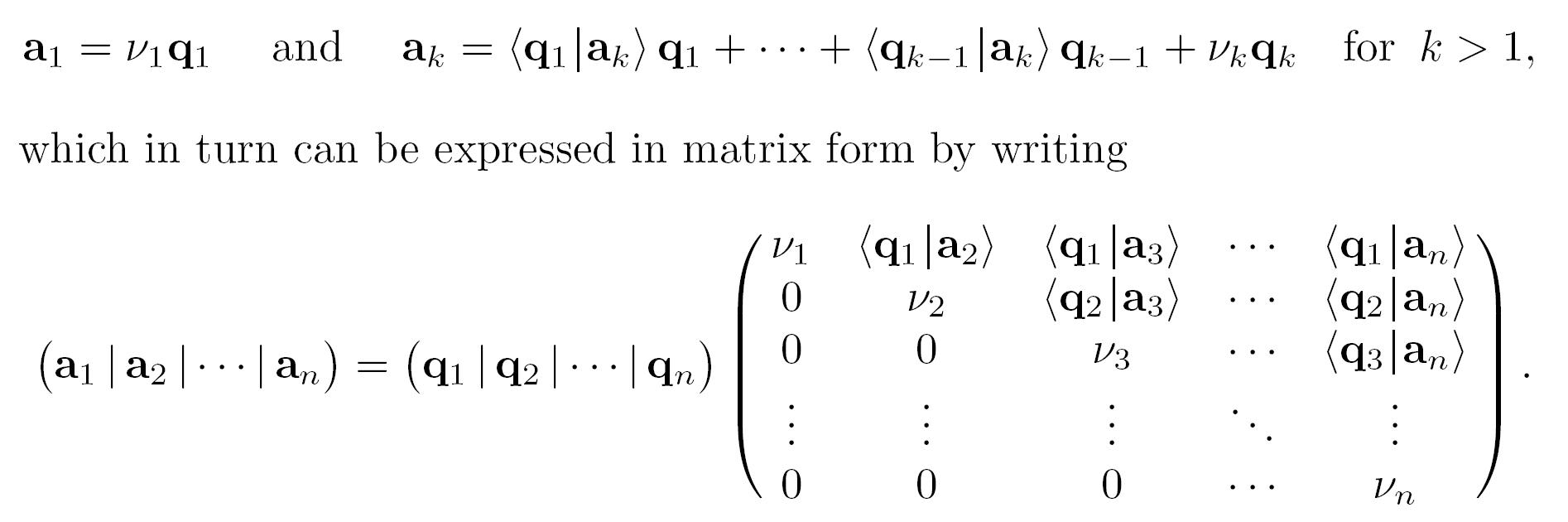
将A分解为 Q R
如果 是非奇异矩阵,Q是单位正交基,所以 。
改进的施密特正交化
正交矩阵
酉矩阵和正交矩阵
Unitary and Orthogonal Matrices
酉矩阵(正交矩阵) 列构成标准正交基(复数域、实数域)
与酉矩阵相乘,不改变向量的长度
等价命题
- 行 标准正交
- 列 标准正交
- 逆等于转置
- 不改变向量长度
单位矩阵(identity matrix) I是正交矩阵
置换矩阵是正交矩阵
初等正交投影算子
投影到u垂直上,其中
正交投影算子
投影到span{u}上
投影到u垂直上
初等镜面反射算子/Householder变换
性质
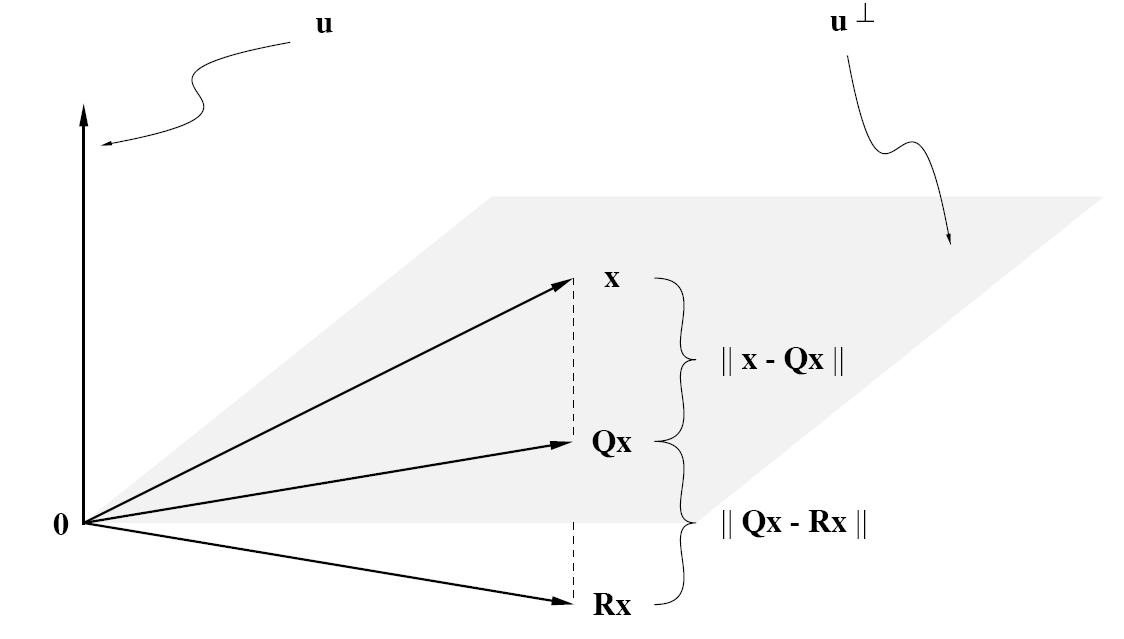
Householder reduction
首先用第一列构造镜面反射算子:
, ,其中
使得
平面旋转/Givens旋转
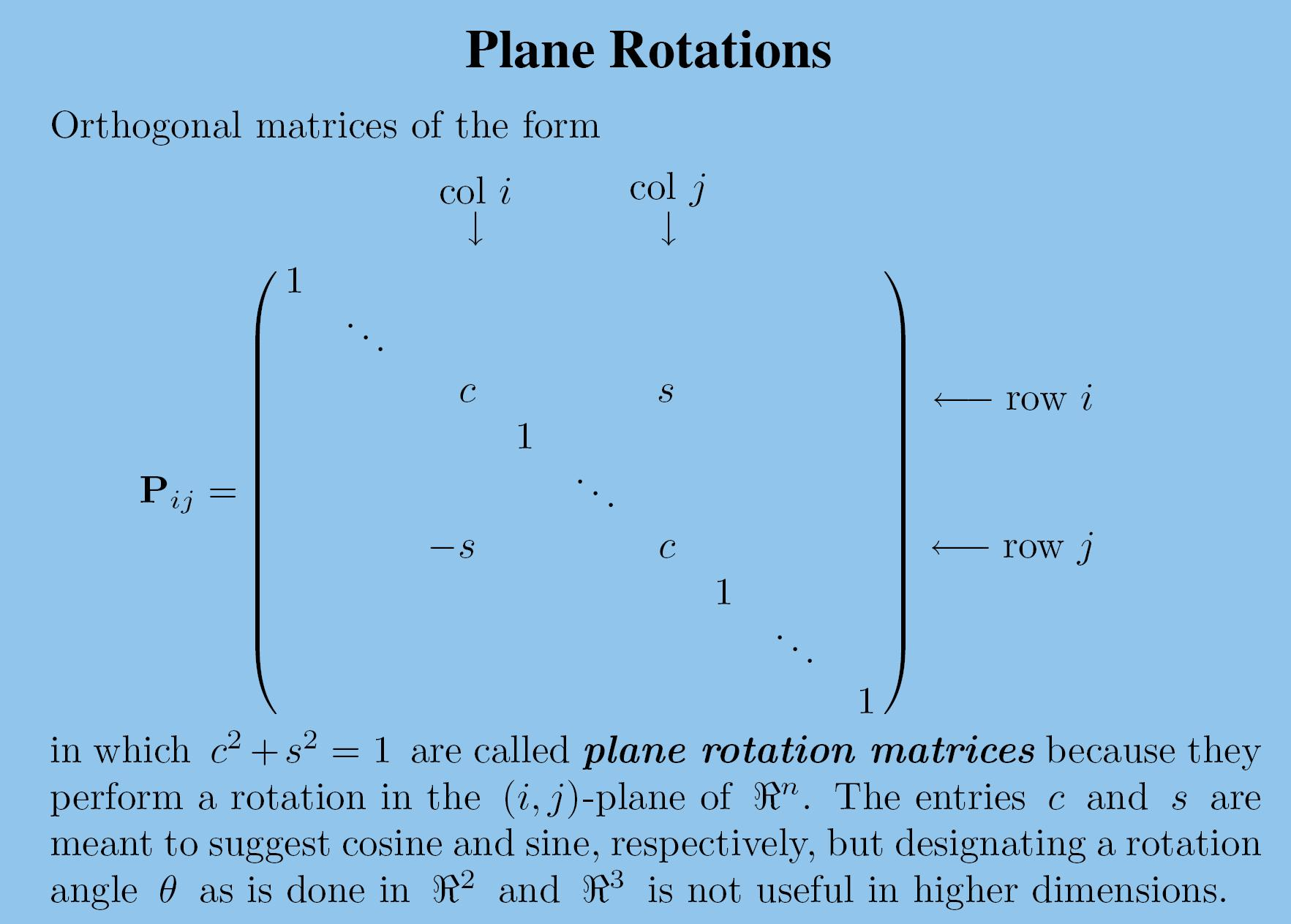
通过旋转,使 的坐标值为0

任意向量,旋转到第 i 个坐标轴上,得到 , 其中
互补子空间 Complementary Subspace
互补子空间
并且
直和
等价命题
- 任意v,有唯一x, y 使得 v = x + y
- 并且 是 V 的基
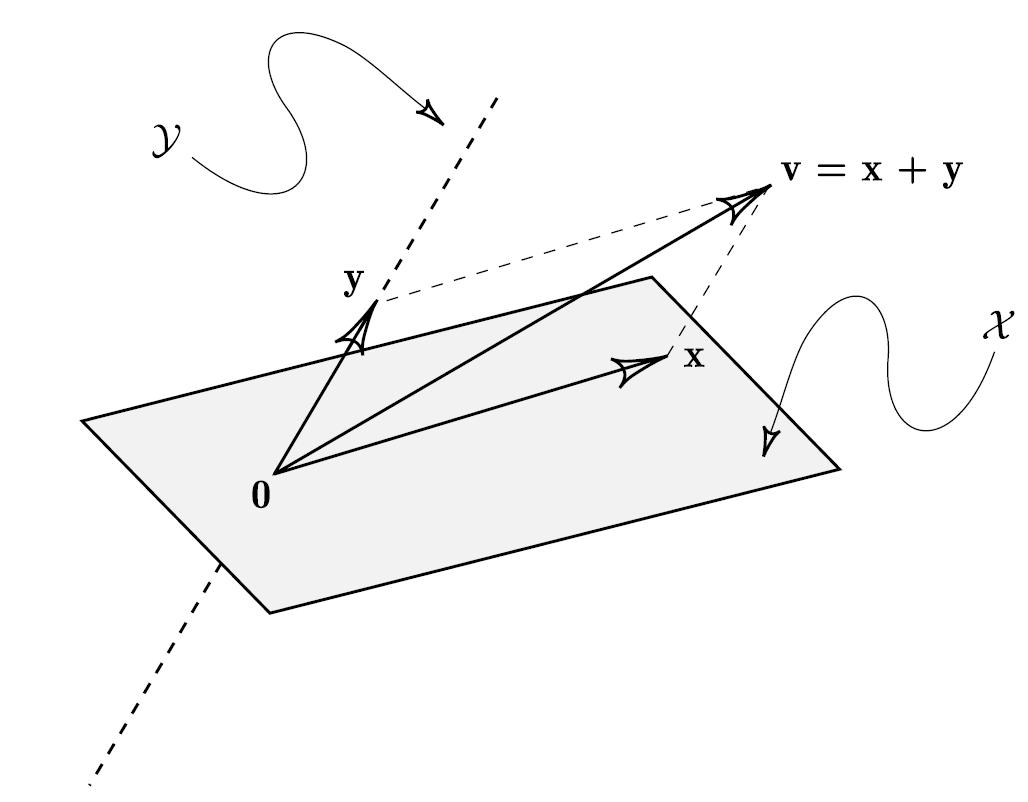
投影
如果 , v = x + y
x 被称为 v 沿 Y 到 X 上的投影
y 被称为 v 沿 X 到 Y 上的投影
投影算子
Pv = x
性质
-
P^2 = P
-
I - P 是互补投影算子(投影到Y)
-
R(P)=N(I-P)=X R(I_P)=N(P)=Y
-
,其中 X, Y 分别为 的基。
满足幂等性质的线性算子就是投影算子 P^2 = P
值零分解Range-Nullspace Decomposition –方阵
值零分解
若A是奇异的,则存在k,使得
,其中 最小的 k 为 A 的 index
若A是非奇异的, 定义index(A)=0
求index
计算 A^k, A^{k+1} 秩不变
幂零矩阵 N^k = 0
核零分解 Core-Nillpotent分解
通过相似变换
,其中 rank(A^k) = r , N^k = 0
Drazin Inverse
方阵
, 其中 k = index(A)
正交分解
正交补
与 W 正交的所有向量的集合
正交补子空间
M 是 V 的子空间,则
若 并且
那么
垂直运算
正交分解理论
对于任意矩阵 A,都有:
矩阵的四个基本子空间
- R(A) 是行空间 的正交补
- N(A) 是行空间 的正交补

URV分解 – 非方阵
数值计算稳定
每个 都有 正交矩阵U, V 和非奇异矩阵 C
- U 的前 r 列是 R(A) 的标准正交基
- U 的后 m-r 列是 R(A)垂直/N(A^T) 的标准正交基
- V 的前 r 列是 N(A)垂直/R(A^T) 的标准正交基
- V 的后 n-r 列是 N(A) 的标准正交基
RPN矩阵 Range Perpendicular to Nullspace
也叫 值域对称矩阵,EP矩阵
非奇异矩阵是平凡 RPN矩阵,零空间是 0
正规矩阵 AA* = A*A
Hermitian A=A*
对称矩阵 A = A^T
等价命题 R(A) = R(A^T)
奇异值分解
每个 都有 正交矩阵U, V 和对角矩阵
应用
- 对单位球变换的拉伸度量
- 线性系统敏感性分析
- 最近的 rank(k)矩阵距离
- 整理嘈杂的数据,提取相关信息,相当于傅里叶展开
伪逆(非方阵)

满足四条 Penrose方程
AA†A = A, A†AA† = A†, (AA†)T = AA†, (A†A)T = A†A
正交投影
每对互补子空间定义了一个投影算子
当子空间互相垂直,则为正交投影
定义
v = m + n, 并且
- m 被称为 v 到 M 上的正交投影
- 沿着 到 M 上的投影算子
构造投影算子
M 是 的基,则
- ,
M 包含标准正交基
正交投影算子
投影算子P 是正交投影算子
等价命题
最近点理论
M 是 内积空间 V 的子空间, b 是 V 的向量,M 上离 b 最近的向量是
p = PMb, b 到 M 上的正交投影
b 和 M 的正交距离:
最小平方解
等价命题
9 矩阵行列式
定义
,其中
行列式表示也可以用
行操作对行列式的影响
两行交换:det(B) = - det(A)
某行数乘:det(B) = a det(A)
i 行 a 倍加到 j 行:det(B) = det(A)
可逆性与行列式
- 非奇异 <==> det(A) /= 0
- 奇异 <==> det(A) = 0
乘积法则
det(AB) = det(A)3det(B) 所有n x n矩阵
A,D为方阵
行列式计算
PA = LU
, 根据行交换次数奇偶性确定
行列式微分
的元素是 t 的可微函数
,其中 表示 A 的第 i 行被该行的微分替代。
秩1矩阵更新
克莱姆法则
,其中 表示 A 的第 i 列替换为 b
代数余子式
求逆
adjugate 伴随矩阵 adj(A) = 代数余子式构成的矩阵的转置
adjoint 伴随矩阵
10 特征值
定义
,其中 和 x 被称为特征值和特征向量
特征值集合, A的频谱spectrum
特征方程

A的行列式 为 特征值之积
A的迹 为 特征值之和
谱半径
A 的最大特征值的绝对值
相似变换对角化
相似性
则A 与 B 相似,左边为A的相似变换
可对角化
A 相似于对角阵 <=> A 有 n 个特征向量 <=> ,P每一列为特征向量
代数重数
特征方程的指数
几何重数
对于每个特征值,代数重数等于几何重数,等价于 A 可对角化
频谱分解

)
正规矩阵
<==> A 可酉对角化,被称为正规矩阵
性质
-
A 是 RPN矩阵
-
R(A − λiI)⊥N(A − λiI).
对称矩阵和Hermitian矩阵
A 是 实对称矩阵 <==> A 正交相似于 实对角矩阵
正定矩阵
等价定义
-
-
对称矩阵A的特征值是正数
-
能分解为非奇异矩阵
-
LU分解后,主元为正
-
顺序主子式为正
-
主子式为正
二次型



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· TypeScript + Deepseek 打造卜卦网站:技术与玄学的结合
· 阿里巴巴 QwQ-32B真的超越了 DeepSeek R-1吗?
· 【译】Visual Studio 中新的强大生产力特性
· 10年+ .NET Coder 心语 ── 封装的思维:从隐藏、稳定开始理解其本质意义
· 【设计模式】告别冗长if-else语句:使用策略模式优化代码结构