Leetcode 90. 子集 II

对于包含 \(n\) 个元素的集合（其中每个元素互不相同），我们容易得到其子集数量为 \(2^n\)。由下面的DFS搜索树可以看到，依次判断每个元素是否加入到当前子集中，直到递归到叶子节点则得到全部 \(2^n\) 个子集。

本问题将输入由集合扩展为可能保护重复元素的数组，仍然求解其所有子集。比较naive的方法是同样先得到全部 \(2^n\) 个子集再去重，但这会增加额外的比较时间和内存消耗。

DFS+剪枝

分析搜索树，我们可以发现，子集重复情况出现在：当连续相同元素在一个分支上，前一次没有选择，而后一次继续选择该元素时发生。例如 输入 nums = [1, 1]， 则搜索树的第三个分支应该剪掉。

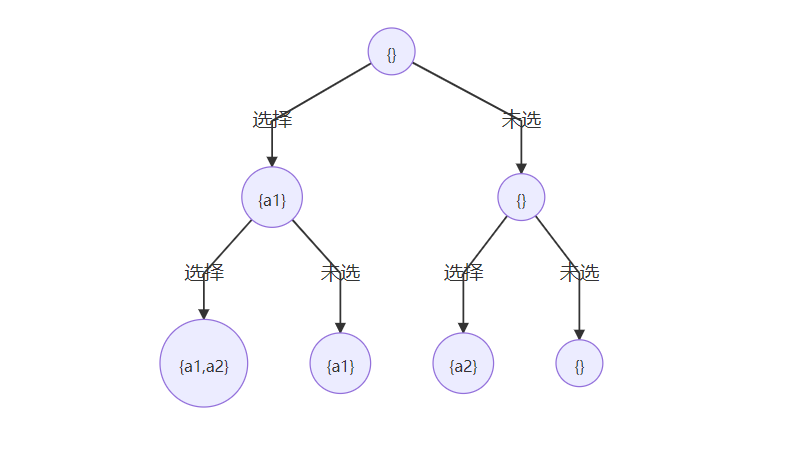
具体代码实现，需要先对输入排序，新加入元素时，进行重复检查进行剪枝。

pos>0 and nums[pos-1]==nums[pos] and not lastChoosed

由于我脑抽，一开始对上次选择 直接使用 not last==nums[pos-1] 进行判断 debug 好久都没AC，因为这样对于连续 3 个相同元素，当搜索到第三个元素时，无法区分第二个元素未选的情况，这样会得到 {1, 1, x}, {1, x, 1} 两组重复答案。
正确的写法如下：

def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
    nums.sort()
    n = len(nums)
    ans = []

    def dfs(pos, cand, lastChoosed):
        if pos==n:
            ans.append(cand)
        return

        if not (pos>0 and nums[pos-1]==nums[pos] and not lastChoosed):
            dfs(pos+1, cand+[nums[pos]], nums[pos])

        dfs(pos+1, cand, False)

    dfs(0, [], False)
    return ans

另一种思路

查看题解，还有另一种解法。

将搜索过程中的状态看作一个子集，我们不断将未选择的元素加入到已选的状态中。那么对于同一层的分支，相同元素的搜索分支应该被剪掉（相当于前面解法前一次未选，后一次仍然选择该元素，这种情况等价于先选择该元素之后不选，而这个分支已经搜索过）。而不同层次则可以重复选择相同元素。

引用Leetcode上的图片说明：

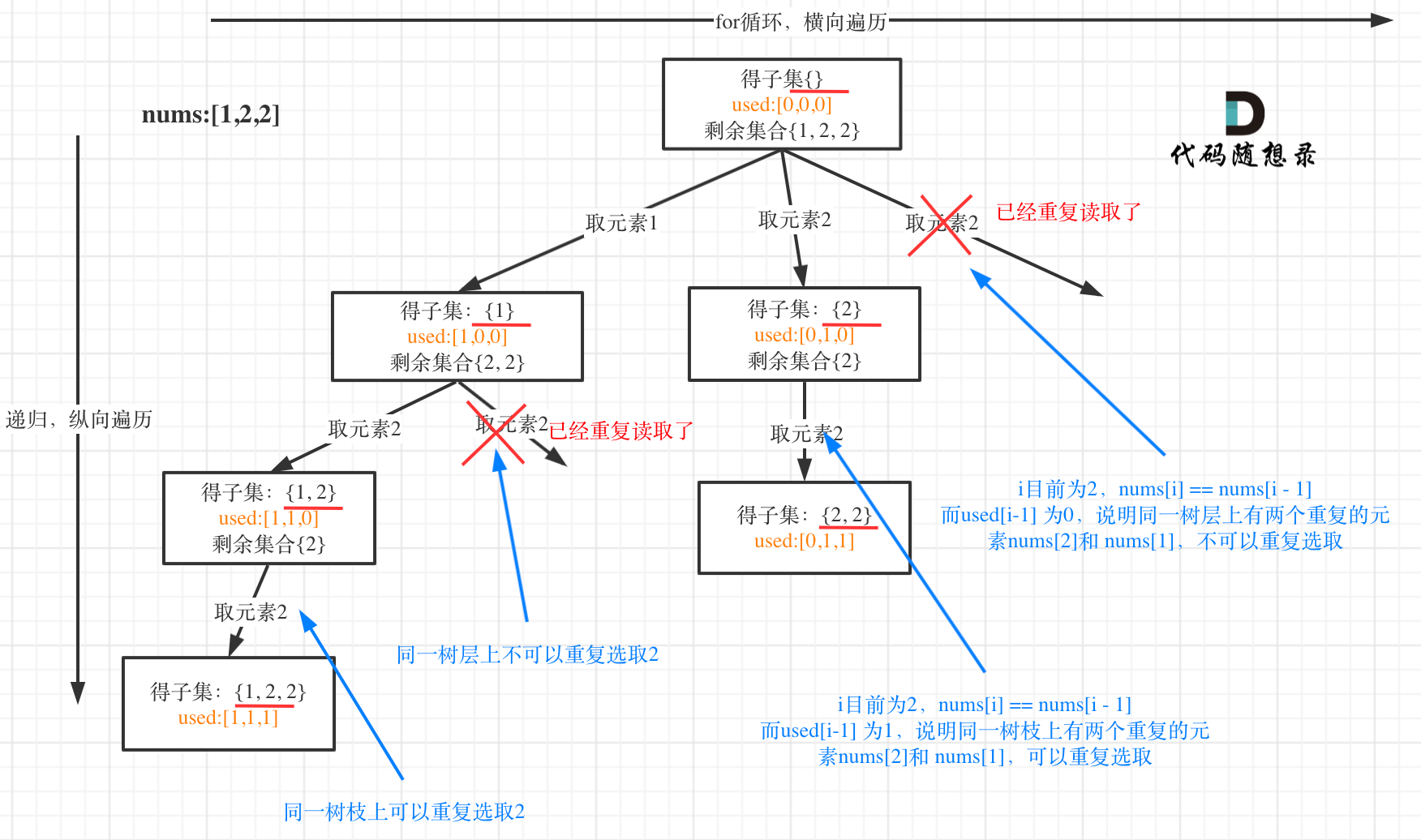
题解代码还能进一步精简：对于 pos 以前的元素为已选的，每次只用选择相邻不同的元素加入候选集中

def dfs(pos, cand):
	ans.append(cand)
    if pos==n:
    	return

	for k in range(pos, n):
		if k==pos or nums[k]!=nums[k-1]:
			dfs(k+1, cand+[nums[k]])

dfs(0, [])

---（完）---