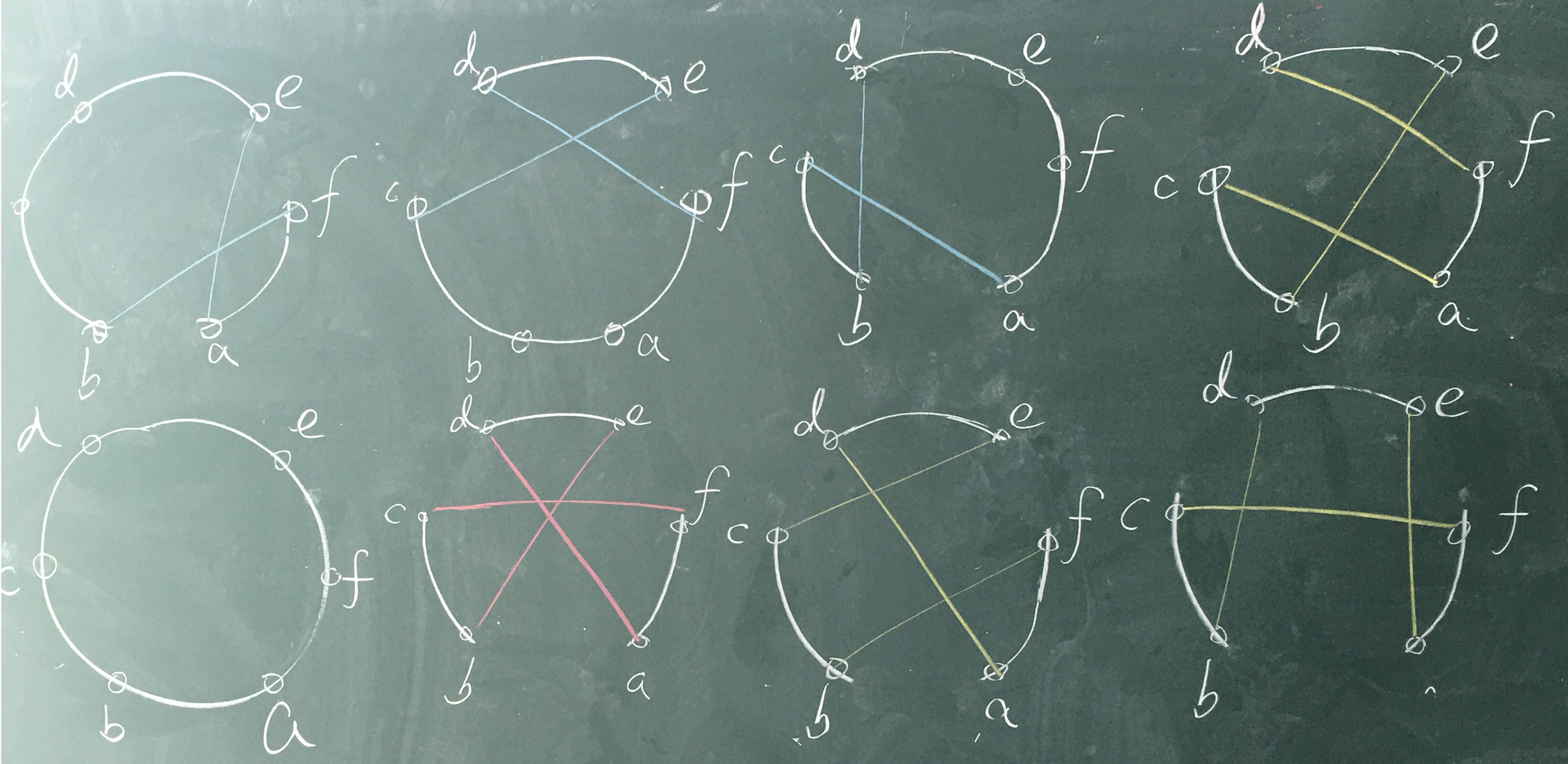算法设计与分析笔记 by 国科大卜东波

Lecture 1 2021.9.10 授课内容

Algorithm 算法一词起源于 学者 Musa al-Khwarizmi（阿尔·花剌子米）。花剌子米是代数学之父，是代数和算术的创立人。算法（Algorism、Algorithm）出自「Algoritmi」，这是花剌子米(al-Khwārizmī)的拉丁文译名。

 

基本算法策略

求解问题一般可以分为三种情况

1. 分治（Divide&Conquer）：根据问题结构划分为子问题，根据问题性质，可能能进一步优化为动态规划（DP）、贪心算法
2. 改进（Improvement）：根据问题解的关系，从一个初始解不断改进
3. 枚举（Enumeration）：根据问题解的形式，使用搜索树枚举每一种解，可能用到剪枝

 

旅行商问题(TSP)

接触过图论的同学应该都熟悉TSP问题，即求解一条通过图 \(G(V, E, w)\) 上每一个节点刚好一次的最短回路。

应用上面的问题求解策略，我们分别使用三种方式来解决该问题。

 

分治

原问题：对于 \(n\) 个城市，访问每个城市刚好一次的回路。

显然，原问题无法被直接划分为两个更小的子问题，因为两个部分的城市回路无法直接合并。这里可以定义子问题为一条最短的路径：\(M(s, S, x)\) 表示从s出发访问城市集合S里每一个城市一次最后抵达x的最短路径的解。

因此原问题等价于求解

\[min_{e \in V, e \neq s} M(s, V-\{e\}, e) + d_{es} \]

M(s, S, x)也很容易划分为更小的子问题

# Held-Karp algorithm [1962]
function TSP(D)
  return mine∈V,e̸=s M(s, V − {e}, e) + des;
function M(s, S, x)
  if S = {v} then
    M(s, S, x) = dsv + dvx;
    return M(s, S, x);
  end if
  return mini∈S, i̸=xM(s, S − {i}, i) + dxi;

 

提升

提升策略关注问题解之间的关系。可以设计以下通用的提升算法流程：

# Improvement strategy
function GenericImprovement(V, D)
# Let s be an initial tour;
while TRUE do
  Select a new tour s′ from the neighbourhood of s;
  if s′ is shorter than s then
    s = s′;
    end if
  if stopping(s) then
    return s;
  end if
end while

 
如果我们已经找到任意一条便利每一个城市的回路，如何改进使回路总距离缩短呢？现在问题转化为上述neighbourhood的定义。

2-OPT：对于一条回路，可以选择两条边上（只改变一条边是不可能的）的四个端点，交换其中两个端点连边，从而形成一条新的回路。

2-OPT可以扩展为3-OPT，这样新的转化方案总共有7种

 

枚举

我们对图上的边编号，对于每一种方案，可以记录每一条边的使用情况，因此解可以表示为类似 X = [0,1,1,... 0,1]的形式，其中 \(X[i]= 1\) 表示通过第 \(i\) 条边， \(0\) 表示不通过。

• 暴力搜索

• 启发式搜索

  lower_bound: 剩余每个节点最短两条边之和

  best_so_far: 当前已经找到的最短路径

  如果当前路径长度已经大于 lower_bound 或 best_so_far，则停止扩展当前部分解

 
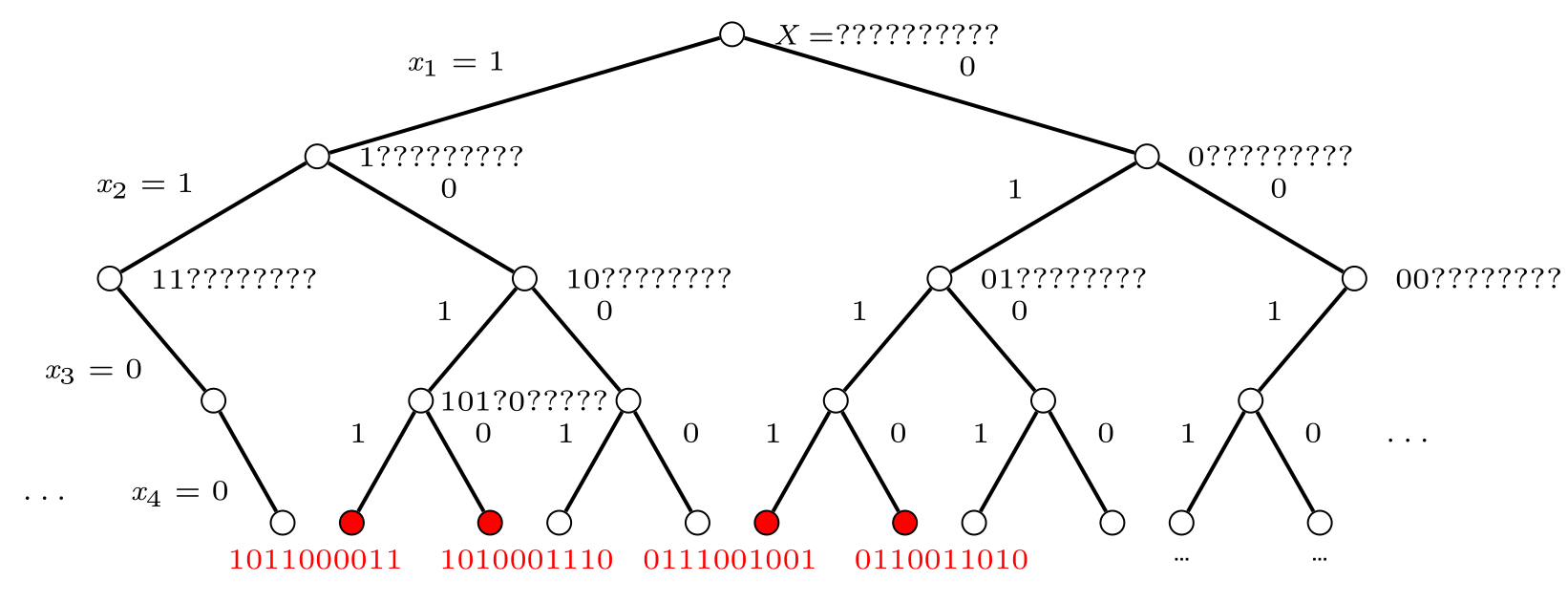
对图上的节点编号，解可以表示为 X = [x1, x2, ... xn-1, xn=x1]。同样可以应用以上的搜索策略。