[算法]字典树

Trie树就是字典树，其核心思想就是空间换时间。

 后缀树 suffix tree:http://www.cnblogs.com/snowberg/archive/2011/10/21/2468588.html

字典树作用：

1、查找单词是否出现

2、查找单词第一次出现位置（在最后一个字母节点标记第一次出现位置）

3、查找包含前序的单词个数（每新增一个单词进树，所经过的节点的计数器加一）

4、将所有单词按字母次序输出

举个简单的例子。

给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，第一次出现第几个位置。
这题当然可以用hash来，但是我要介绍的是trie树。在某些方面它的用途更大。比如说对于某一个单词，我要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单。
现在回到例子中，如果我们用最傻的方法，对于每一个单词，我们都要去查找它前面的单词中是否有它。那么这个算法的复杂度就是O(n^2)。显然对于100000的范围难以接受。现在我们换个思路想。假设我要查询的单词是abcd，那么在他前面的单词中，以b，c，d，f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的，在以a开头中的单词中，我们只要考虑以b作为第二个字母的……这样一个树的模型就渐渐清晰了……
假设有b，abc，abd，bcd，abcd，efg，hii这6个单词，我们构建的树就是这样的。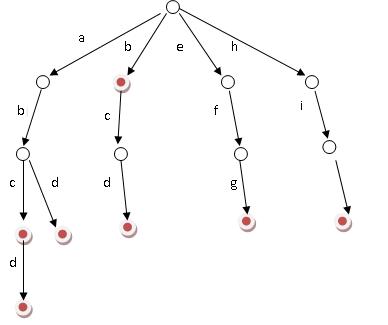

对于每一个节点，从根遍历到他的过程就是一个单词，如果这个节点被标记为红色，就表示这个单词存在，否则不存在。
那么，对于一个单词，我只要顺着他从跟走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。
这样一来我们询问和插入可以一起完成，所用时间仅仅为单词长度，在这一个样例，便是10。
我们可以看到，trie树每一层的节点数是26^i级别的。所以为了节省空间。我们用动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数×单词长度。

杭电AMC 1251 AC code

class node{
public:
    int count;
    node *son[26];//存放NODE的指针
    char core;
    node(char core){
        root=false;
        count=0;
        this->core=core;
        for(int i=0;i<26;++i) son[i]=NULL;
    }
    bool root;
    void add(string str,list<node> &trie);
    int getPreNum(string pre);
};

void node::add(string str, list<node> &trie){
    node *father=this;
    for(unsigned int i=0;i<str.size();++i){
        if(father->son[str[i]-'a']==NULL){
            node newson(str[i]);
            trie.push_back(newson);
            father->son[str[i]-'a']=&trie.back();
        }
        father->count++;
        father=father->son[str[i]-'a'];
    }
    father->count++;
}
int node::getPreNum(string pre){
    node *p=this;
    for(unsigned int i=0;i<pre.size();++i){
        if(p->son[pre[i]-'a']==NULL) return 0;
        p=p->son[pre[i]-'a'];
    }
    return p->count;
}