皮尔逊相关度评价
1、用在数据不是很规范的时候
2、最佳拟合线
3、夸大分值
4、皮尔逊积差系数
数学特征
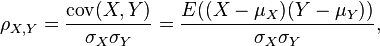
因为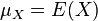 ,
,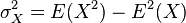 ,同样地,对于
,同样地,对于 ,可以写成
,可以写成

当两个变量的标准差都不为零,相关系数才有定义。从柯西-施瓦茨不等式可知,相关系数的绝对值不超过1。当两个变量的线性关系增强时,相关系数趋于1或-1。当一个变量增加而另一变量也增加时,相关系数大于0。当一个变量的增加而另一变量减少时,相关系数小于0。当两个变量独立时,相关系数为0.但反之并不成立。 这是因为相关系数仅仅反映了两个变量之间是否线性相关。比如说,X是区间[-1,1]上的一个均匀分布的随机变量。Y = X2. 那么Y是完全由X确定。因此Y 和X是不独立的。但是相关系数为0。或者说他们是不相关的。当Y 和X服从联合正态分布时,其相互独立和不相关是等价的。
当一个或两个变量带有测量误差时,他们的相关性就受到削弱,这时,“反衰减”性(disattenuation)是一个更准确的系数。
3:python的实现:

总结:
皮尔逊相关是对用户对相同的物品的喜欢程度,必需求出用户的共同物品,已经分别的和,按照公式就可以算出r


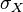 和
和  是
是
