42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

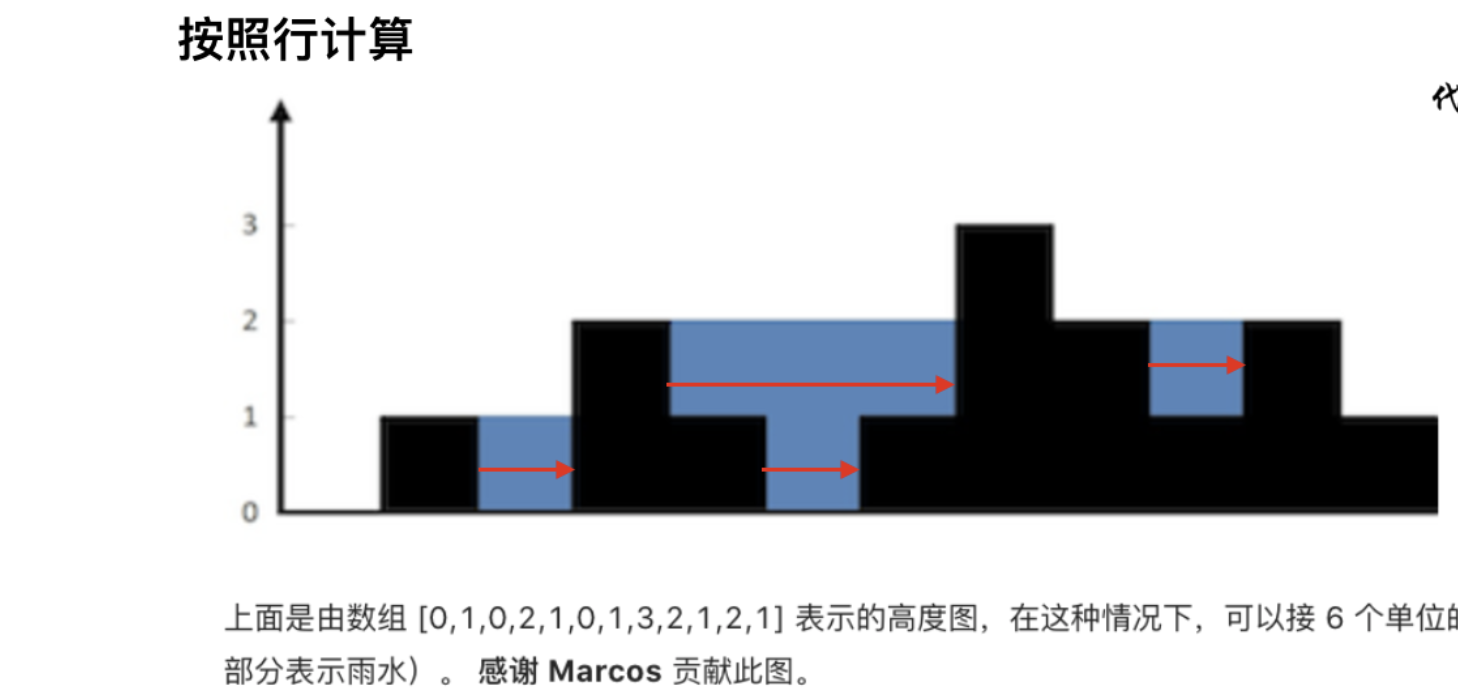
• 输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
• 输出：6
• 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）

 

双指针解法

按照列来计算的话，宽度一定是1了，我们再把每一列的雨水的高度求出来就可以了。

可以看出每一列雨水的高度，取决于，该列 左侧最高的柱子和右侧最高的柱子中最矮的那个柱子的高度

即： min(lHeight, rHeight) - height

class Solution {
    public int trap(int[] height) {
        return process(height);
    }

    private int process(int[] height){
        //按列计算
        //i:left Max. rightMax. h= min(leftMax,rightMax)-heigt[i]>0 sum+=h
        if(height.length<=2){
            return 0;
        }
        int sum=0;
        for(int i=1;i<height.length-1;i++){
            int leftMax=getRangeMax(height,0,i);
            int rightMax=getRangeMax(height,i,height.length-1);
            int h=Math.min(leftMax,rightMax)-height[i];
            if(h>0){
                sum+=h;
            }
            
        }
        return sum;
    }

    private int getRangeMax(int[] height,int L,int R){
        int max=0;
        for(int i=L;i<=R;i++){
            max=Math.max(max,height[i]);
        }
        return max;
    }
}

　　

动态规划解法

为了得到两边的最高高度，使用了双指针来遍历，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。

我们把每一个位置的左边最高高度记录在一个数组上（maxLeft），右边最高高度记录在一个数组上（maxRight）。这样就避免了重复计算，这就用到了动态规划。

当前位置，左边的最高高度是前一个位置的左边最高高度和本高度的最大值。

即从左向右遍历：maxLeft[i] = max(height[i], maxLeft[i - 1]);

从右向左遍历：maxRight[i] = max(height[i], maxRight[i + 1]);

这样就找到递推公式。

class Solution {
    public int trap(int[] height) {
        return process(height);
    }

    private int process(int[] height){
       //leftMax[i] 0....i 求得每个位置左边的最大值 leftMax[i]=Math.max(dp[i-1],height[i])
       //rightMax[i] i....R 求得每个位置右边的最大值 rightMax[i]=Maht.max(dp[i+1],heigth[i])
       //遍历1....i-1. Math.min(leftMax(i),rightMax(i))-heigt[i]
       //h >0 sum+=h
       int n=height.length;
       if(n<=2){
           return 0;
       }
       int[] leftMax=new int[n];
       leftMax[0]=height[0];
       for(int i=1;i<n;i++){
           leftMax[i]=Math.max(leftMax[i-1],height[i]);
       }

       int[] rightMax=new int[n];
       rightMax[n-1]=height[n-1];
       for(int i=n-2;i>=0;i--){
           rightMax[i]=Math.max(rightMax[i+1],height[i]);
       }

       int sum=0;
       for(int i=1;i<n-1;i++){
           int h=Math.min(leftMax[i],rightMax[i])-height[i];
           if(h>0) sum+=h;
       }

       return sum;
       
    }


}

　　

单调栈解法

单调栈是按照行方向来计算雨水

 

从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。

因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

遇到相同高度的柱子怎么办。

遇到相同的元素，更新栈内下标，就是将栈里元素（旧下标）弹出，将新元素（新下标）加入栈中。

例如 5 5 1 3 这种情况。如果添加第二个5的时候就应该将第一个5的下标弹出，把第二个5添加到栈中。

因为我们要求宽度的时候 如果遇到相同高度的柱子，需要使用最右边的柱子来计算宽度。

class Solution {
    public int trap(int[] height) {
        if(height.length<=2){
            return 0;
        }
        return process(height);
    }

    private int process(int[] height){
      //stack bigger.....smaller. when i the bigger then peek(),then pop,
      //i,popi,peeki, Math.min(height[i],hight[stack.peek()])-height[popi]-->h
      //w=i-peeki-1
      //h*w
      int sum=0;
      Stack<Integer> stack=new Stack<>();
      stack.push(0);
      for(int i=1;i<height.length;i++){
        
          if(height[i]<height[stack.peek()]){
              stack.push(i);
          }else if(height[i]==height[stack.peek()]){
              stack.pop();
              stack.push(i);
          }else{
              while(!stack.isEmpty() && height[i]>height[stack.peek()]){
                  int popi=stack.pop();
                  if(!stack.isEmpty()){
                      int h=Math.min(height[i],height[stack.peek()])-height[popi];
                      int w=i-stack.peek()-1;
                      int hold=h*w;
                      if(hold>0) sum+=hold;
                  }
               
              }
              stack.push(i);
          }
      }
      return sum;
    }


}