数据结构与算法(六)——图
数据结构与算法(六)——图
iwehdio的博客园:https://www.cnblogs.com/iwehdio/
Github:https://github.com/iwehdio/DSA_THU_DJH_asJava
1、图的基本术语
- 图 G = ( V ;E )。V 是顶点集,E 是连边集。用 n 来表示顶点的数量,用 e 来表示连边的数量。
- 在图中,两个顶点之间具有对应关系则称为邻接,用两个顶点间的连边表示。而两个顶点与这条连边具有的关系成为关联。
- 一般而言,不讨论自己与自己邻接的自环。
- 如果邻接顶点 u 和 v 的次序无所谓则( u,v )为无向边。
- 如果邻接顶点 u 和 v 的方向被规定了,则( u,v )为有向边。
- 所有边均无方向的图,称为无向图。所有边均有方向的图,称为有向图。有向边与无向边混合的成为混合图。有向图可以表示无向图和混合图。
- 路径是,一系列的顶点按照邻接关系构成的序列。如果一条路径中不含重复的节点,则称为简单路径。如果路径的起始节点都是一个节点,则称为环路。
- 如果一个有向图中不包含任何环路,则称为有向无环图。
- 欧拉环路:经过所有的有向边恰好一次的环路。哈密尔顿环路:经过所有的顶点恰好一次的环路。
2、图的实现
-
邻接矩阵:描述两个顶点之间的邻接关系。如果图中有 n 个顶点,对于有向图是 n 行 n 列的方阵,第 i 行第 j 列的元素,表征了第 i 个顶点与第 j 个顶点是否邻接。如果是带权图,只需将元素的值改为权值。
-
关联矩阵:描述顶点与边之间的关联关系。如果图中有 n 个顶点、e 条边,则为 n 行 e 列的矩阵,第 i 行第 j 列的元素,表征了第 i 个顶点是否与第 j 条边关联。每一列中只有两个元素不为0。
-
邻接表:描述每个顶点的邻接关系。如果图中有 n 个顶点,则为规模为 n 的向量。向量中的元素为列表,内容为该顶点所指向的邻接顶点。
-
顶点对象的实现:
typedef enum {UNDISCOVERED, DISCOVERED, VISITED} VStatus; //顶点三种状态的枚举 template <typename Tv> struct Vertex{ //顶点对象 Tv data; //数据 int inDegree, outDegree; //出入度(指出和指入的边数) VStatus status; //状态 int dTime, fTime; //时间标签(被发现和访问完毕的时刻) int parent; //父节点 int priority; //优先级 Vertex(Tv const &d): //构造新节点 data(d), inDegree(0), outDegree(0), status(UNDISCOVERED), dTime(-1), fTime(-1), parent(-1), priority(INT_MAX) {} } -
边对象的实现:
typedef enum {UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD} EStatus; template <typename Te> //边对象 struct Edge{ Te data; //数据 int weight; //权值 EStatus status; //类型 Edge(Te const &d, int w): //构造新边 data(d), weight(w), status(UNDETERMINED) {} } -
邻接矩阵的实现:
template <typename Tv, typename Te> class GraphMaxtrix : public Graph<Tv, Te>{ private: Vector< Vertex<Tv> > V; //顶点集 Vector< Vector< Edge<Te>* > > E; //边集,实际上就是邻接矩阵 public: /* 相关操作接口 */ GraphMaxtrix() { n = e = 0 ;} //构造 ~GraphMaxtrix(){ //析构 for(int j=0; j<n; j++) for(int k=0; k<n; k++) delete E[j][k]; //清除内存 } } -
顶点的静态操作:
//对于顶点的属性的查找,可以直接return其属性值 //枚举顶点的所有邻接顶点 int nextNbr(int i, int j){ //若已经枚举到邻居 j,则逆向查找下一个邻接 while((-1<j) && !exists(i, --j)); //逆向查找O(n) return j; } //使用邻接图可到O(1+outDegree(i)) int firstNbr(int i){ //查找第一个邻接 return nextNbr(i, n); } -
边的操作:
bool exists(int i, int j){ //判断边(i, j)是否存在 return (0<=i)&&(i<n)&&(0<=j)&&(j<n)&&E[i][j]!=null; } //如果边存在,则对于边的属性的查找,可以直接return其属性值 //插入边 void insert(Te const & edge, int w, int i, int j){ if(exists(i, j)) return; //判断是否以及存在 E[i][j] = new Edge<Te>(edge, w); //创建新边 e++; //更新边的数量 V[i].outDegree++; //分别更新边两个顶点的入度和出度 V[j].inDegree++; } //删除边,前提以及确认边存在 Te remove(int i, int j){ Te eBak = edge(i, j); //备份 delete E[i][j]; //删除边 E[i][j] = null; e--; V[i].outDegree--; //分别更新边两个顶点的入度和出度 V[j].inDegree--; return eBak; //返回被删除的边的信息 } -
顶点的动态操作:
//顶点的插入,邻接表的规模发生变化 int insert(Tv const & vertex){ for(int j=0; j<n; j++) E[j].insert(null); n++; //扩充邻接表中每个元素的规模 E.insert(Vector< Edge<Te>* >(n, n, null)); //扩充邻接表的规模 return V.insert(Vector<Tv>(vertex)); //扩充顶点列表的规模 } //顶点的删除 Tv remove(int i){ for(int j=0; j<n; j++){ if(exists(i, j)){ delete E[i][j]; V[j].inDegree--; //删除出边 } } E.remove(i); n--; //删除第 i 行 for(int j=0; j<n; j++){ if(exists(j, i)){ delete E[j].remove(i); //删除第 i 列 V[i].outDegree--; //删除所有入边 } } Tv vBak = vertex(i); V.remove(i); //删除顶点 return vBak; } //删除行和列的操作的区别? -
邻接矩阵表示法:
- 判断两点之间是否存在联边、获取顶点的出入度数、添加删除边后更新度数都是 O(1) 的时间复杂度。
- 空间复杂度总是 O(n^2) ,只与顶点数有关,与边数无关。对于平面图(不相邻的边不相交)的空间利用率很低。
3、广度和深度优先搜索
-
数据结构的简化分析:图 遍历 得到 树,树 遍历 得到 向量。
-
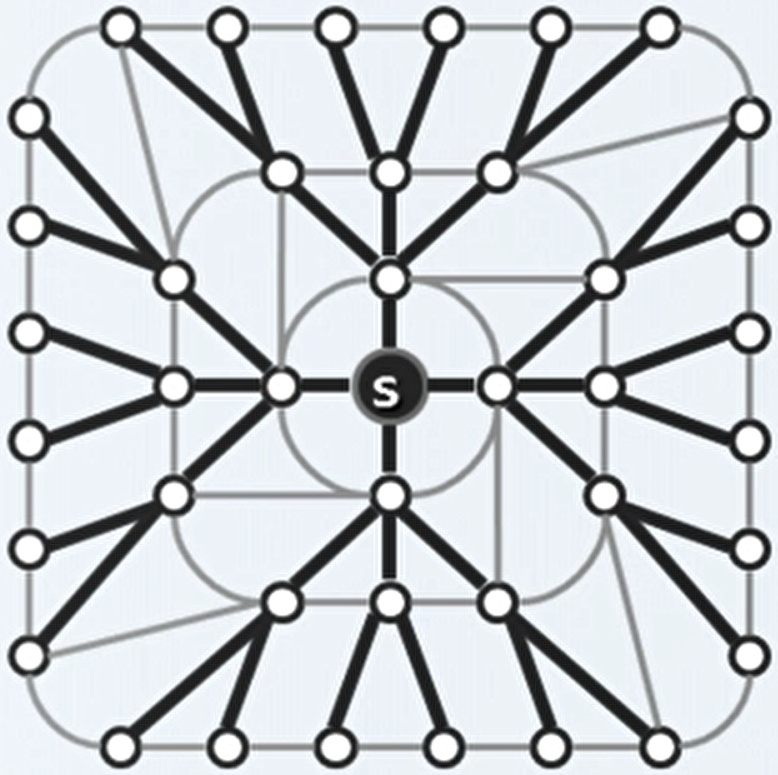
广度优先搜索:对于访问始自顶点为 s 的图。
-
访问顶点 s 。
-
依次访问 s 所有尚未访问的邻接顶点。
-
依次访问上述顶点尚未访问的邻接顶点。
-
如此反复直至没有尚未访问的邻接顶点。
-
-
广度优先搜索:得到了原图的一个极大无环图,即原图的支撑树(遍历了原图的所有顶点)。
-
树的层次遍历是广度优先搜索的特例。
-
实现:
template <typename Tv, typename Te> //顶点类型、边类型 void Graph<Tv, Te>::BFS(int v, int &clock){ //v是初始顶点 Queue<int> Q; //队列 status(v) = DISCOVERED; //顶点置为已发现并入队 Q.enqueue(v); while(!Q.empty()){ int v = Q.dequeue(); //取出队首顶点 dTime = ++clock; //打上时间标签 for(int u=fisrtNbr(v); -1<u; u=nextNbr(v, u)){ if(UNDISCOVERED == status(u)){ //如果u尚未被发现 status = DISCOVERED; //将u置为已发现并入队 Q.enqueue(u); status(v, u) = TREE; //将边(v,u)置为树边,即支撑树中的边 parent(u) = v; } else { status(v, u) = CROSS; //如果u已被发现或访问,则将边(v,u)置为跨边,不引入到支撑树中 } } status(v) = VISITED; //当前节点的邻接节点访问完毕 } } -
上述的广度优先算法,实际上是遍历了初始顶点所在的连通域,但一个图中可能有多个连通域。这时需要有多个初始顶点:
template <typename Tv, typename Te> void Graph<Tv, Te>::bfs(int s){ //s是初始顶点 reset(); //初始化 int clock = 0; int v = s; do{ //逐一检查所有顶点 if(UNDISCOVERED == status(v)){ //如果遇到尚未发现的顶点,则启动一次BFS BFS(v, clock); } } while(s!=(v=(++v%n))) //从s开始遍历所有顶点 } -
时间复杂度:理论上是 O(n^2) ,但是由于邻接矩阵中一个顶点的邻居在逻辑和物理上的连续性,实际效率可能达到 O( n+e ) 。如果使用邻接表可直接达到 O( n+e ) 。
-
最短路径:在图中,定义两个点之间的距离为其之间最短路径的距离。广度优先算法中,每个顶点到初始顶点的路径,都是其所有路径中到初始顶点的最短路径。
-
深度优先搜索:对于访问始自顶点为 s 的图。
- 访问顶点 s 。
- 若 s 有尚未被访问的邻接,则任选其一 u ,递归执行深度优先搜索。
- 否则,返回上一顶点。
-
实现:
template <typename Tv, typename Te> void Graph<Tv, Te>::DFS(int v, int &clock){ dTime(v) = ++clock; //打上发现时间标签 status(v) = DISCOVERED; //发现当前顶点v for(int u=firstNbr(v); -1<u; u=nextNbr(v, u)){ //枚举v的每一个邻居 switch(status(u)){ case UNDISCOVERED: //u未被发现 status(v, u) = TREE; //置为树边 parent(u) = v; DFS(u, clock); //递归 break; case DISCOVERED: //如果已被发现,在此处是后代指向祖先,标记为回边 status(v, u) = BACKWARD; break; default: //u已访问完毕(仅对于有向图有这种情况),视时间标签规定的承袭关系分为前向边或跨边 status(v, u) = dTime(v)<dTime(u) ? FOREARD : CROSS; break; } } status = VISITED; //v访问完毕 fTime(v) = ++clock; //打上完成时间标签 } -
可达域:对于有向图,可能由于指向的原因,在一个连通域内也无法从一个顶点遍历整个连通域,即具有多个可达域。这时可以借鉴BFS中遍历整个顶点向量的方式。
-
深度优先搜索的实例:无向图 视频的 P204,有向图 视频的P205。
-
嵌套引理:对于给定的有向图和其任一DFS森林。
-
定义顶点的活动期:
active[u]=(dTime[u], fTime[u])。 -
如果 u 是 v 的后代,当且仅当
acive[u] ⊆ acitve[v]。 -
如果 u 是 v 的祖先,当且仅当
acive[v] ⊆ acitve[u]。 -
如果 u 与 v 无关,当且仅当
active[u] ∩ acive[v] = Ø。
-
参考:数据结构与算法(清华大学C++描述):https://www.bilibili.com/video/av49361421
iwehdio的博客园:https://www.cnblogs.com/iwehdio/


