数据结构与算法（一）——绪论

数据结构与算法（一）——绪论
　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/
Github：https://github.com/iwehdio/DSA_THU_DJH_asJava

导图

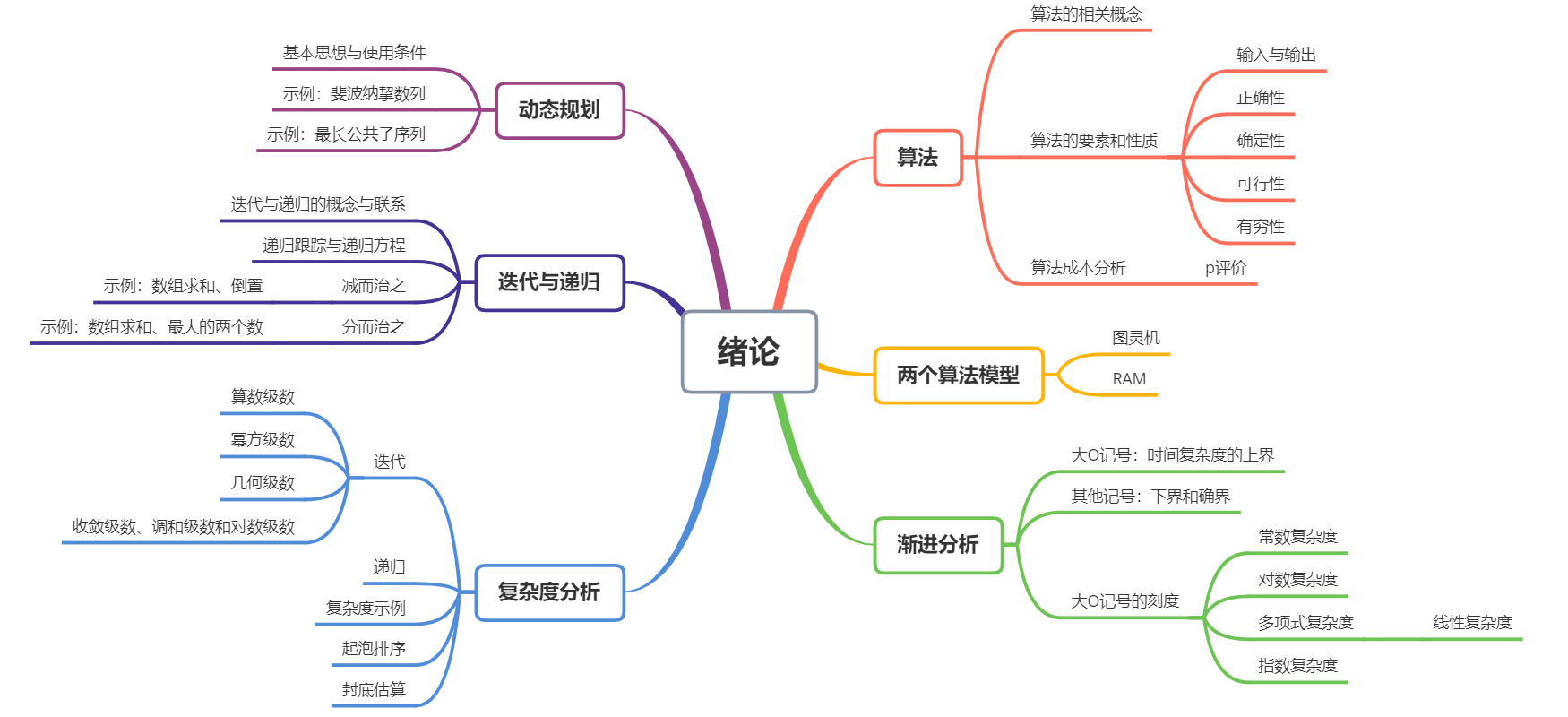
1、绪论

• 计算：借助某种工具，按照一定规则，以明确而机械的形式进行信息处理。

既是研究对象，也是研究目标。

研究计算规律和技巧，实现高效的计算，低资源消耗。

• 计算机：一种计算模型和信息处理工件。
• 算法：特定计算模型下，旨在解决特定问题的指令序列。
  • 输入，待处理的信息。
  • 输出：经处理的信息。
  • 正确性：可以解决的问题。
  • 确定性：任意算法都可以描述为一个由基本操作组成的序列。
  • 可行性：每一基本操作都可实现，并且可在常数时间内完成。
  • 有穷性：对任意输入，经过有穷步操作可以得到输出。
  • 程序未必是算法。
• 好的算法：效率，速度尽可能快，存储空间尽可能少。
• 计算模型的度量：算法分析
  • 正确性。
  • 性能（成本）：运行时间和所需存储空间。
  • 规模往往是决定计算成本的主要因素。
  • 空间复杂度一般指算法所需的额外的存储空间的大小。
• p评价算法的成本：
  • 令 T(P) = 用算法A求解问题P的实例所需的计算成本。
  • 则 T(n) 记为所有规模为n的实例P中，计算成本T(P)的最大值。
• 同一问题有多种算法：抽象出一个理想的平台或模型。

2、两个算法模型

• 图灵机：
  • 均匀划分单元格，每个单元格中一个字符，默认 ‘#’。
  • 字符的种类有限。
  • 读写头，总是对准某一个单元格，并可存储或改写。
  • 图灵机总是处于有限种状态的一种，每经过一个节拍，按照一定规则转向另一种状态。
  • 转换方式，根据输入转换状态的规则。
• RAM（Random Access Machine）：
  • 寄存器顺序编号，总数没有限制。
  • 每个基本操作仅需常数时间。

3、时间复杂度

• 以上两个模型是对一般计算工具的简化与重新。

• 算法的运行时间 转化为 算法需要执行的基本操作次数。

• 渐进分析：大 O 记号

  • 定义

    

  • 当问题规模足够大后，计算成本如何增长。

  • 常系数和低次项可忽略。

    

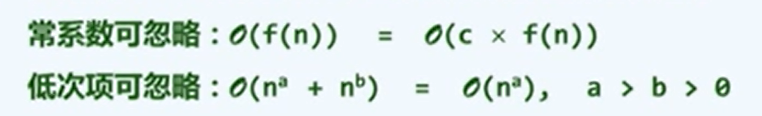
  • 可以认为是给出了时间复杂度的上界。

    

• 渐进分析的其他记号：

  • Ω 时间复杂度的的下界。
  • Θ 时间复杂度的确界。

• 大 O 记号的刻度：

  • 常数复杂度：O(1)；这类算法的效率最高。
    • 一般是顺序执行。
    • 循环、分支转向和递归有时也可几乎达到常数复杂度。
  • 对数复杂度：O(log n)；也很高效，复杂度无限接近常数，比所有多项式复杂度都低。
    • 常底数无所谓。
    • 常数次幂无所谓。
    • 对数多项式可进行简化。
  • 多项式复杂度：O(n^c)；
    • 线性复杂度O(n)；
  • 指数复杂度：O(2^n)；计算成本一般认为不可忍受，比所有多项式复杂度都高。
    • 许多问题的O(2^n)算法一般是显而易见的，但O(n^c)的算法较难找到。

4、算法分析

• 两个任务 = 正确性（不变性 × 单调性）+ 复杂度。

• 复杂度分析：

  • 迭代：级数求和。
  • 递归：递归跟踪 + 递归方程。

• 级数：

  • 算术级数（等差数列的前 n 项和）：与末项平方同阶。

  • 幂方级数（从1到n的 k 次方的前 n项和）：比幂次高出一阶。

  • 几何级数（等比数列的前 n 项和）：与末项同阶。

  • 收敛级数（存在极限）：常数复杂度。分数操作次数表征概率。

  • 未必收敛当时长度有限，具体分析。

    

• 以下程序的复杂度都是O(n^2)：

  //No.1
  for(int i=0;i<=n;i++)
  for(int j=1;j<=n;j++)     
  //No.2
  for(int i=0;i<=n;i++)
  for(int j=1;j<i;j++) 
  //No.3
  for(int i=0;i<=n;i++)
  for(int j=1;j<i;j+=200) 
  

• 以下程序的复杂度是O(n)：

  for(int i=0;i<=n;i<<=1)
  for(int j=1;j<i;j++)
  

  图解：

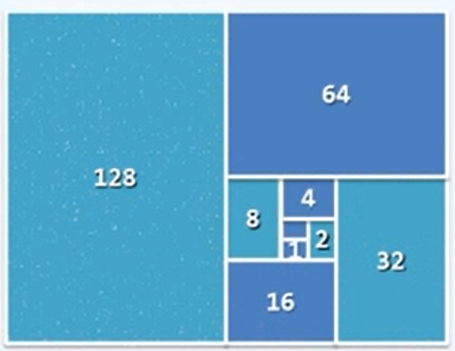
• 以下程序的复杂度是O(log n * 2^log n)：

  for(int i=0;i<=n;i++)
  for(int j=1;j<i;j+=j)
  

  • 可以看出，i 取3_4、58、9~16 时，第二层循环中的操作数是相同的。
  • 先确定每次操作数为 k 的通项公式：k * 2^(k-1)。
  • 操作数是几何级数，和与其末项 log2 n 同阶。
  • 代入 k 可得O(log n * 2^log n)。

• 起泡排序：

  • 问题：给定n个整数，将它们按（非降）序排列。
  • 观察：有序 / 无序序列中，任意 / 总有一对相邻元素顺序/逆序。
  • 扫描交换：依次比较每一对相邻元素，如有必要，交换之若整趟扫描都没有进行交换，则排序完成；否则，再做一趟扫描交换。
  • 不变性：经k轮扫描交换后，最大的k个元素必然就位。例如，经过第一轮扫描，最大的元素必然在序列的最后；经过第二轮扫描，第二大的元素必然在序列的倒数第二个。
  • 单调性：经k轮扫描交换后，问题规模缩减至n-k。同不变形，因为最大的元素已经在正确的位置。
  • 正确性：经至多n趟扫描后，算法必然终止，且能给出正确解答。
  • 复杂度是 O(n^2)。
  • 示意图：
  

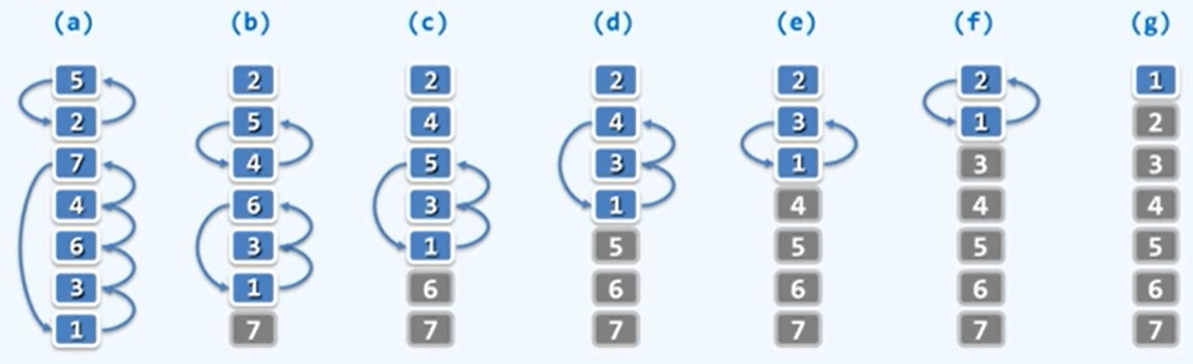
• 封底估算：

  • 建立封底估算时间概念：一天 ~ 10^5 s , 一世纪 ~ 10^9 s 。

5、迭代与递归

• 递归：重复调用函数自身实现循环。不断深层调用函数，直到函数有返回时逐层返回。可以认为是树状结构。

• 迭代：利用变量的原值推出新值，函数内某段代码实现循环。可以认为是环状结构。

• 所有的迭代可以转换为递归，但递归不一定可以转换为迭代。

• 减而治之的思想：划分为两个子问题，其中一个是平凡问题（复杂度小于原问题），另一个是原问题规模缩减的问题。

• 递归跟踪：
  

• 递归方程：T(n)=T(n-1)+T(0)，为了求解规模为n的问题，分为求规模为n-1的问题，再加上平凡问题所需的时间T(0)。平凡问题也可成为递归基，复杂度为T(0)。

• 例1：数组求和：线性递归(复杂度与直接求和相同，还是O(n))

  int sum(int A[], int n){
      return (n < 1) ? 0 : sum(A, n-1)+A[n-1];
  }
  

• 例2：数组倒置

  void reverse(int* A, int lo, int hi){
      if(lo < hi){
          swap(A[lo], A[hi]);
          reverse(A, lo+1, hi-1);
      }
  }
  

• 分而治之的思想：划分为多个（一般是两个）规模相当的问题。

• 例1：数组求和：二分递归(复杂度与直接求和相同，还是O(n))

  int sum(int A[], int lo, int hi){
      if(lo == hi){
          return A[lo];
      }
      int mi = (lo + hi) >> 1;
      return sum(A, lo, mi) + sum(A, mi+1, hi);
  }
  

• 例2：Max2：从数组区间中找出最大的两个整数。

  void max2(int A[], int lo, int hi, int &x1, int &x2){
      if(A[x1 = lo] < A[x2 = lo + 1]) swap(x1, x2);
      for(int i = lo + 2; i < hi; i++)
          if(A[x2] < A[i])
              if(A[x1] < A[x2 = i])
                  swap(x1, x2);
  }
  

6、动态规划

• 基本思想：问题的最优解如果可以由子问题的最优解推导得到，则可以先求解子问题的最优解，在构造原问题的最优解；若子问题有较多的重复出现，则可以自底向上从最终子问题向原问题逐步求解。

• 使用条件：可分为多个相关子问题，子问题的解被重复使用。

• 斐波那契数列的计算：(复杂度为O(2^n))

  int fib(int n){
      return (2 > n) ? n : fib(n-1) + fib(n-2);
  }
  

• 改进1：制表备查.。

• 改进2：颠倒计算方向：自顶而下递归，为自底而上迭代。(复杂度O(n))

  f = 1; g = 0;		//fib(0), fib(-1)
  int fib(int n){
      while(0 < n--){
          g = g + f;
          f = g - f;
      }
      return g;
  }
  

• LCS，最长公共子序列。

• 子序列：由序列中若干字符，按相对次序构成。

• 最长公共子序列：两个序列公共子序列中的最长值（可能有多个，可能有歧义）。

  • 记为对序列A[0,n]和B[0,m]，最长公共子序列为LCS(A,B)。

  • 递归基：若 n=-1或m=-1，则取空序列("")。

  • 减而治之：如果A[n]='X'=B[m]，即两个输入序列的最后一位相同，则取做LCS(A[0,n),B[0,m))+'X'。也就是说去掉相同的最后一位，同时向前递归。

    

  • 分而治之：如果A[n]≠B[m]，则在LCS(A[0,n],B[0,m)与LCS(A[0,n),B[0,m])中取更长者。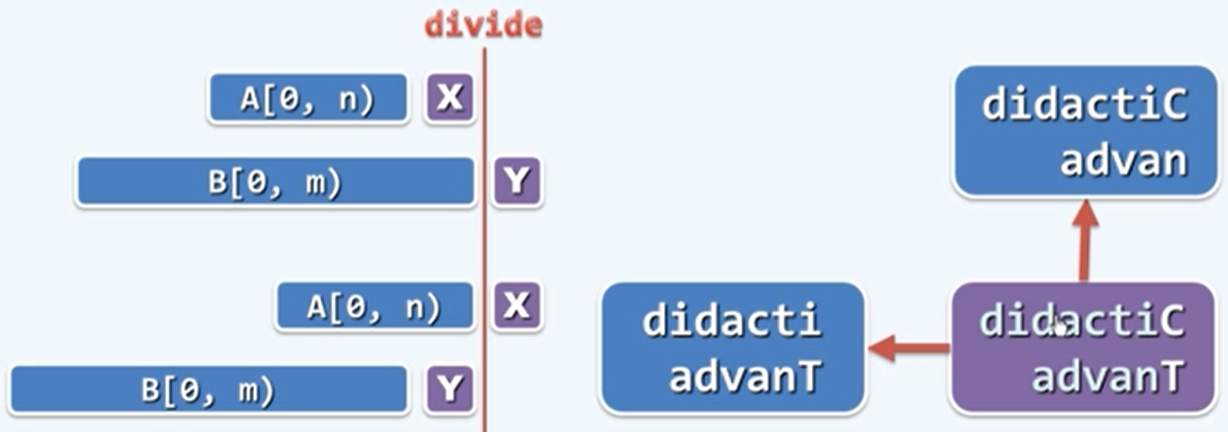

    

  • 实际上，这样的递归算法的复杂度为O(2^n)，需要用动态规划。

    1. 将所有的子问题列成一张表。
    2. 颠倒计算方向，从LCS(A[0],B[0])出发，依此计算所有项。
  

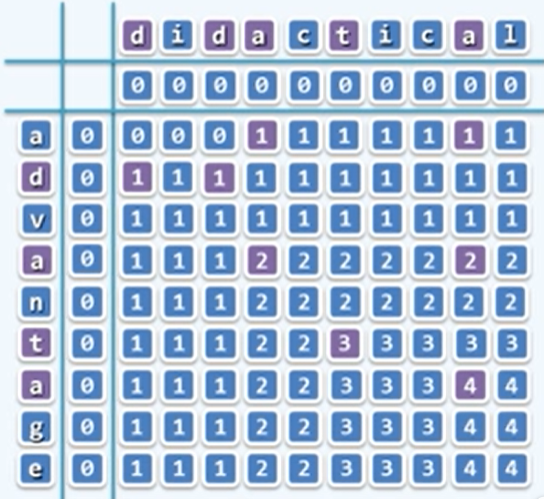
参考：数据结构与算法（清华大学C++描述）：https://www.bilibili.com/video/av49361421


iwehdio的博客园：https://www.cnblogs.com/iwehdio/