Python中的概率分布API

数理统计（二）——Python中的概率分布API

　　iwehdio的博客园：https://www.cnblogs.com/iwehdio/

 

　　数理统计中进行假设检验需要查一些分布的上分位数表。在scipy的stats统计模块中，有关于数理统计中一些概率分布的API，可求得分布的概率分布函数、概率密度函数和上分位数等。选常用的正态分布、t分布、F分布、卡方分布和伽马分布做使用介绍。

 

　　导入模块，并说明各个模块对应的分布：

from scipy import stats

# 正态分布
stats.norm

# t分布
stats.t

# F分布
stats.f

# 卡方分布
stats.chi2

# 伽马分布
stats.gamma

 

　　

1、正态分布

　　正态分布的模块名为stats.norm。在stats模块中，都是对对应分布的模块取方法来实现的，常用的三个方法如下：

功能	方法	表达式
求概率分布函数 F(x)	.cdf(x;L,S)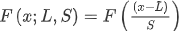
求概率密度函数 f(x)	.pdf(x;L,S)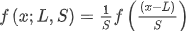
求置信度为α的上分位数 Z(α)	.isf(α；L,S)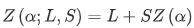

　　其中x为自变量的值，α为置信度，L和S为分布参数，默认L=0，S=1。

 

　　对于正态分布，可以求出其在x=0.5，α=0.05，均值为2，方差为3下的概率分布、概率密度和上分位数。

# 概率分布函数
>>> stats.norm.cdf(0.5,2,3)
0.3085375387259869

# 概率密度函数
>>> stats.norm.pdf(0.5,2,3)
0.11735510892143318

# 上分位数
>>> stats.norm.isf(0.05,2,3)
6.934560880854418

 

　　画概率分布曲线、概率密度曲线：

# 概率分布曲线
x=np.linspace(0,8,2000)
y=stats.norm.cdf(x,2,3)
plt.plot(x,y)
plt.title('Norm_F')

# 概率密度曲线
x=np.linspace(-6,10,2000)
y=stats.norm.pdf(x,2,3)
plt.plot(x,y)
plt.title('Norm_f')

 

　　正态分布的概率分布曲线：

 

　　正态分布的概率密度曲线：

　　

 

 2、其他分布

　　其他分布的操作与正态分布类似。

　　

　　①、t分布

 

# 概率分布函数
x=np.linspace(-5,5,2000)
y=stats.t.cdf(x,5)
plt.plot(x,y)
plt.title('t_F')

# 概率密度函数
x=np.linspace(-5,5,2000)
y=stats.t.pdf(x,5)
plt.plot(x,y)
plt.title('t_f')

 

 

　　②、F分布

# 概率分布函数
x=np.linspace(-1,8,2000)
y=stats.f.cdf(x,5,8)
plt.plot(x,y)
plt.title('f_F')

# 概率密度函数
x=np.linspace(-1,8,2000)
y=stats.f.pdf(x,5,8)
plt.plot(x,y)
plt.title('f_f')

　　

 

 　　③、卡方分布

　　

 

　　④、伽马分布

　　

 

　　⑤、更多概率分布见：

　　scipy官方文档：连续统计分布 https://docs.scipy.org/doc/scipy-1.4.0/reference/tutorial/stats/continuous.html

 

 参考：scipy官方文档：连续统计分布 https://docs.scipy.org/doc/scipy-1.4.0/reference/tutorial/stats/continuous.html

 

 iwehdio的博客园：https://www.cnblogs.com/iwehdio/