用Python做方差分析
iwehdio的博客园:https://www.cnblogs.com/iwehdio/
方差分析可以用来推断一个或多个因素在其状态变化时,其因素水平或交互作用是否会对实验指标产生显著影响。主要分为单因素方差分析、多因素无重复方差分析和多因素重复方差分析。
做数理统计课后题,发现方差分析计算比较麻烦,想用Python调包实现。但是发现大多教程对参数的讲解不是很清楚,在此做记录。
主要用到的库是pandas和statsmodels。简要流程是,先用pandas库的DataFrame数据结构来构造输入数据格式。然后用statsmodels库中的ols函数得到最小二乘线性回归模型。最后用statsmodels库中的anova_lm函数进行方差分析。
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
首先,是输入的数据格式。使用pandas的DataFrame,每一行为一次试验的因素水平和试验结果。以下图中的题目为例。
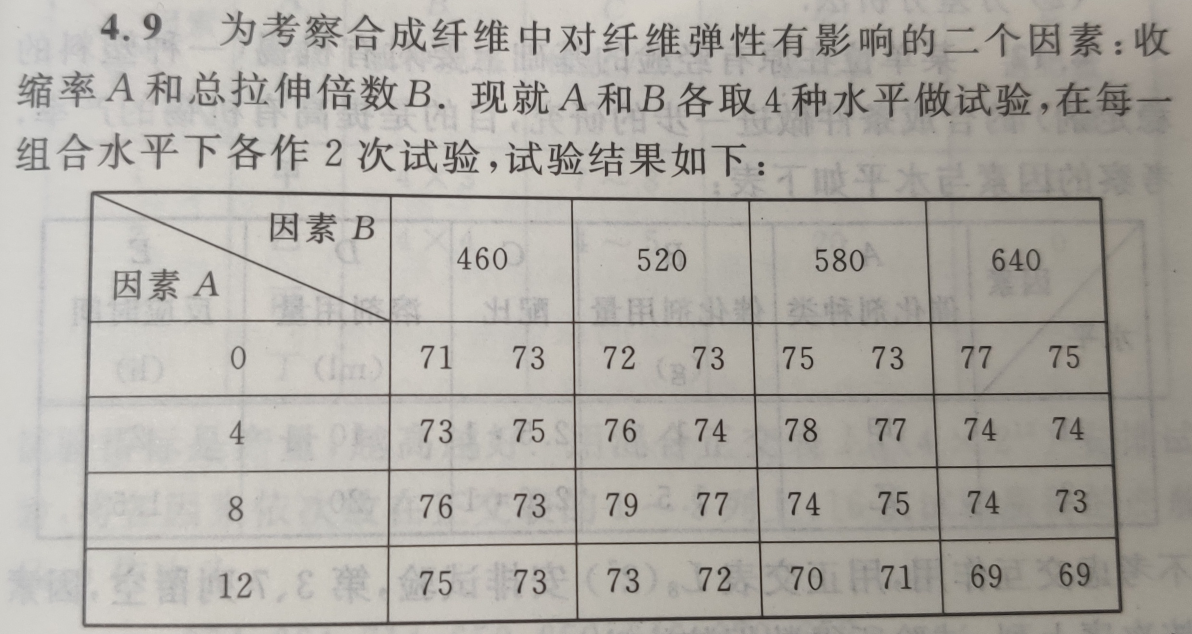
则对于因素A和因素B即结果R可表示为如下的DataFrame:
data = pd.DataFrame([[1, 1, 32],
[1, 2, 35],
[1, 3, 35.5],
[1, 4, 38.5],
[2, 1, 33.5],
[2, 2, 36.5],
[2, 3, 38],
[2, 4, 39.5],
[3, 1, 36],
[3, 2, 37.5],
[3, 3, 39.5],
[3, 4, 43]],
columns=['A', 'B', 'value'])
第一列为因素A的水平,第二列为因素B的水平,第三列为试验结果。在方差分析中,只关心每次试验中因素水平是否相同,所以我们可以把较为复杂的因素水平抽象为标签值 1,2,3。
然后,输入ols函数。主要用到该函数的两个参数,formula和data。
formula指定了:
①试验结果是哪一列。
②需要计算的是哪几个因素水平对结果的影响。
③是否计算交互作用。
formula的类型为字符串,输入格式为如果试验结果的列名为‘value’,需要计算的因素的列名为‘A’和‘B’,则示例如下。
# 因素A的水平对结果的影响
'value ~ C(A)'
# 因素A和因素B的水平对结果的影响
'value ~ C(A) + C(B)'
# 因素A和因素B以及A和B的交互作用的水平对结果的影响
'value ~ C(A) + C(B) + C(A)*C(B)'
# 多因素无重复试验,不计算交互作用的影响
model = ols('value~C(A) + C(B)', data=data[['A', 'B', 'value']]).fit()
anovat = anova_lm(model)
print(anovat)
data为之前生成的DataFrame中选出的进行分析所需要的列,实际上ols是通过DataFrame的列名来获得试验结果和因素水平的数据的。
最后用ols函数进行最小二乘线性拟合,用anova_lm函数进行方差分析并输出结果。之前题目输出的结果为:

Residual表示误差,df表示自由度,sum_sq表示离差平方和,mean_sq表示均方离差,F表示F值,PR(>F)表示F值所对应的显著水平α。
进行单因素多方差分析,将formula中的C(B)去掉即可。如果是对于有重复的多因素方差分析,示例如下:

结果为:
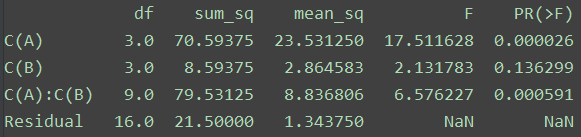
参考:施雨 《应用数理统计(西安交通大学)》 课后习题 4.1,4.3,4.5,4.6,4.9
python做单因素方差分析:https://www.cnblogs.com/jin-liang/p/9852321.html
Python数据科学:方差分析:https://blog.csdn.net/Kaitiren/article/details/85066793
iwehdio的博客园:https://www.cnblogs.com/iwehdio/


