java排序算法总结

总结排序算法前，先对排序算法中出现的术语进行说明。

1.术语说明

• 稳定与不稳定：a在b前，若a=b，排序后a一定还在b前，这就说明稳定
• 内外排序：基于内存排序，就是内排序
• 时间复杂度：算法耗费的时间
• 空间复杂度：耗费内存的大小

2.算法分类

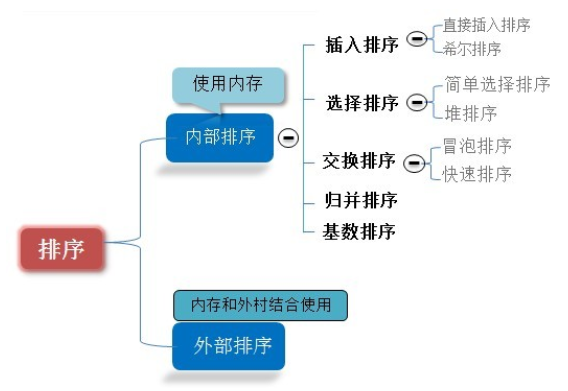
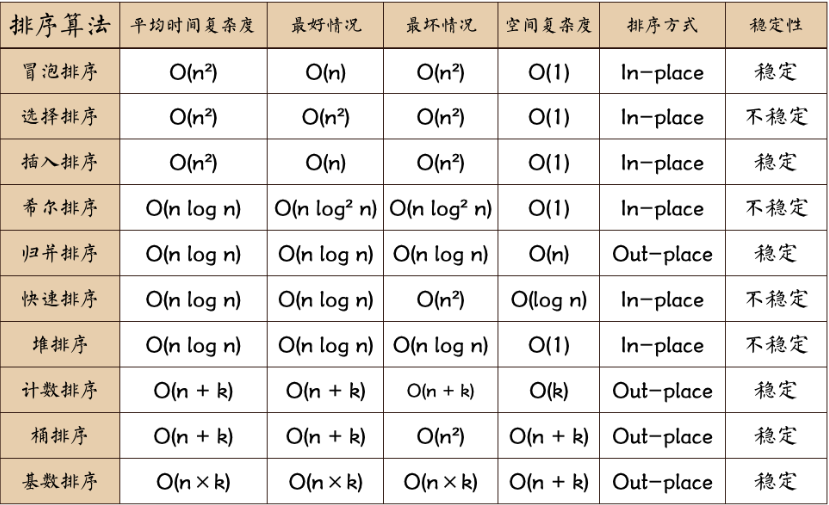
下面详细介绍算法。

1.冒泡排序

这是最常见的排序。从第一个到最后一个元素，相邻元素比大小，互换位置。

举例说明：

    public static int[] bubble(int[] arr){
        if (arr.length == 0) {
            return arr;
        }
        for (int i = 0; i < arr.length; i++) {
            for (int j = i; j < arr.length; j++) {
                if (arr[j] < arr[i]) {
                    int temp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = temp;
                }
            }
        }
        return arr;
    

2.快速排序

它是冒泡排序的升级版。原理，随机找出一个元素，把数列分成两部分，使一部分比另一部分元素小，按照同样的方法，把子数列再分成更小的子数列，直到不能分为止。

举例说明：

    public static int[] quick(int[] arr, int start, int end) {
        if (arr.length < 1 || start < 0 || end > arr.length || start > end) {
            return null;
        }
        int point = partition(arr, start, end);
        //左子序排序
        if (point > start) {
            quick(arr, start, point - 1);
        }
        //右子序排序
        if (point < end) {
            quick(arr, point + 1, end);
        }
        return arr;
    }

    private static int partition(int[] arr, int start, int end) {
        int temp = (int) (start + Math.random() * (end - start + 1));
        int index = start - 1;
        swap(arr,temp,end);
        for (int i = start; i <= end; i++) {
            if (arr[i] <= arr[end]) {
                index++;
                if (i > index) {
                    swap(arr,i,index);
                }
            }
        }
        return index;

    }

    private static void swap(int[] arr, int i, int j) {
        if (arr != null && arr.length > 0) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

3.堆排序

堆物理上是完全二叉树。数列构成大顶堆。将堆顶与末尾元素交换，将剩余元素重新构成大顶堆。将堆顶与末尾元素交换，以此类推。

举例说明：

    private static void swap(int[] arr, int i, int j) {
        if (arr != null && arr.length > 0) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }

    public static int[] heap(int[] arr) {
        len = arr.length;
        if (len < 1) {
            return arr;
        }
        buildMaxHeap(arr);
        while (len > 0) {
            //堆顶与末尾元素交换
            swap(arr,0,len - 1);
            len--;
            adjustHeap(arr, 0);
        }
        return arr;
    }

    private static void adjustHeap(int[] arr, int i) {
        int maxIndex = i;
        //右节点
        if (i * 2 + 2 < len && arr[i * 2 + 2] > arr[maxIndex]) {
            maxIndex = i * 2 + 2;
        }
        //左节点
        if (i * 2 + 1 < len && arr[i * 2 + 1] > arr[maxIndex]) {
            maxIndex = i * 2 + 1;
        }
        if (maxIndex != i) {
            swap(arr,maxIndex,i);
            adjustHeap(arr,maxIndex);
        }
    }

    private static void buildMaxHeap(int[] arr) {
        for (int i = (len/2 - 1); i >= 0; i--) {
            adjustHeap(arr,i);
        }
    }

这里有一个问题，表示右节点2*i+2，为什么不能是2*1？

4.选择排序

找到最值放到起始位置，再次剩余元素中找最值放在已排序序列末尾。以此类推。

举例说明：

    public static int[] select(int[] arr) {
        if (arr.length == 0) {
            return arr;
        }
        for (int i = 0; i < arr.length; i++) {
            int mixIndex = i;
            for (int j = i; j < arr.length; j++) {
                if (arr[j] < arr[mixIndex]) {
                    mixIndex = j;
                }
            }
            swap(arr,mixIndex,i);
        }
        return arr;
    }

5.插入排序

将数列第一个元素认为有序，在已排序列中从后向前(从前往后)寻找插入位置插入数据。

举例说明：

    public static int[] insert(int[] arr) {
        if (arr.length == 0) {
            return arr;
        }
        int curr;
        for (int i = 0; i < arr.length - 1; i++) {
            curr = arr[i + 1];
            int preIndex = i;
            while (preIndex >= 0 && curr < arr[preIndex]) {
                arr[preIndex + 1] = arr[preIndex];
                preIndex--;
            }
            arr[preIndex + 1] = curr;
        }
        return arr;
    }

 

6.希尔排序

按下标的一定增量分组，对每组使用插入排序排序。增量减少，每组包含元素增多，对每组使用插入排序排序。以此类推，直到增量为1。

举例说明：

    public static int[] shell(int[] arr) {
        int len = arr.length;
        int temp,gap = len / 2;
        while (gap > 0) {
            for (int i = gap; i < len; i++) {
                temp = arr[i];
                int preIndex = i - gap;
                while (preIndex >= 0 && arr[preIndex] > temp) {
                    arr[preIndex + gap] = arr[preIndex];
                    preIndex -= gap;
                }
                arr[preIndex + gap] = temp;
            }
            gap /= 2;
        }
        return arr;
    }

 

7.归并排序

先使每个子数列有序，再使子序列间有序，最后合并。

举例说明：

 

/**
     * 归并排序
     *
     * @param array
     * @return
     */
    public static int[] MergeSort(int[] array) {
        if (array.length < 2) return array;
        int mid = array.length / 2;
        int[] left = Arrays.copyOfRange(array, 0, mid);
        int[] right = Arrays.copyOfRange(array, mid, array.length);
        return merge(MergeSort(left), MergeSort(right));
    }
    /**
     * 归并排序——将两段排序好的数组结合成一个排序数组
     *
     * @param left
     * @param right
     * @return
     */
    public static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        for (int index = 0, i = 0, j = 0; index < result.length; index++) {
            if (i >= left.length)
                result[index] = right[j++];
            else if (j >= right.length)
                result[index] = left[i++];
            else if (left[i] > right[j])
                result[index] = right[j++];
            else
                result[index] = left[i++];
        }
        return result;
    }

/**
     * 归并排序
     *
     * @param array
     * @return
     */
    public static int[] MergeSort(int[] array) {
        if (array.length < 2) return array;
        int mid = array.length / 2;
        int[] left = Arrays.copyOfRange(array, 0, mid);
        int[] right = Arrays.copyOfRange(array, mid, array.length);
        return merge(MergeSort(left), MergeSort(right));
    }
    /**
     * 归并排序——将两段排序好的数组结合成一个排序数组
     *
     * @param left
     * @param right
     * @return
     */
    public static int[] merge(int[] left, int[] right) {
        int[] result = new int[left.length + right.length];
        for (int index = 0, i = 0, j = 0; index < result.length; index++) {
            if (i >= left.length)
                result[index] = right[j++];
            else if (j >= right.length)
                result[index] = left[i++];
            else if (left[i] > right[j])
                result[index] = right[j++];
            else
                result[index] = left[i++];
        }
        return result;
    }

 

8.计数排序

数列最值差值范围申请额外空间，将元素出现的次数记录元素值对应的额外空间，计算元素位置，将元素移到计算出的位置上。

举例说明：

{
        if (arr.length == 0) {
            return arr;
        }
        int bias, min = arr[0], max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
            if (arr[i] < min) {
                min = arr[i];
            }
        }
        bias = 0 - min;
        //确定统计数组的长度
        int[] bucket = new int[max - min + 1];
        Arrays.fill(bucket,0);
        //填充统计数据
        for (int i = 0; i < arr.length; i++) {
            bucket[arr[i] + bias]++;
        }
        int index = 0,i = 0;
        while (index < arr.length) {
            if (bucket[i] != 0) {
                arr[index] = i - bias;
                bucket[i]--;
                index++;
            } else {
                i++;
            }
        }
        return arr;
    }

9.桶排序

设置bucketsize（每个桶能放多少不同数值），把数据依次放入对应的桶中。对每个桶排序，最后拼接数据。

举例说明：

{
        if (arr == null || arr.size() < 2) {
            return arr;
        }
        int max = arr.get(0), min = arr.get(0);
        for (int i = 0; i < arr.size(); i++) {
            if (arr.get(i) >max) {
                max = arr.get(i);
            }
            if (arr.get(i) < min) {
                min = arr.get(i);
            }
        }
        int bucketCount = (max - min) / bucketsize + 1;
        List<List<Integer>> bucketArr = new ArrayList<>(bucketCount);
        List<Integer> result = new ArrayList<>();
        for (int i = 0; i < bucketCount; i++) {
            bucketArr.add(new ArrayList<Integer>());
        }
        for (int i = 0; i < arr.size(); i++) {
            bucketArr.get((arr.get(i) - min) / bucketsize).add(arr.get(i));
        }
        for (int i = 0; i < bucketCount; i++) {
            if (bucketsize == 1) {
                for (int j = 0; j < bucketArr.get(i).size(); j++) {
                    result.add(bucketArr.get(i).get(j));
                }
            } else {
                if (bucketCount == 1) {
                    bucketsize--;
                }
                List<Integer> temp = bucket(bucketArr.get(i), bucketsize);
                for (int j = 0; j < temp.size(); j++) {
                    result.add(temp.get(j));
                }
            }
        }
        return result;
    }

10.基数排序

 按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

/**
     * 基数排序
     * @param array
     * @return
     */
    public static int[] RadixSort(int[] array) {
        if (array == null || array.length < 2)
            return array;
        // 1.先算出最大数的位数；
        int max = array[0];
        for (int i = 1; i < array.length; i++) {
            max = Math.max(max, array[i]);
        }
        int maxDigit = 0;
        while (max != 0) {
            max /= 10;
            maxDigit++;
        }
        int mod = 10, div = 1;
        ArrayList<ArrayList<Integer>> bucketList = new ArrayList<ArrayList<Integer>>();
        for (int i = 0; i < 10; i++)
            bucketList.add(new ArrayList<Integer>());
        for (int i = 0; i < maxDigit; i++, mod *= 10, div *= 10) {
            for (int j = 0; j < array.length; j++) {
                int num = (array[j] % mod) / div;
                bucketList.get(num).add(array[j]);
            }
            int index = 0;
            for (int j = 0; j < bucketList.size(); j++) {
                for (int k = 0; k < bucketList.get(j).size(); k++)
                    array[index++] = bucketList.get(j).get(k);
                bucketList.get(j).clear();
            }
        }
        return array;
    }