RNN神经网络-简单的序列预测问题
RNN神经网络-简单的序列预测问题
RNN神经网络能够实现记忆功能,被广泛地应用在时间序列分析上,在NLP、语音识别等方向有许多的应用。
原理:
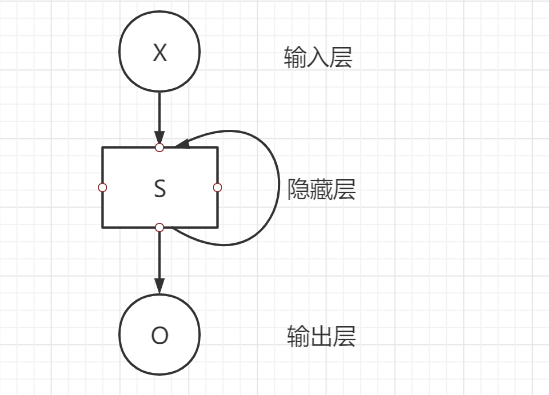
RNN神经网络是一个序列结构,在处理数据时,\(S_t\)的值不仅取决于当前的输入,还取决于上一层的输出,因此其在处理序列数据具有很明显的优势。
计算公式:
\(h_t=tanh(w_{ih} x_t+b_{ih}+w_{hh} h_{t-1}+b_{hh})\)
\(x_t\)是上一层时刻\(t\)的隐状态,或者是第一层在时刻\(t\)的输入。
使用Pytorch中RNN神经网络实现一个简单的序列预测问题
1. 构造初始数据
#训练数据横轴上的取值
x_num=50
#隐藏层特征数量
hidden_size=16
#输入x的特征数量。
input_size=1
output_size=1
#随机生成正弦函数左边界
start = np.random.randint(5) # random in [0,3]
#将序列划分为等间距的区间
x_value = np.linspace(start,start+10,x_num)
#生成训练数据
data = np.sin(x_value)
#embedding,将数据转换为100*1的矩阵
data = data.reshape(x_num,1)
#输入是0-70的数据值
x = torch.tensor(data[:49]).float().view(1,x_num-1,1)
#预测30-100的数据值
y = torch.tensor(data[1:]).float().view(1,x_num-30,1)
note:
-
由于网络需要训练很多次来降低误差,在训练时,需要让此左边界值是个随机值,否则每次的训练数据一致,导致模型过拟合。
-
view(**args*) → Tensor
返回一个有相同数据但大小不同的tensor。 返回的tensor必须有与原tensor相同的数据和相同数目的元素,但可以有不同的大小。
2. 构建网络
#定义网络
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
self.rnn = nn.RNN(
input_size = input_size,#输入x的特征数量
hidden_size = hidden_size,#隐藏层的特征数量
num_layers=1,#RNN层数
batch_first=True,#[batch_size, time_step, feature]
)
self.linear = nn.Linear(hidden_size,output_size)
#定义了每次执行的 计算步骤
def forward(self,x,hidden_prev):
out, hidden_prev = self.rnn(x,hidden_prev)
out = out.view(-1,hidden_size)
out = self.linear(out)
#在指定维度前插入维度1
out = out.unsqueeze(dim=0) # [1,seq,1]
return out,hidden_prev
note:
-
class torch.nn.RNN( args, * kwargs)[source]
将一个多层的 RNN,激活函数为tanh或者ReLU,用于输入序列。
对输入序列中每个元素,RNN每层的计算公式为 $ h_t=tanh(w_{ih} x_t+b_{ih}+w_{hh} h_{t-1}+b_{hh}) $ \(h_t\)是时刻\(t\)的隐状态。 \(x_t\)是上一层时刻\(t\)的隐状态,或者是第一层在时刻\(t\)的输入。如果nonlinearity=relu,那么将使用relu代替tanh作为激活函数。
参数:
-
input_size – 输入x的特征数量。
-
hidden_size – 隐层的特征数量。
-
num_layers – RNN的层数。
-
nonlinearity – 指定非线性函数使用tanh还是relu。默认是tanh。
-
bias – 如果是False,那么RNN层就不会使用偏置权重 \(b_ih\)和\(b_hh\),默认是True
-
batch_first – 如果True的话,那么输入Tensor的shape应该是[batch_size, time_step, feature],输出也是这样。
-
dropout – 如果值非零,那么除了最后一层外,其它层的输出都会套上一个dropout层。
-
bidirectional – 如果True,将会变成一个双向RNN,默认为False。
-
h_0 (num_layers * num_directions, batch, hidden_size): 保存着初始隐状态的tensor
-
output (seq_len, batch, hidden_size * num_directions): 保存着RNN最后一层的输出特征。如果输入是被填充过的序列,那么输出也是被填充的序列。
-
h_n (num_layers * num_directions, batch, hidden_size): 保存着最后一个时刻隐状态。
-
-
linear:对输入数据做线性变换:\(y=Ax+b\)
参数:
- in_features - 每个输入样本的大小
- out_features - 每个输出样本的大小
- bias - 若设置为False,这层不会学习偏置。默认值:True
-
torch.unsqueeze(input, dim, out=None): 返回一个新的张量,对输入的制定位置插入维度 1
参数:
- tensor (Tensor) – 输入张量
-
dim (int) – 插入维度的索引
- out (Tensor, optional) – 结果张量
3. 模型训练
model = Net()
#MSE误差
criterion = nn.MSELoss()
#优化器
optimizer = optim.Adam(model.parameters(),lr=1e-2)
#初始化h0的值
hidden_prev = torch.zeros(1,1,hidden_size) # h0
#共训练1000次
for iter in range(3000):
#随机生成正弦函数左边界
start = np.random.randint(5) # random in [0,5]
#将序列划分为等间距的区间
x_value = np.linspace(start,start+10,x_num)
#生成训练数据
data = np.sin(x_value)
#embedding,将数据转换为100*1的矩阵
data = data.reshape(x_num,1)
#输入是0-48的数据值
x = torch.tensor(data[:49]).float().view(1,x_num-1,1)
#预测1-49的数据值
y = torch.tensor(data[1:]).float().view(1,x_num-1,1)
#训练模型
output,hidden_prev = model(x,hidden_prev)
hidden_prev = hidden_prev.detach()
#计算损失函数
loss = criterion(output,y)
model.zero_grad()
#计算与图中叶子结点有关的当前张量的梯度
loss.backward()
#优化
optimizer.step()
#输出损失函数值
if iter%100 == 0:
print('steps: {} loss {}'.format(iter,loss.item()))
note:
- 这里每次训练都要重新对该batch中的数据赋值
- detach: 返回一个新的Variable,从当前图中分离下来的。
- zero_grad(): 将module中的所有模型参数的梯度设置为0.
4. 可视化
#绘制预测图
predictions = []#预测值
input = x[:,0,:]
for _ in range(x.shape[1]):
input = input.view(1,1,1)
(pred,hidden_prev) = model(input,hidden_prev)
input = pred
#根据当前值预测下一个值
predictions.append(pred.detach().numpy().ravel()[0])
#绘制原图
x = x.data.numpy().ravel()
y = y.data.numpy()
plt.scatter(x_value[:-1],x.ravel(),s=90)
plt.plot(x_value[:-1],x.ravel())
plt.scatter(x_value[1:],predictions)
plt.show()
note:
-
numpy.ravel() 将多维数据降维,返回视图
结果:
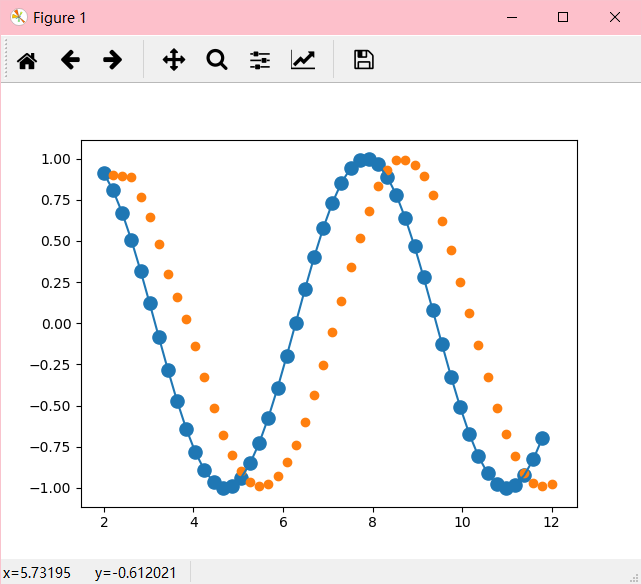
参考:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号