【ShareAi】深度学习介绍
深度学习介绍
深度学习发展历史
- 1958: Perceptron (linear model)
- 1969: Perceptron has limitation
- 1980s: Multi-layer perceptron
- Do not have significant difference from DNN today
- 1986: Backpropagation
- Usually more than 3 hidden layers is not helpful
- 1989: 1 hidden layer is “good enough”, why deep?
- 2006: RBM initialization (breakthrough)
- 2009: GPU
- 2011: Start to be popular in speech recognition
- 2012: win ILSVRC image competition 感知机(Perceptron)非常像我们的逻辑回归(Logistics Regression)只不过是没有sigmoid激活函数。09年的GPU的发展是很关键的,使用GPU矩阵运算节省了很多的时间。
深度学习三步走
深度学习与机器学习类似,同样也可以认为由三步构成
- Step1:构建神经网络
- Step2:模型评估
- Step3:选择最优函数
Step1:Neural Network
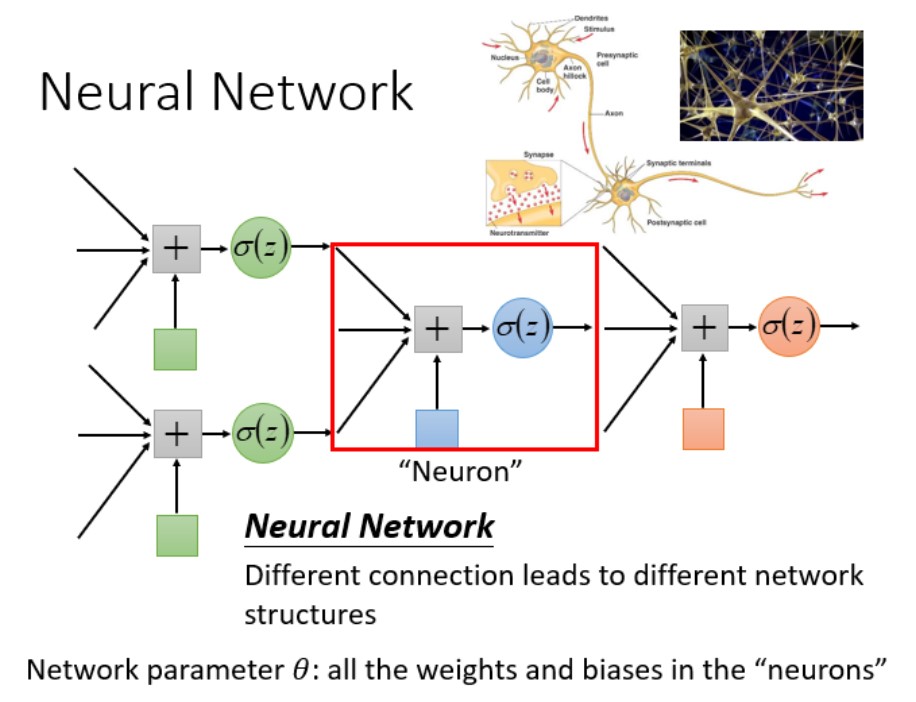
-
Fully Connect Feedforward Network
前馈神经网络,是一种最简单的神经网络,各神经元分层排列,每个神经元只与前一层的神经元相连。接收前一层的输出,并输出给下一层,各层间没有反馈
为什么叫Fully Connect?因为每层之间相互连接(Layer1和Layer2,Layer1的Output是所有Layer2的Input)
为什么叫Feedforward?因为参数传递从后往前传播
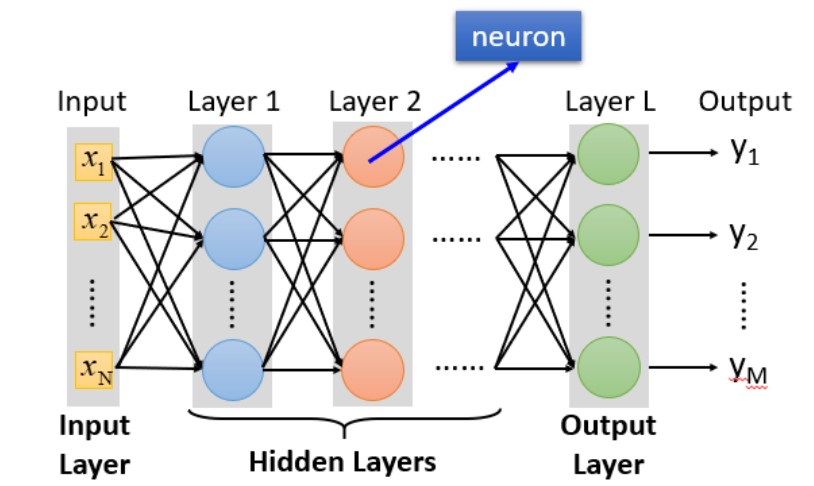
- Input Layer:1层
- Hidden Layer:N层
- Output Layer:1层
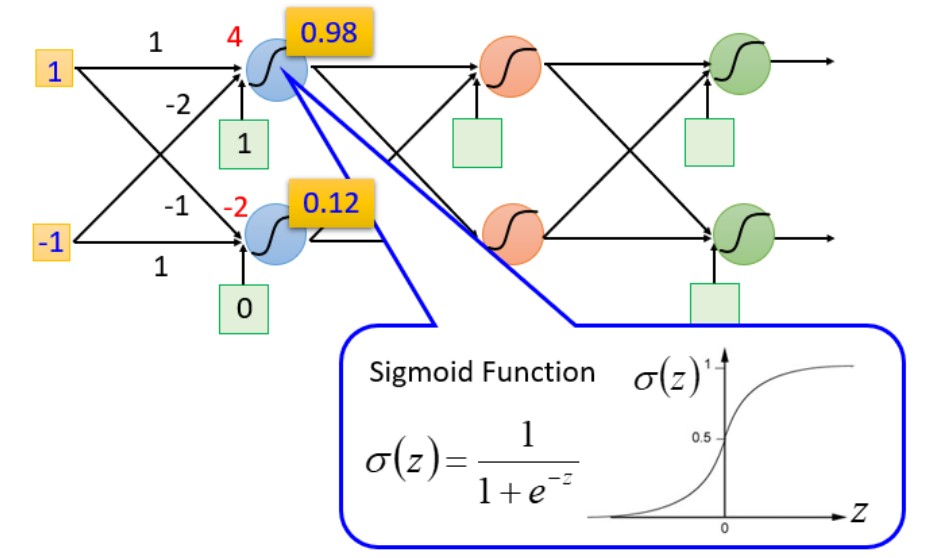
当已知输入分别为1,-1时,经过一系列复杂的运算得到结果为0.62,0.83
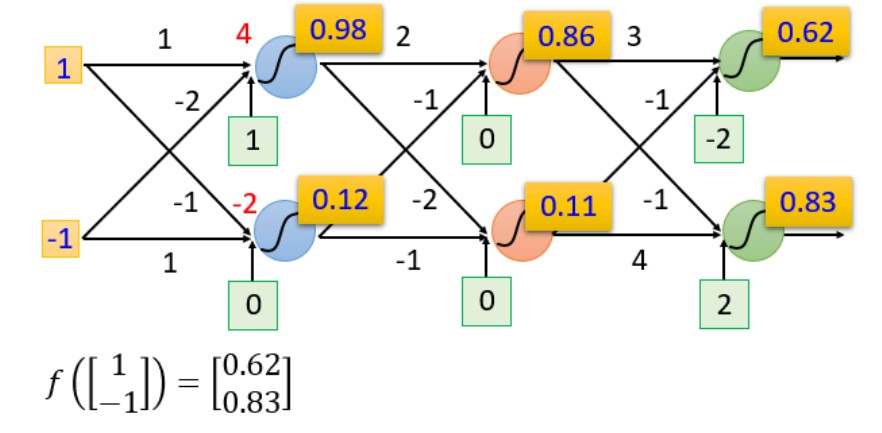
当已知输入分别为0,0时,经过一系列复杂的运算得到结果为0.51,0.85
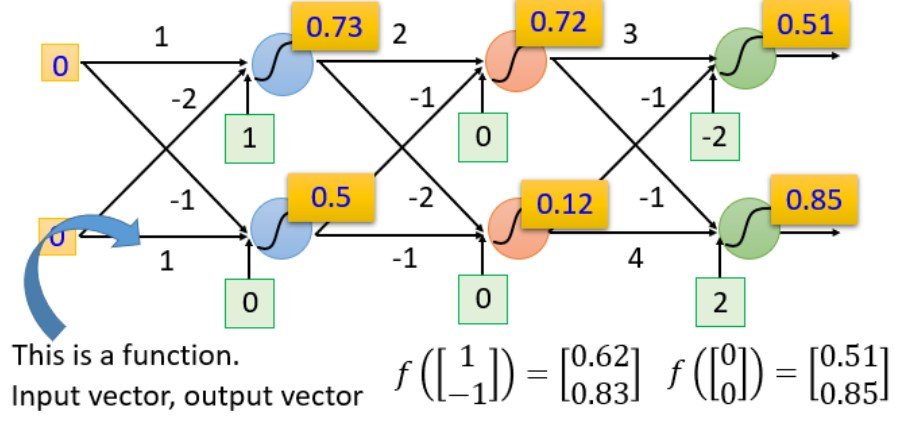
-
Deep = Many Hidden Layers
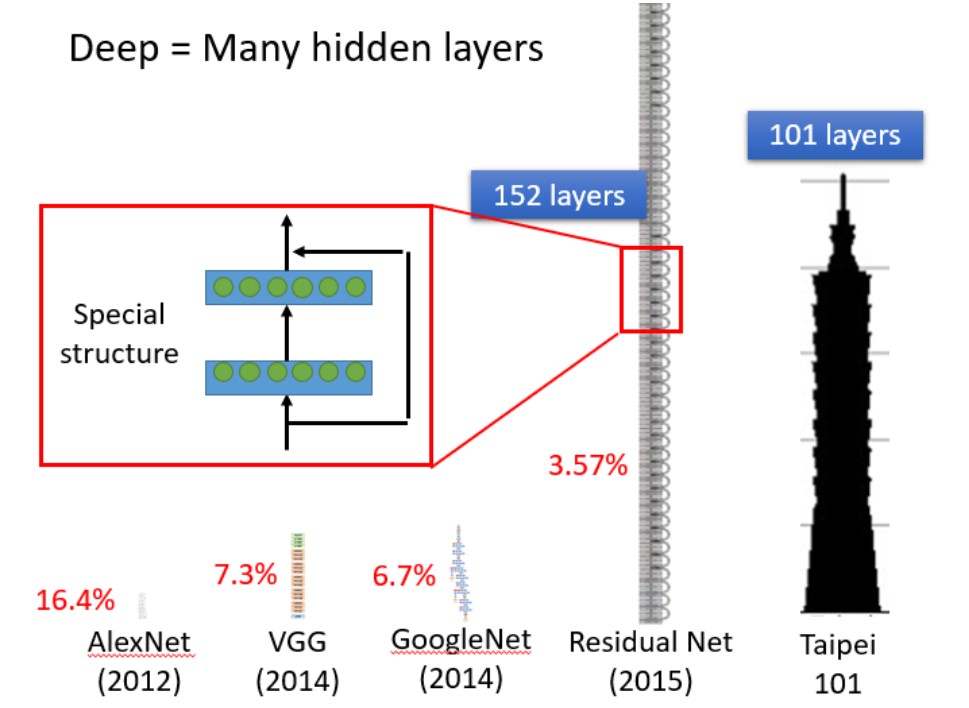
- 2012 AlexNet:8层
- 2014 VGG:19层
- 2014 GoogleNet:22层
- 2015 Residual Net:152层
- 101 Taipei:101层
随着层数变多,错误率降低,随之运算量增大,通常都是超过亿万级的计算
-
Matrix Operation(矩阵运算)
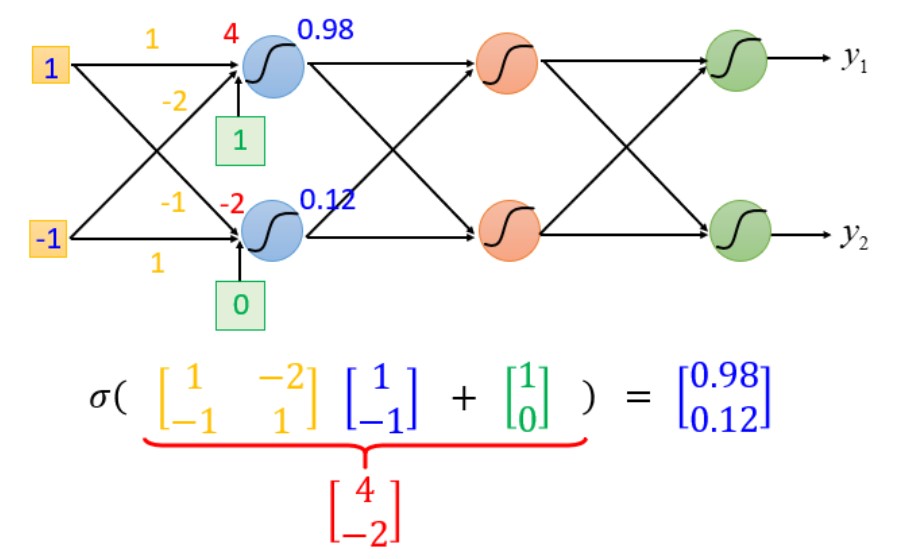
sigmoid(权重w[黄色] * 输入[蓝色]+ 偏移量b[绿色])= 输出,sigmoid一般的来说是激活函数(activation function)
Input =\(\left[ \begin{matrix} 1 \\ -1 \end{matrix} \right]\)
Ouput =\(\left[ \begin{matrix} 0.98\\ 0.12 \end{matrix} \right]\)
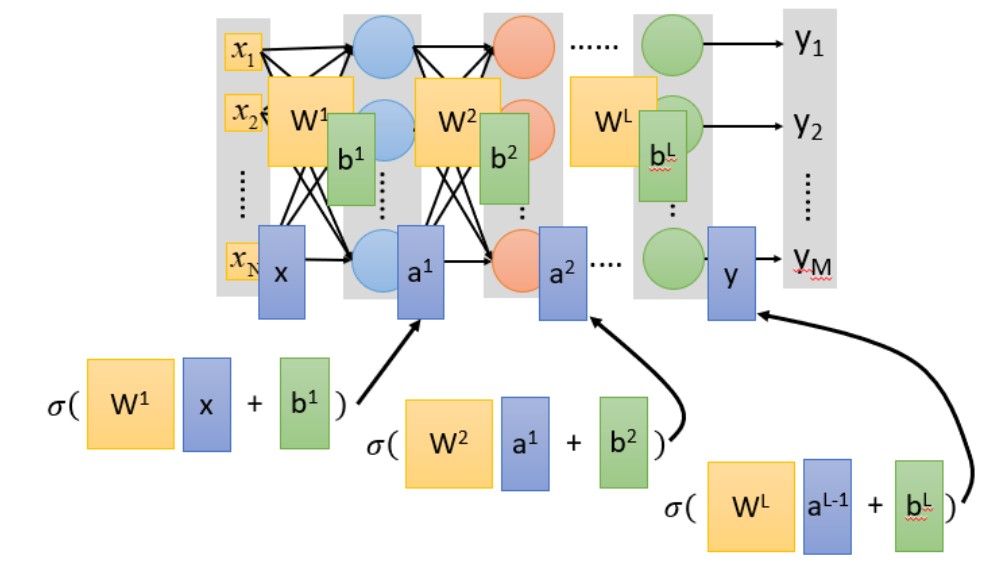
如果有N层?
\(a^1=\sigma(w^1x+b^1)\)
\(a^2=\sigma(w^2x+b^1)\)
...
\(a^n=\sigma(w^nx+b^1)\)

整个神经网络运算相当于一连串的矩阵运算,而使用矩阵运算的好处是可以使用GPU进行加速
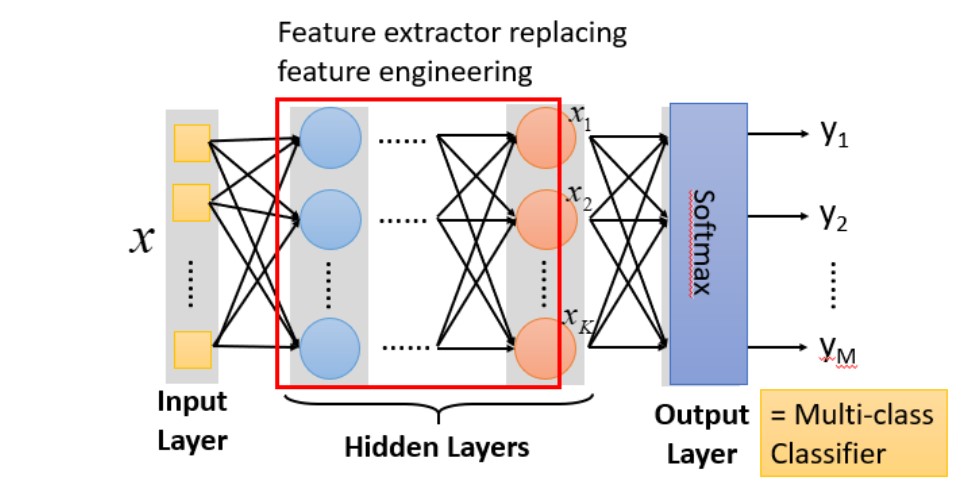
把隐藏层通过特征提取来替代原来的特征工程,这样在最后一个隐藏层输出的就是一组新的特征(相当于黑箱操作)而对于输出层,其实是把前面的隐藏层的输出当做输入(经过特征提取得到的一组最好的特征)然后通过一个多分类器(可以是softmax函数)输出最后值
几个问题?
- 多少层? 每层有多少神经元? 这个问题我们需要用尝试加上直觉的方法来进行调试。对于有些机器学习相关的问题,我们一般用特征工程来提取特征,但是对于深度学习,我们只需要设计神经网络模型来进行就可以了。对于语音识别和影像识别,深度学习是个好的方法,因为特征工程提取特征并不容易。
- 结构可以自动确定吗? 有很多设计方法可以让机器自动找到神经网络的结构的,比如进化人工神经网络(Evolutionary Artificial Neural Networks)但是这些方法并不是很普及 。
- 我们可以设计网络结构吗? 可以的,比如 CNN卷积神经网络(Convolutional Neural Network )
Step2:Goodness of Function(模型评估)
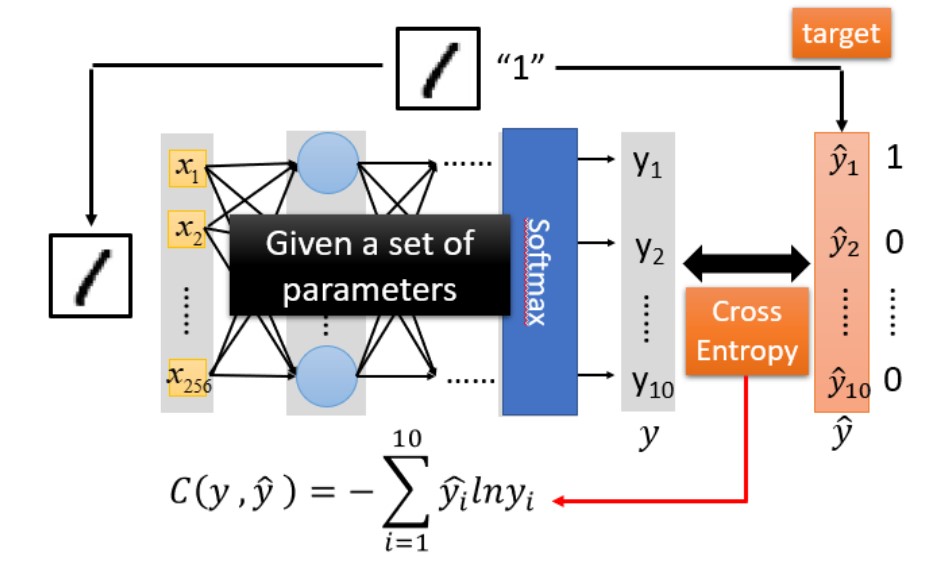
使用交叉熵(cross entropy)函数来对 y 和 \(\hat{y}\) 的损失进行计算,接下来我们就是调整参数,让交叉熵越小越好
Step3:Pick the best function
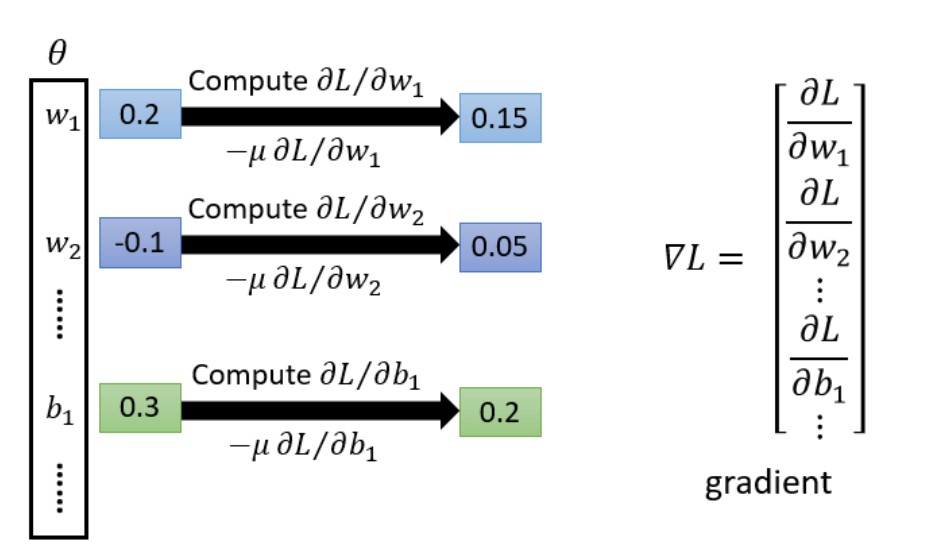
使用梯度下降法找到最优的function


