【ShareAi】机器学习 —— Where Error does come from?
Where Error does come from?

Error主要是由bias偏置和variance方差形成,可以理解为Error=bias+variance
- Error:反映模型的准确度
- Bias:反映模型在样本上的输出与真实值之间的误差,即模型本身的精准度
- Variance:反映模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性
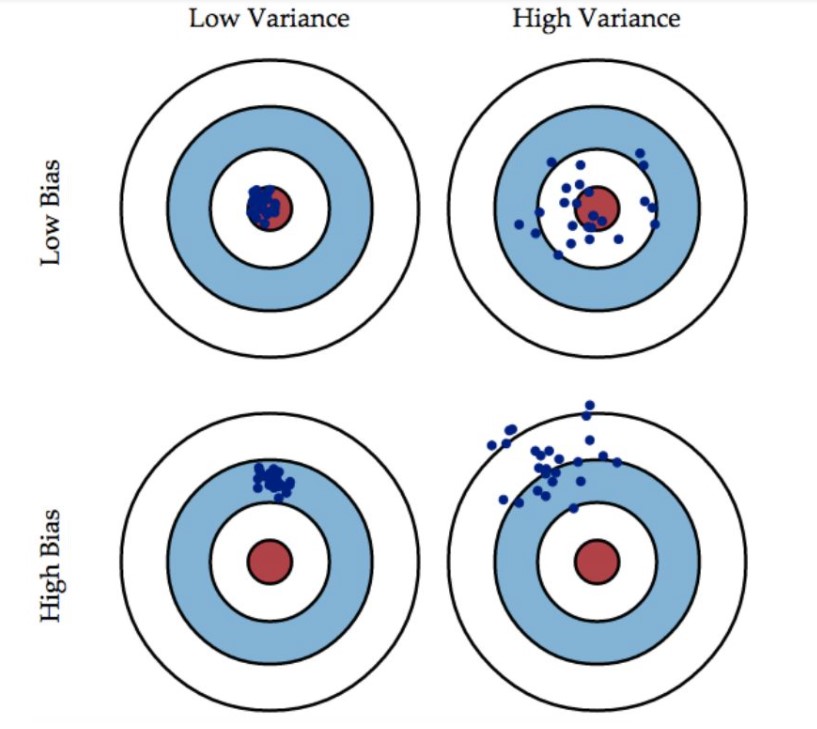
根据上图可以看出,以打靶为例,bias描述精准度,当bias较小时,说明该射击手基本打在靶心附近,精确度很高,当bias较大时则说明靶点可能偏离靶心,即射击手所获得环数较小;Variance描述稳定性,当Variance值较小时,说明打出的所有点聚集在一起,反之则分散开来,呈零散状态
评估bias和Variance
-
Estimate the mean of a variable x
- 定义x的均值为\(\mu\),x的方差为\(\sigma^2\)
-
接下来如何评估均值\(\mu\) ?
-
首先我们进行采样N个点:{\(x^1, x^2, x^3, ..., x^N\)}
-
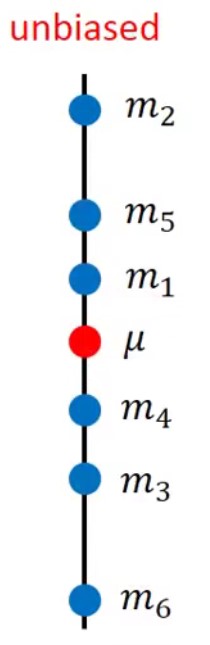
然后计算平均值m:m=\(\frac{1}{N}\sum_nx_n\),需要注意的是m \(\neq\) \(\mu\),因为只采样N个点而不是无穷多个
-
接下来计算期望值:E[m] = \(\frac{1}{N}\sum_nE[x_n] = \mu\)
-
m分布对于\(\mu\)的离散程度(方差):Var[m] = \(\frac{\sigma^2}{N}\)
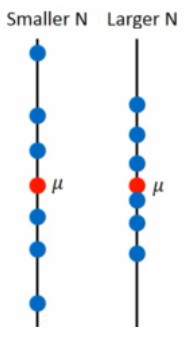
由此可见,\(\mu\)的离散程度(方差)取决于N,N越小越离散
-
-
如何评估方差\(\sigma^2\)
-
同样地,我们进行采样N个点:{\(x^1, x^2, x^3, ..., x^N\)}
-
平均值:m=\(\frac{1}{N}\sum_nx_n\)
-
\(\sigma^2\)的估测值:\(s^2 = \frac{1}{N}\sum_n(x^n-m)^2\)
-
\(s^2\)的期望值:E[\(s^2\)] = \(\frac{N-1}{N}\sigma^2 \neq \sigma^2\)
-
Variance
每次不同实验数据集在同一个Model获得的Function可能不一样
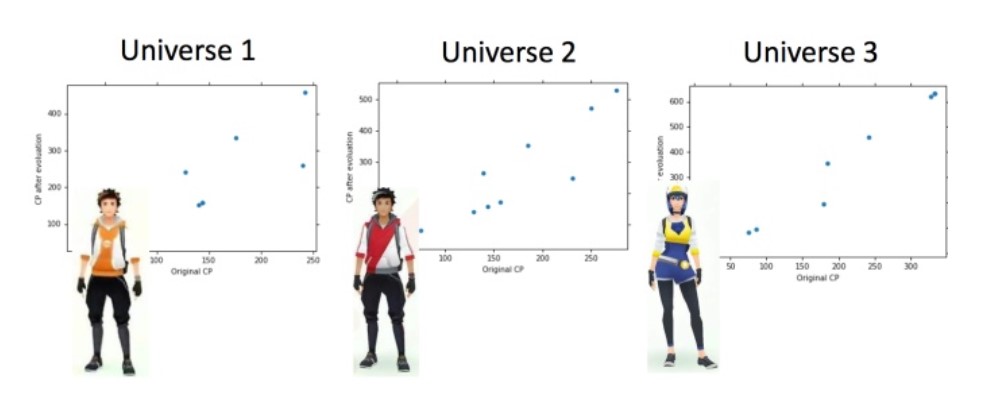
假设在Parallel Universes中,抓到不同的神奇宝贝
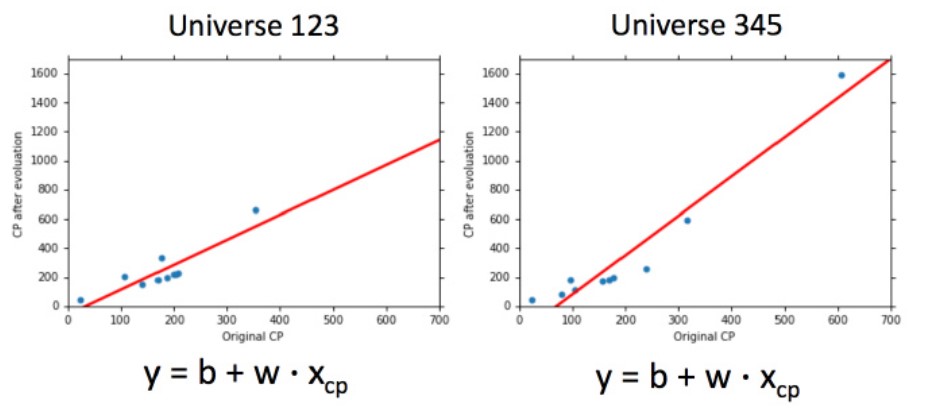
我们可以看到,在Universe123和Universe345的function是不一样的,即不同training data上\(f^*\)是不同的
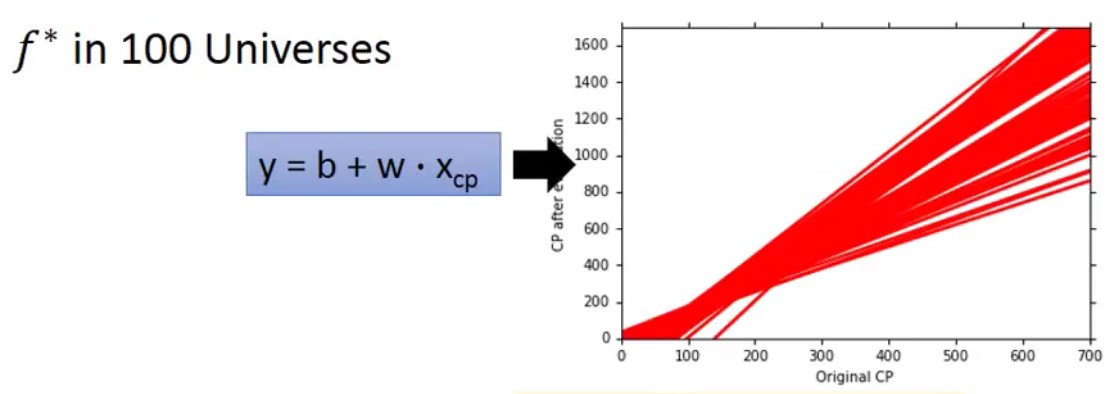
假如我们有100个Parallel Universes(使用100个不同训练集做实验),那会是怎么样呢?
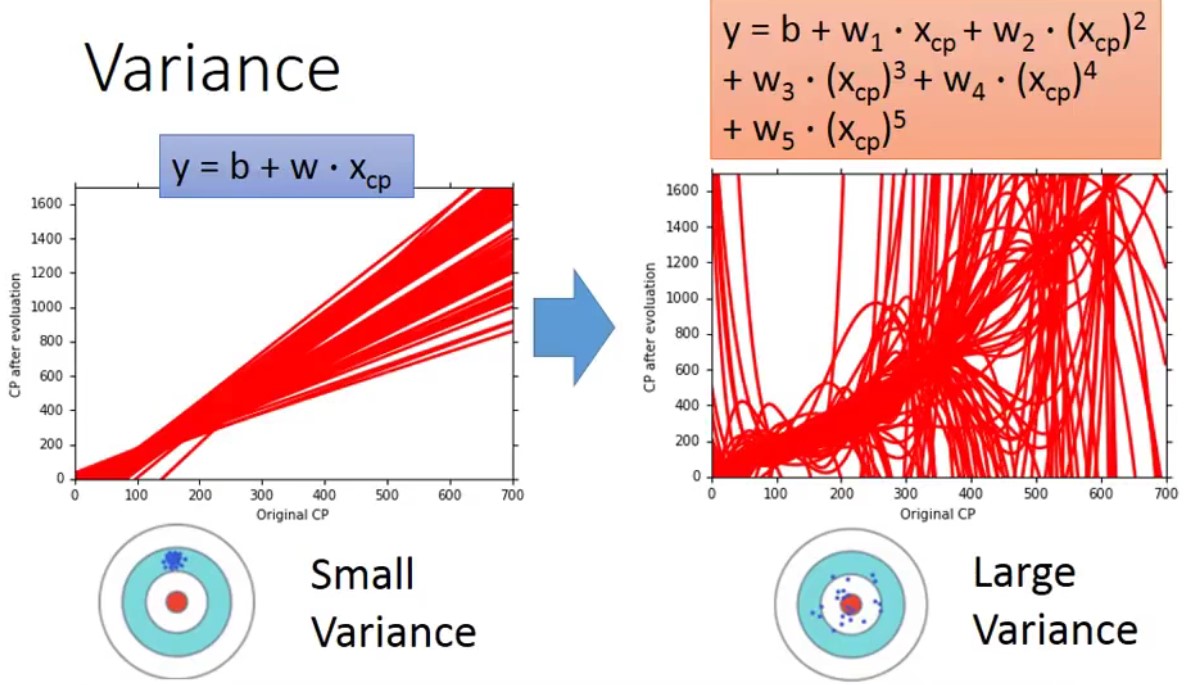
使用比较简单的Model时,Variance值是比较小;但随着模型变得越来越复杂,比如function为一元五次方程时,其Variance值变大。即简单Model受到不同的数据集的影响比较小
Bias
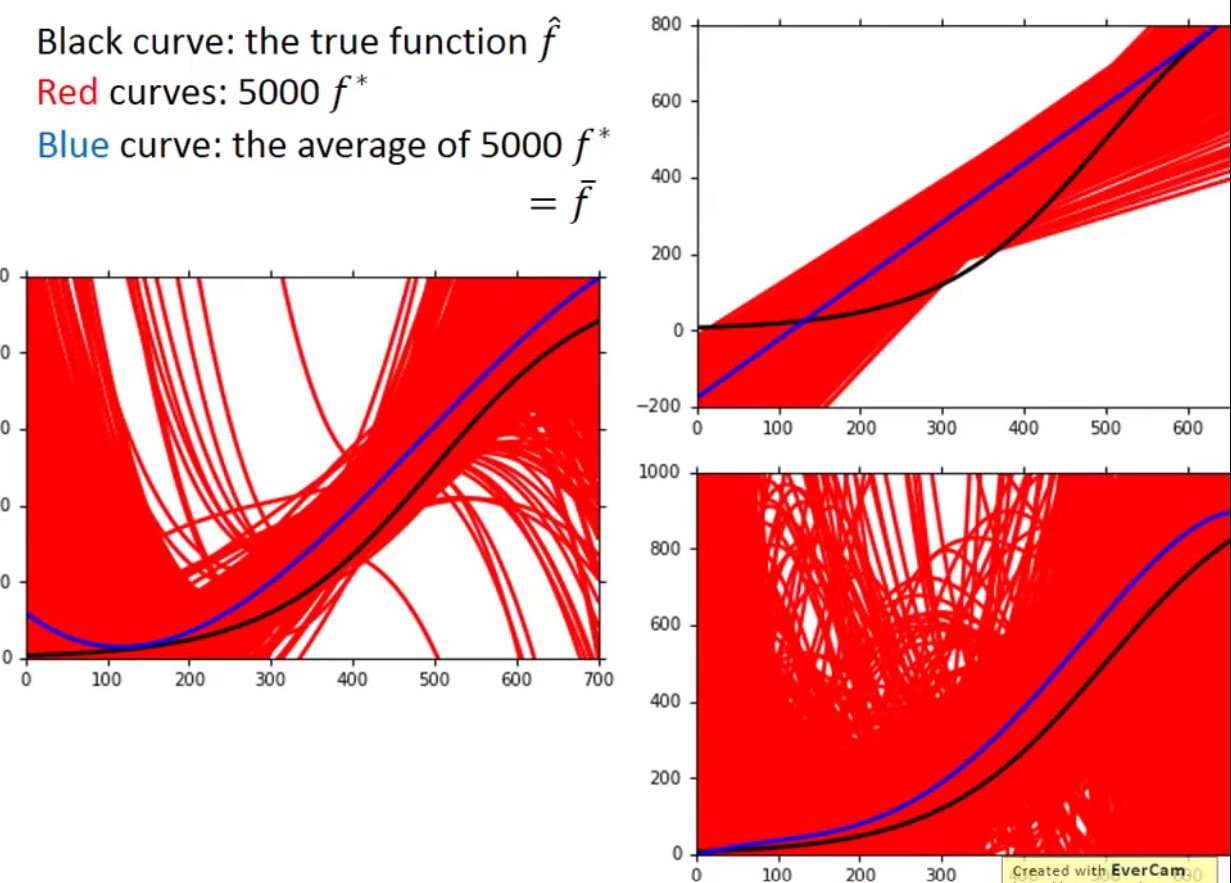
简单Model的bias比较大,而复杂Model的bias则比较小。一个Model包含很多function,而简单model的space小,可能其并没有包含target,若从数据集中sample,平均起来不可能接近target;复杂model的space大,可能包含target,则其平均值在target附近
Bias VS Variance
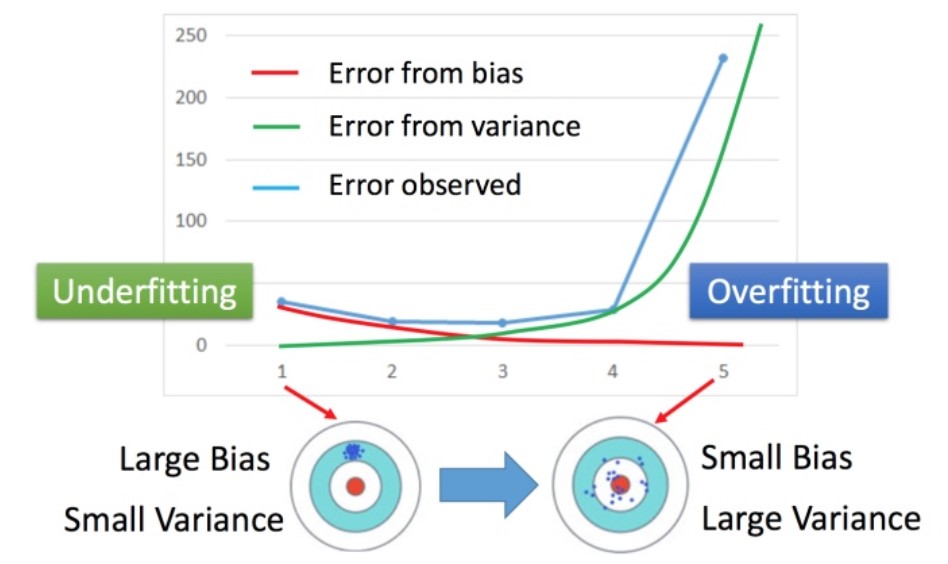
由图可以看出,比较简单model的bias比较大而variance值比较小,复杂model的bias比较小而variance值比较大且其值变化比bias要大
Error = Bias + Variance
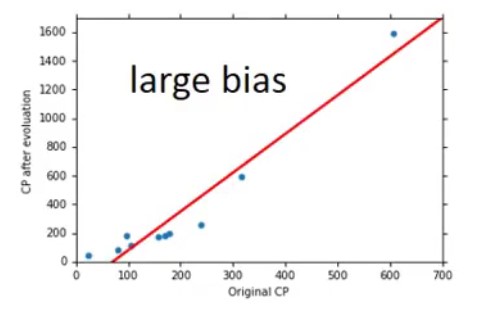
Underfitting(欠拟合):bias比较大
- 可以用更多特征作为输入
- 构建更复杂的模型
Overfitting(过拟合):variance比较大
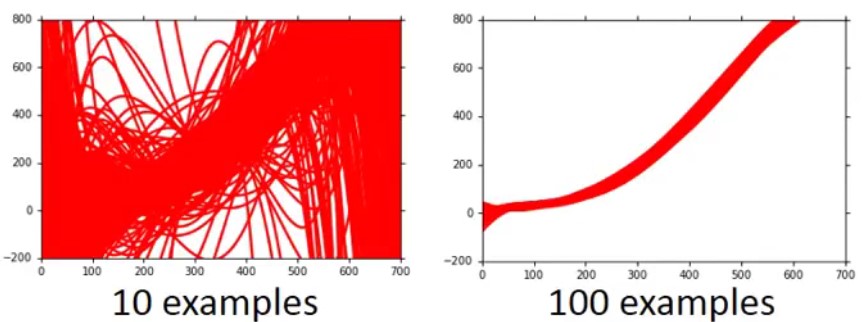
- 增加数据集
- 引入正则化处理
模型选择
在bias和variance之间平衡值大小,以选择最好的model,使得error可以达到最小值
交叉验证
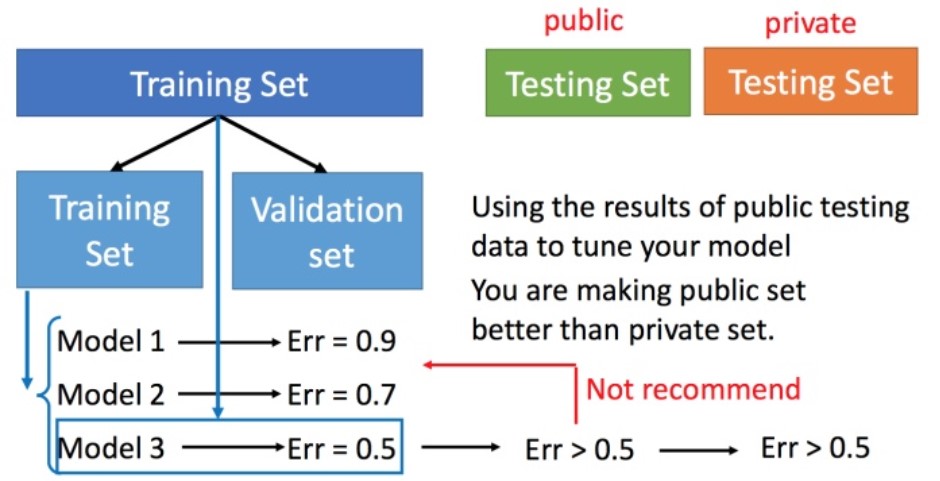
将训练集以一定比例划分为训练集和验证集,使用训练集训练模型,然后用验证集比较模型的性能指标,选出较好的一个模型,再用原所有训练集训练该模型,最后使用测试集对模型进行测试
N折交叉验证
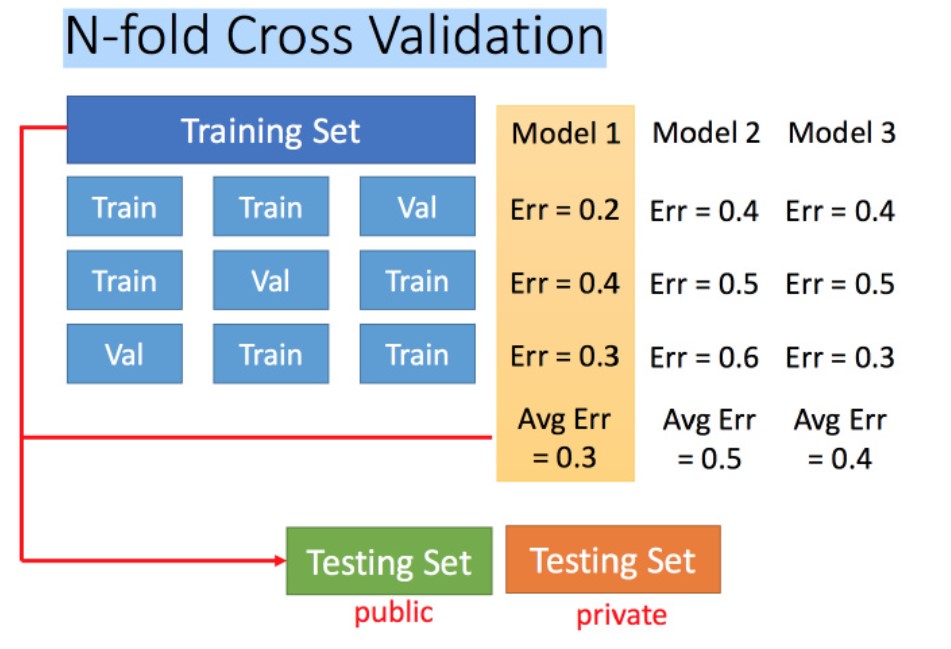
- 假设三折交叉验证,将训练集分成3份,其中两份作为训练集,一份作验证集,用来训练所有model,得到每个model的误差(性能指标)
- 然后交换训练集和验证集,继续训练和验证model,待训练完后求解每个model的平均error,选择误差最小的作为较好的model,然后再使用所有训练集训练该model
- 最后再将model用于测试集的测试中


