【ShareAi】机器学习 —— 回归Regression

机器学习 —— 回归Regression

Stock Market Forecast（股票市场预测）

• Input：过去十年股票起伏信息、股票相关公司的并购资料

• Output：预测未来股票市场指数平均值（Dow Jones Industrial Average）

Self-driving Car（无人驾驶）

• Input：汽车各种传感器所采集的数据，如超声波距离传感器、激光雷达、图像摄像头等

• Output：方向盘角度或者目前车辆行驶速度

Recommendation（推荐系统）

• Input：使用者A的购买习惯，商品B的特性

• Output：使用者A购买商品B的可能性

预测Pokeman的CP(Combat Power)指标

• Input：进化前的CP值、HP、Type、Weight、Height等特性

• Output：进化后的CP值

模型步骤（以预测Pokeman的CP指标为例）

• Step1：模型搭建（线性模型 y=w*x+b，w为权重，b为偏置）

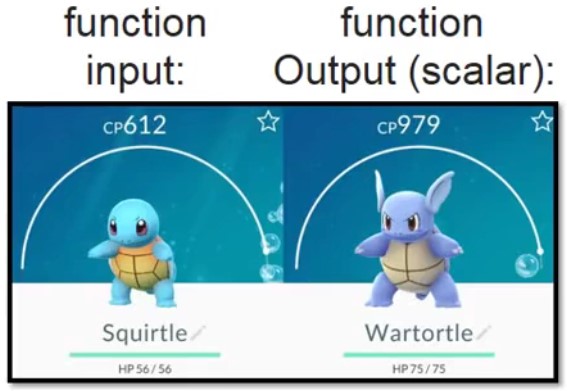
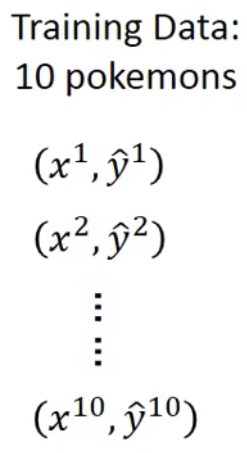
Training Data：x表示原始CP值，y表示进化后CP值

• Step2：模型Function评估（Loss Function）

  

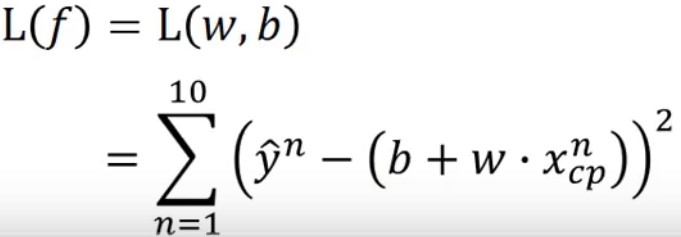
  Loss Function：input为某一个function，output为该function的好坏

• Step3：Best Function（从Function set中选出最好的一个Function，即选择损失函数值最小）

如何找出Best Function？Gradient Descent

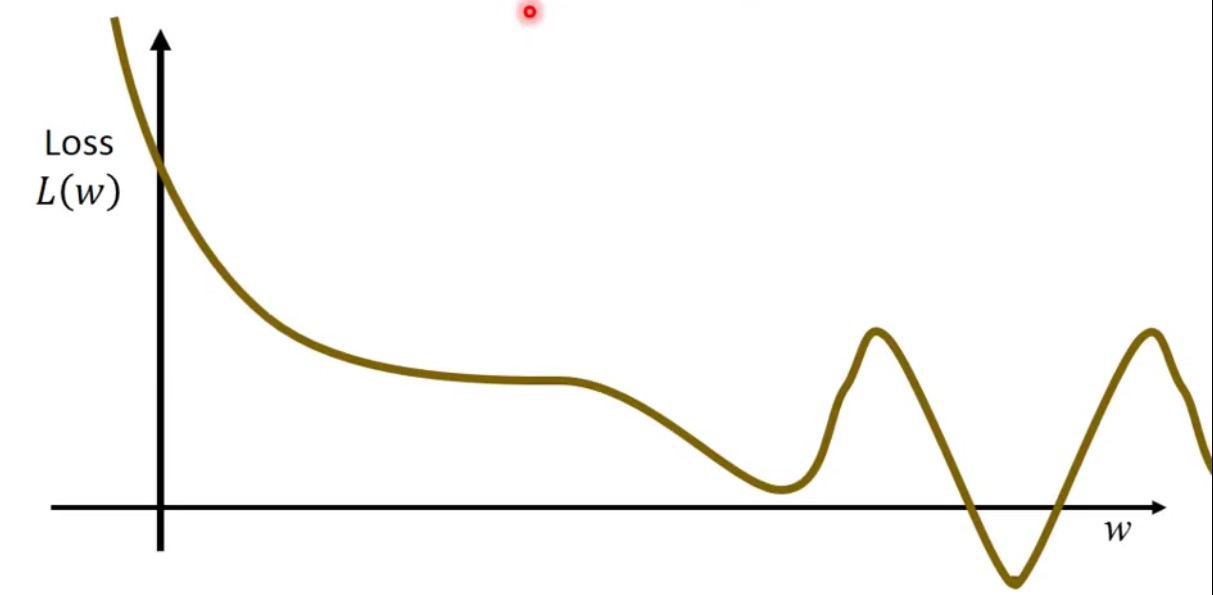
• 穷举法：遍历曲线所有值，找到L(w)最小值即为最优解（效率非常低）

• 梯度下降：

  • Step1：随机选取一个初始值\(w_0\)
  • Step2：求解w=\(w_0\)时Loss的微分
    • 当斜率为负值时，w向右增大值
    • 当斜率为正值时，w向左减小值
  • Step3：设置学习率(Learning Rate)
  • 不断重复执行Step2和Step3，直到找到最小值（局部最小值）

• 梯度下降法图演示过程

  
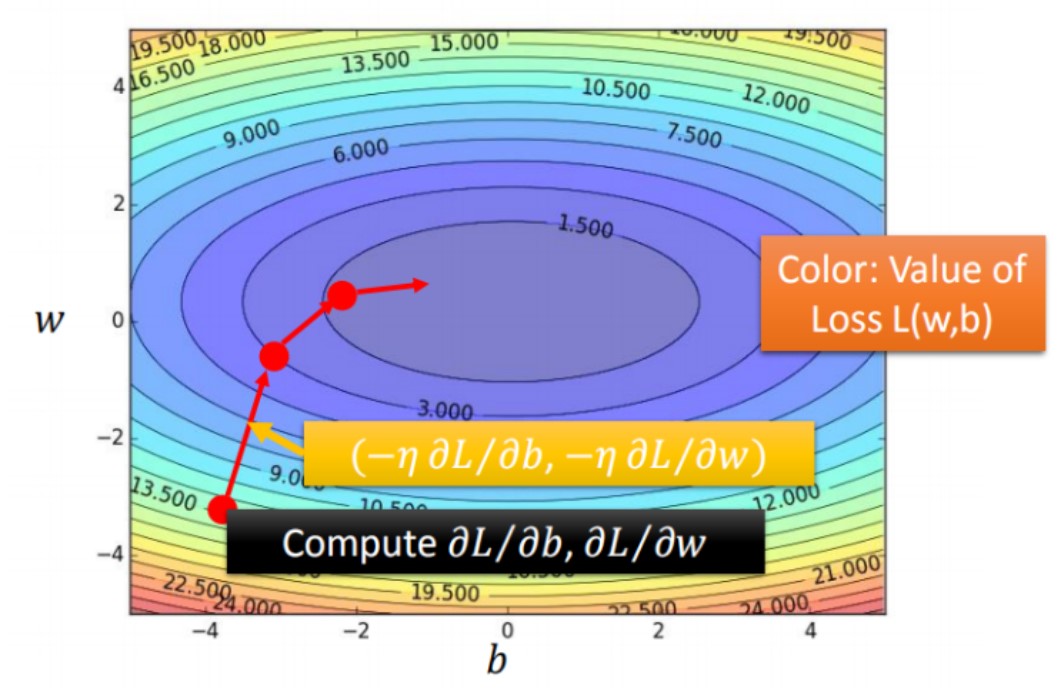
  • 图中等高线对应每个Loss值，由外往里值越来越小
  • 红色箭头为对应位置等高线的法线方向

训练结果如何？

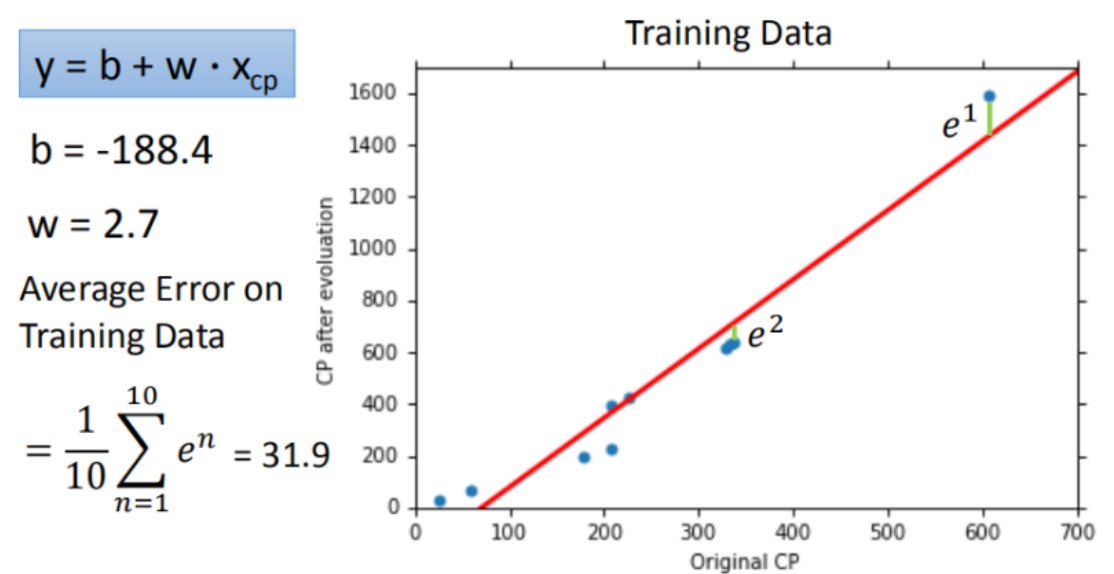
计算训练数据集的平均误差来验证模型好坏，该模型在training data的平均误差为31.9

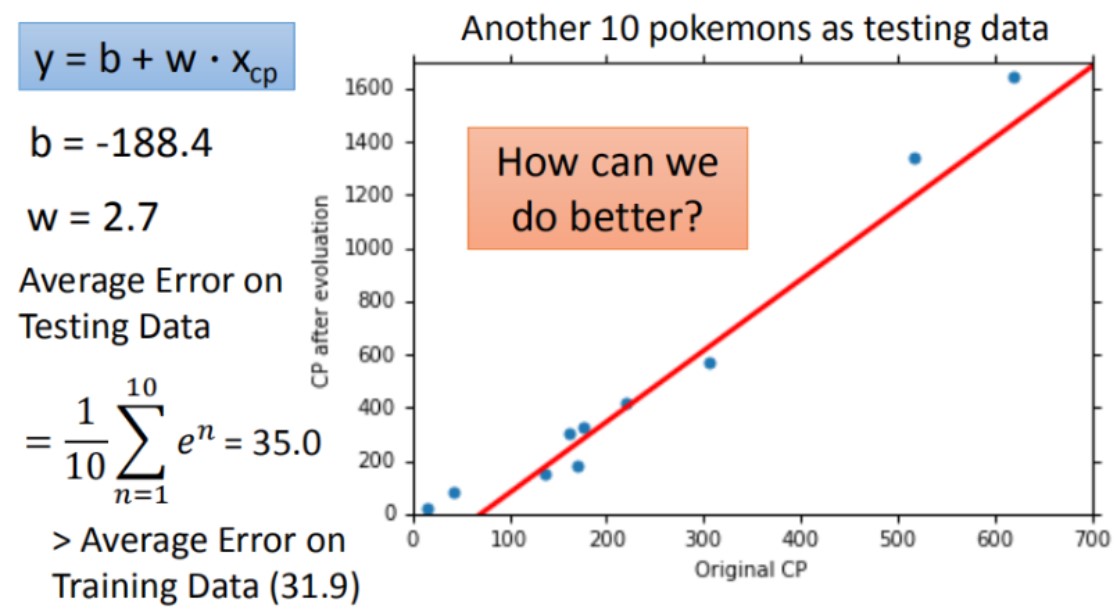
计算测试数据集的平均误差来验证模型好坏，该模型在testing data的平均误差为35.0

因为best function是在training data上找到的，所以在testing data的平均误差要比在训练数据集的平均误差大一点

引入更复杂的模型：一元N次线性模型

一元二次线性方程：y = b + \(w_1\)\(x_1\) + \(w_2\)(\(x_2\))²

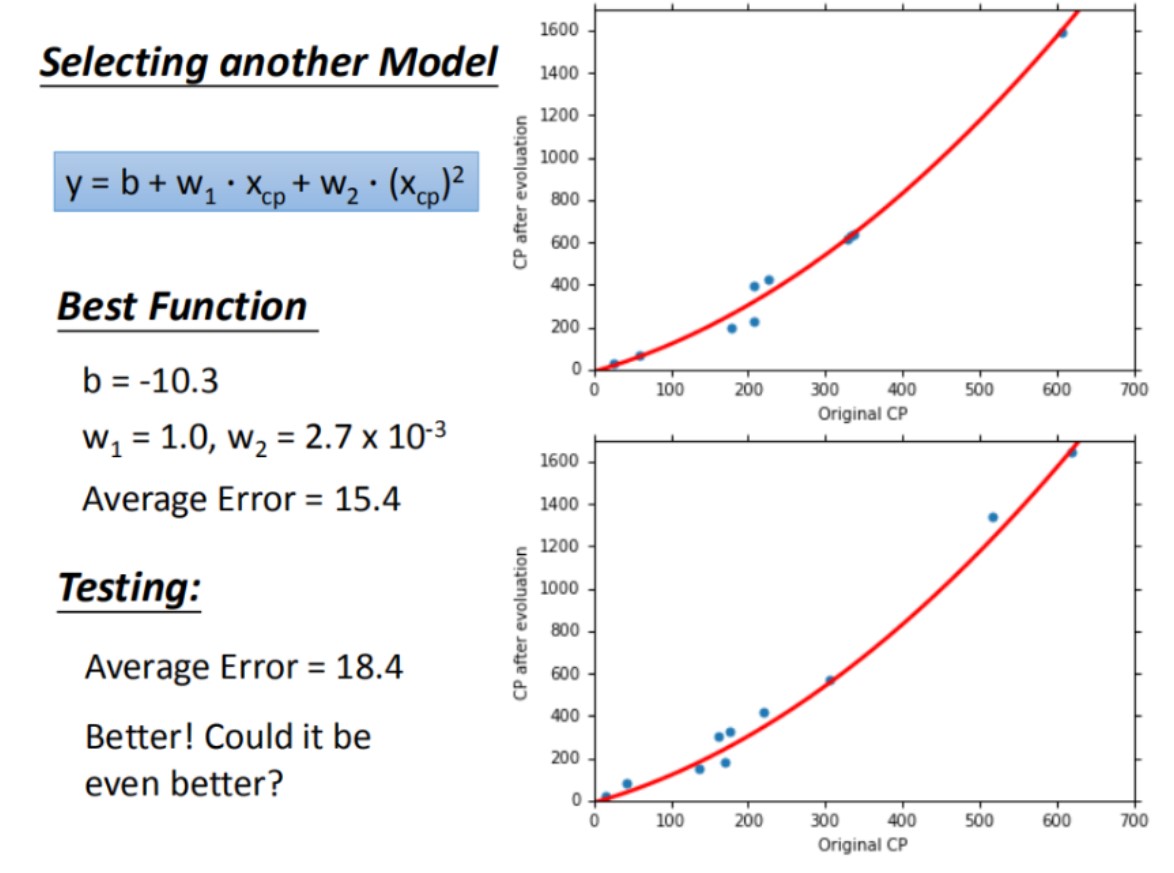
training data的平均误差为15.4，testing data 的平均误差为18.4

过拟合问题

拟合问题判断标准

训练集表现	测试集表现	结论
好	不好	过拟合
不好	不好	欠拟合

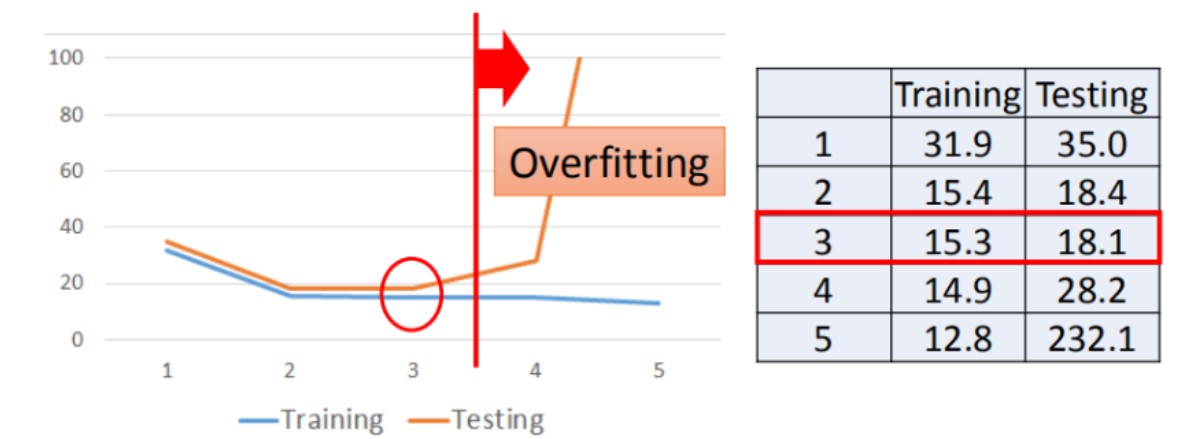
数据集在不同一元N次线性方程中的平均误差（分别为一次、二次、三次、四次、五次）

training data的平均误差：31.9、15.4、15.3、14.9、12.8

testing data 的平均误差：35.0、18.4、18.1、28.8、232.1

可以看到，当使用更高次方（更复杂）的模型时，在训练集上的表现越来越优秀，但在测试集上的效果却越来越差，这就是出现了过拟合问题

说明，越复杂的模型在training data上可以有比较好的结果，但在testing data上并不总是可以带来更好的表现

步骤优化

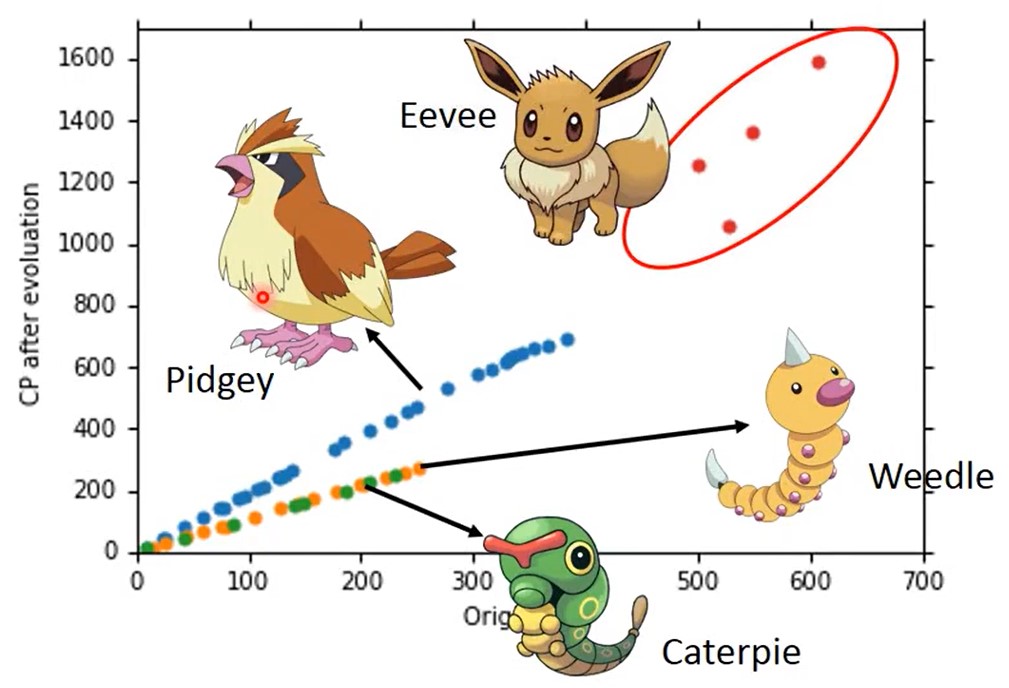
当我们数据集足够大时，我们发现更深的特征，不同种类Pokemon在进化前是相同CP值，但进化后CP值甚至可以相差2倍，即不同Pokemon种类会影响其进化后CP值的结果

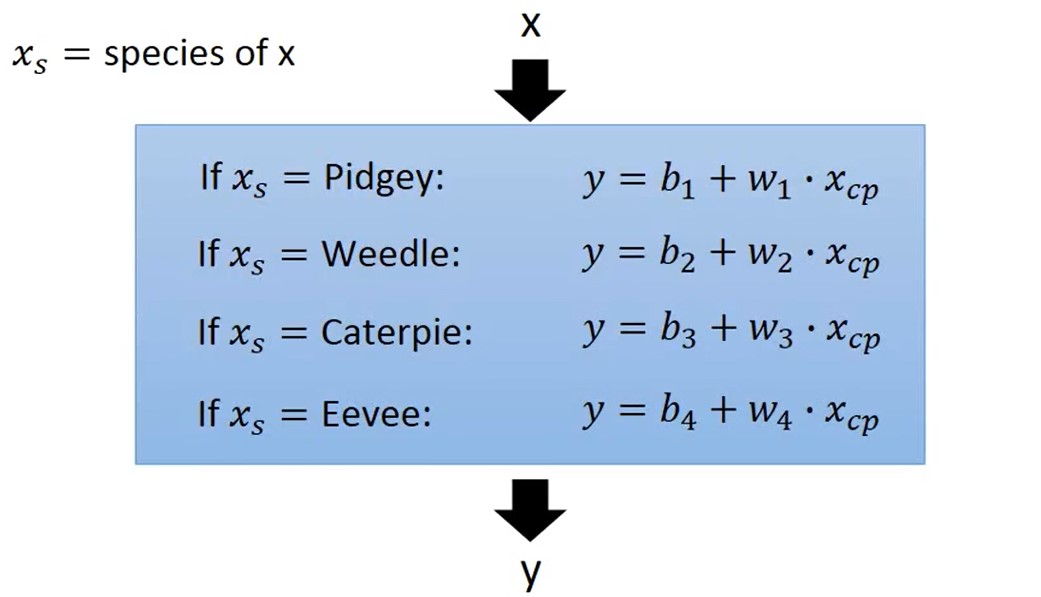
• Back to Step1：重新设计Model的Function

  • 每个物种都有一个function，而且每个function的w权重和b偏置值都不一样

  • 我们将每个物种对应的function合并为一个function线性方程，即y = b + \(\sum\)\(w_i\)\(x_i\)

    

  • 通过以上图，我们发现使用新模型，training data和testing data的平均误差值都有一定程度的下降

  

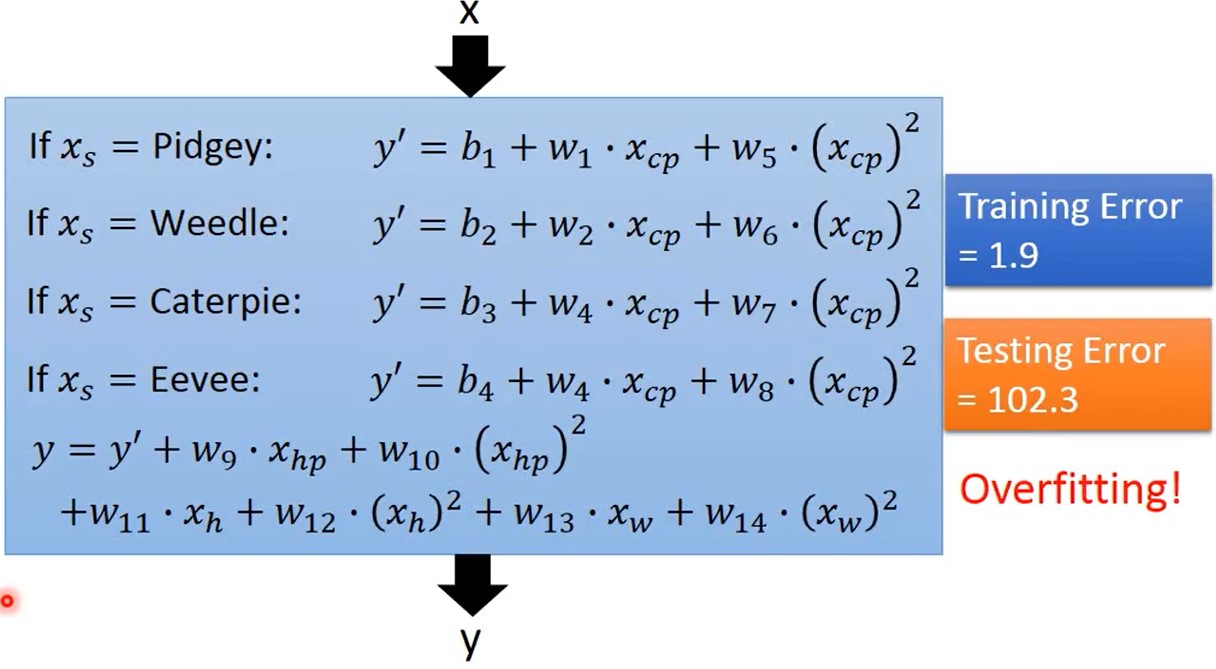
• Back to Step1：引入更多维度的参数（Height、Weight、HP等）

  • 通过实验可以发现，引入多个特征值后，模型出现过拟合现象

• Back to Step2：Regularization（归一化），可能会以增大训练误差为代价来减小测试误差，以达到去过拟合效果

  
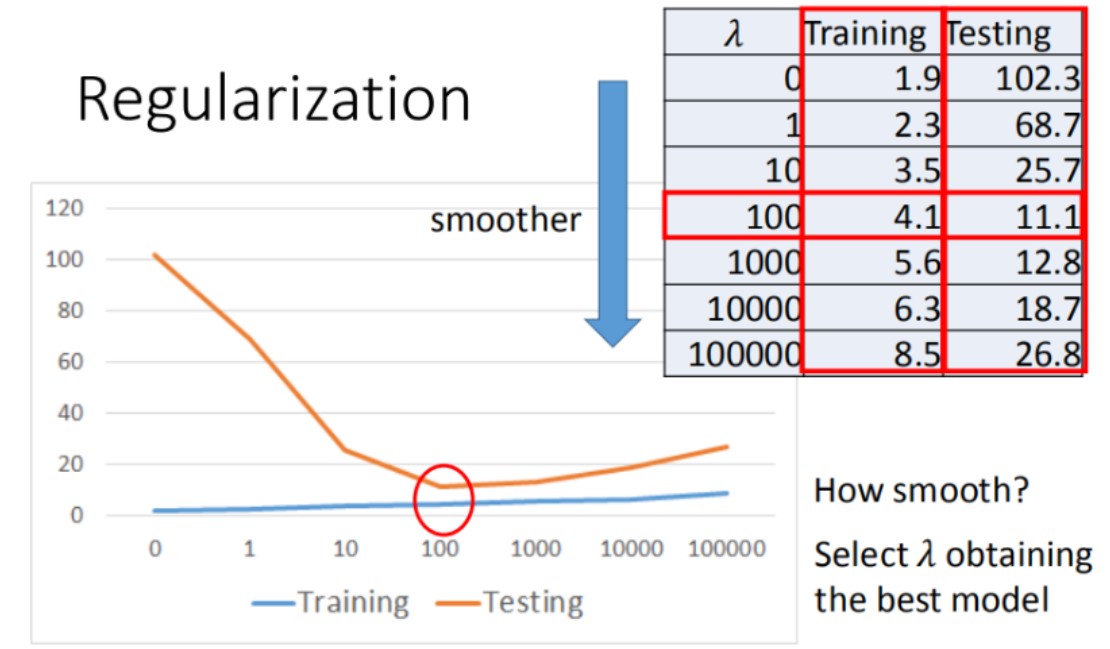
  • 保留所有的特征变量，但会减小特征变量的数量级