傅里叶系列（三）离散傅里叶变换（DFT）

转载：https://zhuanlan.zhihu.com/p/75521342

我们将傅里叶级数推导为傅里叶变换，而傅里叶变换计算的时候因为是一个积分，计算机并不是很好计算，所以要把积分换成一种累加形式，也就是本文要讨论的 离散傅里叶变化 DFT。

我们取上一篇的公式（7）

其中

因为傅里叶变化令  从而使一个累加的式子变成了一个积分，而DFT中  会根据输入的信号点数确定具体的值。具体计算公式为：

(注：  的计算方式是因为 的一个周期是  ,N为你采样的点数)

因此我们可以简化公式为

因为标准化的傅里叶变化  有：

其中：

其中(1)为离散傅里叶逆变换,(2)为离散傅里叶变化。

代码实现：

先定义一个复数的结构体

public struct complex//定义复数  
{
    public double real;
    public double imag;

    // 写个函数用于显示
    public void show()
    {
        if (Math.Abs(real) < 0.0001) real = 0;
        if (Math.Abs(imag) < 0.0001) imag = 0;
        if (imag > 0) Debug.Log(string.Format("{0} +{1}i", real, imag));
        else if (imag == 0) Debug.Log(string.Format("{0}", real));
        else Debug.Log(string.Format("{0} {1}i", real, imag));
    }
}

注:t为f数组的索引，n为F数组的索引，理清楚了代码很好理解

计算DFT,即已知一个 float 数组求频谱

public static complex[] calDFT(double[] f)  //(信号，信号长度)   
{
    int N = f.Length;
    complex[] F = new complex[N];
    for (int n = 0; n < N; n++)
    {
        // 声明
        F[n].real = 0;
        F[n].imag = 0;
        for (int t = 0; t < N; t++)
        {
            // 计算 exp(-i * 2PI * n / N * t)
            complex temp;
            // 欧拉公式 exp(ix) = cos(x) + isin(x)
            temp.real = Math.Cos(-2 * Math.PI / N * t * n) * f[t];
            temp.imag = Math.Sin(-2 * Math.PI / N * t * n) * f[t];

            F[n].real = F[n].real + temp.real;
            F[n].imag = F[n].imag + temp.imag;
        }
    }
    return F;
}

计算IDFT,即已知一个 float 数组求频谱

public static complex[] calIDFT(complex[] F)  //(频谱)   
{
    int N = F.Length;
    complex[] f = new complex[N];
    for (int t = 0; t < N; t++)
    {
        // 声明
        f[t].real = 0;
        f[t].imag = 0;
        for (int n = 0; n < N; n++)
        {
            // 计算 exp(i * 2PI * n / N * t)
            complex temp;
            // 欧拉公式 exp(ix) = cos(x) + isin(x)
            double real = Math.Cos(2 * Math.PI * n / N * t);
            double imag = Math.Sin(2 * Math.PI * n / N * t);
            // 复数乘法
            temp.real = F[n].real * real - F[n].imag * imag;
            temp.imag = F[n].real * imag + F[n].imag * real;

            f[t].real = f[t].real + temp.real;
            f[t].imag = f[t].imag + temp.imag;
        }
        f[t].real = f[t].real / N;
        f[t].imag = f[t].imag / N;
    }
    return f;
}

随便输入一个float的数组做一下实验

double[] signal = new double[] { 14,12,10,8,6,10};
Debug.Log("----------计算离散傅里叶变化-------------");
var rate = calDFT(signal);
foreach (var item in rate)
{
    item.show();
}
Debug.Log("----------计算反离散傅里叶变化------------");
var irate = calIDFT(rate);
foreach (var item in irate)
{
    item.show();
}

结果如下：

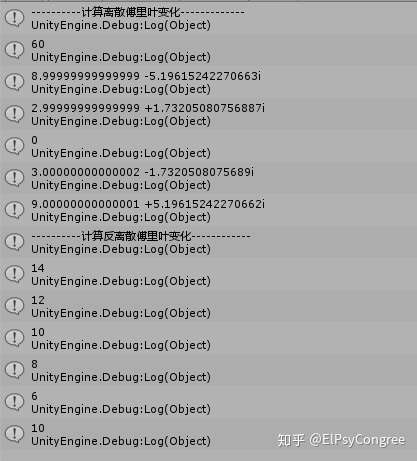
学过线性代数的会觉得有点像是 某个 维数很高的向量乘以 一个对应的矩阵，然后在乘以一个逆矩阵...转回来的过程。

我们记 

得到DFT的矩阵：

以及IDFT的矩阵：