支持向量机SVM、优化问题、核函数
1、介绍
它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
2、求解过程
1、数据分类—SVM引入
假设在一个二维平面中有若干数据点(x,y),其被分为2组,假设这些数据线性可分,则需要找到一条直线将这两组数据分开。这个将两种数据分割开的直线被称作分隔超平面(separating hyperplane),当其在更加高维的空间中为超平面,在当前的二维平面为一条直线。
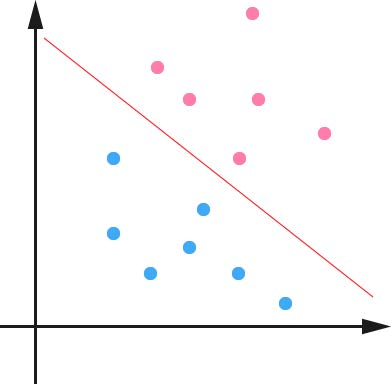
这样的直线可能存在很多条,则我们需要找到一条最优的直线。怎么定义这个最优直线呢?如果依此构建的分类器能够在测试结果将测试数据分开,且数据点离这一决策边界越远,其结果将更可信。那么在该二维平面中,需要使得离分割超平面最近的点,其离分割面尽可能远。
设这些点到分割面的距离用间隔(margin)表示,则我们需要最大化这些间隔,从而使得最后得到的分类器在测试数据上表现地更加健壮。
那么,什么是支持向量(support vector)呢?就是离分割超平面最近的那些点。在超平面两侧最近的点形成了间隔边界,而超平面则处于这两个间隔边界的中心。
2、找到最大间隔
以二维平面为例。
在二维平面中的分割超平面为一条直线,我们将其表示为:
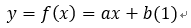
其也可以表示为:
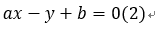
我们可以把x,y看成在这二维平面上的某个数据点的两个特征,那么这个二维平面也就是特征空间。这样,重新定义其特征为x1,x2 ,对应系数为w1,w2,对于更高维次,则有xn,wn,于是我们可以把特征及其系数表示为WTX,其中W、X都是n维列向量。此时该超平面可表示为:
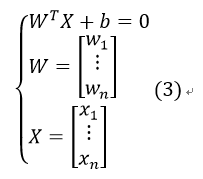
那么如何刻画两个不同的分类呢?我们设:
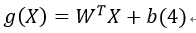
上式表示刻画n维特征的数据的分类函数。显然,如果g(X)=0,则在超平面上;其余数据将被该超平面分为2部分,不妨设使得g(X)>0的数据类别为1,g(X)<0的数据类别为-1.
函数间隔(函数距离)
我们定义函数间隔如下:
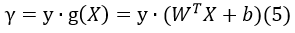
在超平面WTX+b=0确定的情况下,|WTX+b|可以能够相对的表示数据X距离超平面的远近。而WTX+b的符号与类标记y的符号是否一致表示分类是否正确。所以,γ的值越大,表示分类正确且距离超平面越远,该模型越可信。(当γ的值>0时,即可表示对应的数据点分类正确)
因此,我们需要最大化最小间隔,设m为数据点个数:
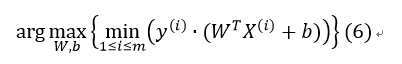
但是,这里存在一个问题,即当W和b成比例的缩放时,超平面并没有改变,但是函数间隔γ的取值也扩大2倍,意指通过最大化函数间隔没有意义,因为任何成功划分训练实例的超平面都可以使函数间隔无限大。
接下来我们将引入几何间隔。
几何间隔
定义几何间隔如下:
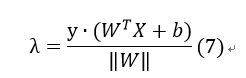
此处y·(WTX+b)其实就相当于|y·(WTX+b)|(当该数据点被正确分类时)。其中||W||为L2范数:
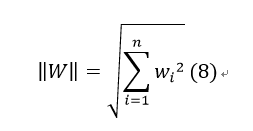
其实,几何间隔所描述的其实就是点到超平面的垂直距离。比如对于二维平面中ax+by+c=0这一直线,直线外一点(x1,y1)到该直线的距离为:
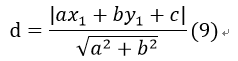
而7式只是将其扩展至高维平面。由此定义的需要的求解目标为:
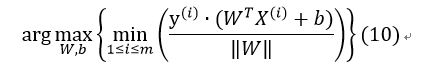
也可以设最小几何间隔为δ,变为以下形式:
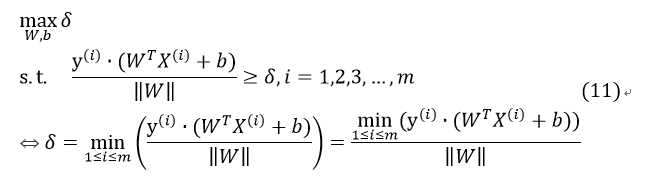
其中2式和3式表达的意思相同。上式中的第三个式子等号成立的原因在于:
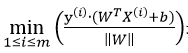 表示在m个数据点中找几何间隔最小的,此时与
表示在m个数据点中找几何间隔最小的,此时与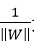 无关,可将其提出表达式。
无关,可将其提出表达式。
因为几何间隔与函数间隔差一个||W||的系数,可以设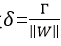 ,Γ为最小函数间隔,即:
,Γ为最小函数间隔,即:
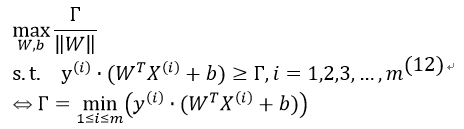
上式能够保证找到的超平面距离两个分类的数据点的集合的最小集合间隔相同。当W固定时,这时一个正样本到这个平面的距离和一个负样本到这个平面的距离之和的最小值也固定。对于相同的W、不同的b的超平面,其是互相平行的。不同的b会导致平面保持相同的“斜率”平移。假设这个平面从正负样本的正中间往正样本方向偏离一小段距离,那么可能是到正样本的最小距离变小,到负样本的最小距离变大,注意到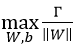 是将最小间隔最大化,所以这个最小值还存在优化空间,并不是我们最后的最优的结果,所以从这个角度看,直线位于正中间是最优的。
是将最小间隔最大化,所以这个最小值还存在优化空间,并不是我们最后的最优的结果,所以从这个角度看,直线位于正中间是最优的。
3、目标化简
为了简化式11,我们可以令Γ=1,即将最小函数间隔设为1。设z为实际的函数最小间隔值,两边同除以z值,则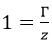 ,则相当于对WT、b进行了缩放,但对超平面的确定并没有影响。该操作的实际意义是同时缩放WT、b让距离超平面最近的那些样本点的函数间隔为1(即支持向量),这样调整后,不仅对原来的优化问题没有影响,而且还能简化计算。
,则相当于对WT、b进行了缩放,但对超平面的确定并没有影响。该操作的实际意义是同时缩放WT、b让距离超平面最近的那些样本点的函数间隔为1(即支持向量),这样调整后,不仅对原来的优化问题没有影响,而且还能简化计算。
因此优化问题变为:
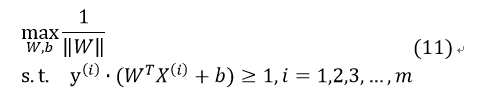
既然距离超平面最近的那些数据点到超平面的距离为1,那么其他远离超平面的点到超平面的函数间隔>1。
我们还可以将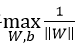 转换为求解
转换为求解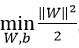 ,两者等价,且便于之后的推导。因此,我们得到SVM的目标函数的基本公式:
,两者等价,且便于之后的推导。因此,我们得到SVM的目标函数的基本公式:
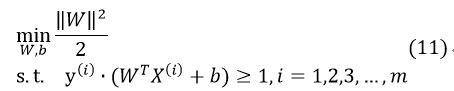
此时问题转换为凸优化问题(目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题<QP问题>)。
4、拉格朗日乘子法
优化问题
在优化式11之前,需要先对优化问题做梳理。
1、无约束优化问题
该问题如下:
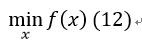
通过求导,使得导数为0的即为局部最小值。
2、等式约束优化问题

引入拉格朗日乘子:

拉格朗日条件如下:
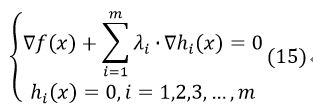
即通过对L(x,λi)分别对x,λi求偏导,并使得偏导数为0。
3、不等式约束优化问题
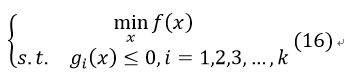
引入KKT乘子μi:

其解需要满足KKT条件:
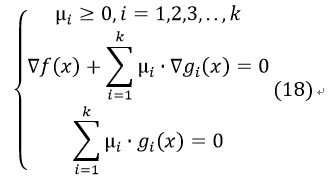
若为最大化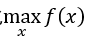 ,则条件2变为:
,则条件2变为:
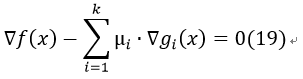
4、最一般的优化问题
首先要介绍一般的最优化问题,即既有等式约束、又有不等式约束。
考虑以下问题:
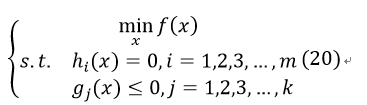
引入拉格朗日乘子(针对等式约束)λi和KKT乘子(针对不等式约束)μj,得到广义拉格朗日函数:

其中:
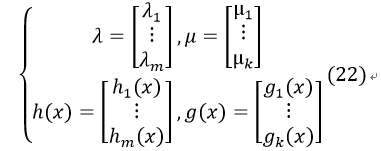
该函数的约束条件如下:
1、 Stationarity——梯度要求

若为最大化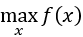 ,则条件变为:
,则条件变为:
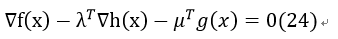
2、 Primal feasibility——原始约束条件
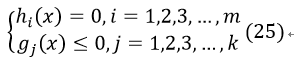
3、 Dual feasibility
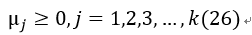
4、 Complementary slackness(互补松弛条件)
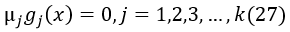
SVM目标函数转化
对于式11,我们先对不等式进行转换:
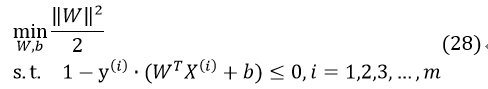
引入KKT乘子αi,得到拉格朗日函数:
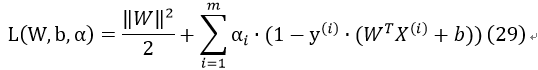
其需要满足的KKT条件为:
1、梯度条件
分别对W,b求偏导:

2、KKT乘子需满足条件:
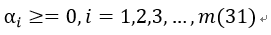
3、松弛互补条件:
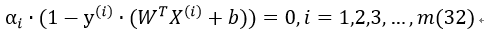
从上述条件可知:
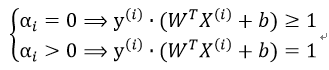
即对应KKT乘子为0的数据点肯定为支持向量。
5、转化对偶形式
原问题和对偶问题
介绍
假设原问题如式20中一般的优化问题所示,定义:
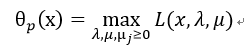

现在再定义:
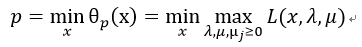
则上式与式20等价。于是我们就把原始的约束问题表示为广义拉格朗日函数的极小极大问题。其中p为最优值。
然后我们介绍其对偶问题(颠倒求极小和极大的顺序),定义:
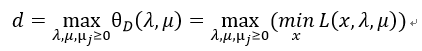
d为其最优值。现在的问题是d与p之间存在什么关系?
弱对偶定理
显然,对任意的x,λ,μ:
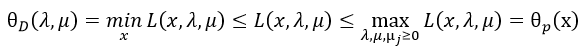
对偶问题与原问题的最优解相等的充要条件
对于原始问题和对偶问题,假设函数f(x)和gj(x)是凸函数, hi(x)是仿射函数(最高次数为1的多项式函数。常数项为零的仿射函数称为线性函数,可理解为形如y=ax+b的函数),且不等式约束gj(x)是严格可行的(严格可行即存在x,对于所有的i,都有gj(x)≤0),那么,x,λ,μ既是原始问题的最优解也是对偶问题的最优解的充要条件是:x,λ,μ满足KKT条件。
SVM目标函数转对偶
原SVM问题转化为极小极大形式(等效形式):
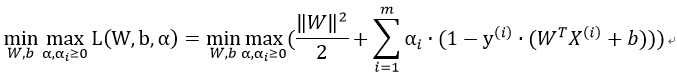
其对偶形式为:
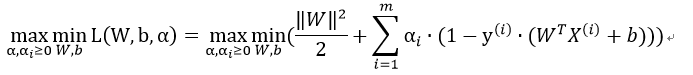
因为其满足KKT条件,故:

因此我们先求解:
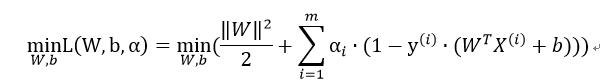
要使得上式最小,通过对W,b求偏导,令偏导数最小,得到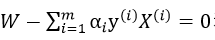 和
和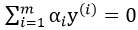 。再将其代入上式得:
。再将其代入上式得:
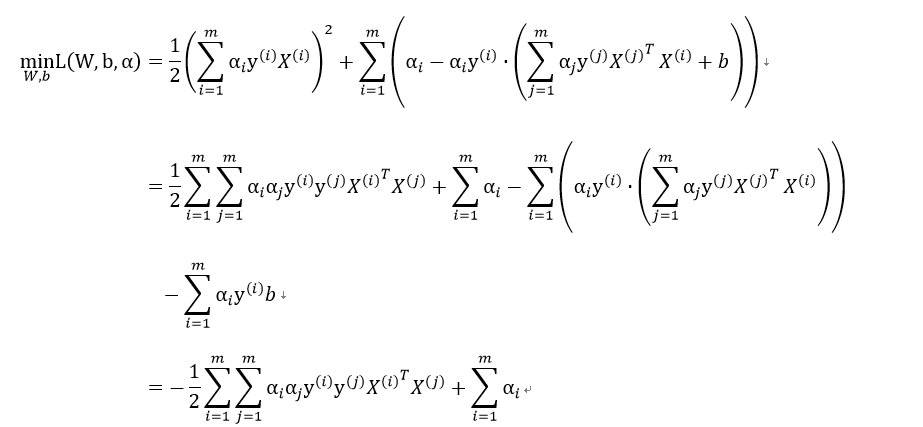
注意:
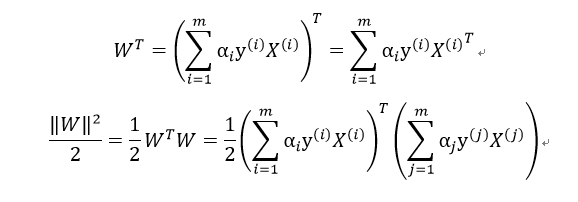
因此最后的优化目标函数为:
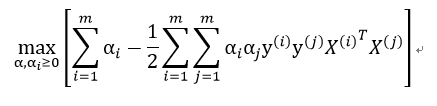
约束条件为:
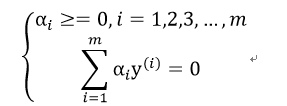
当训练得到α之后,由于:
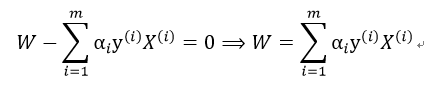
由上式可以计算得到W,之后通过下式计算b:
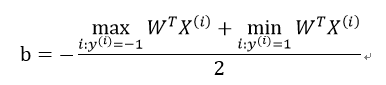
或者通过支持向量来计算:

6、异常值outlier处理
当数据线性不可分时,或存在异常值outlier(原本为负样例的数据点跑到正样例中),此时若仍要寻找一个超平面把两类的数据点完全分开,可能会使超平面倾斜、最小间隔变小,甚至找不到这样一个超平面。而这些异常值可能本就属于错误数据或噪声,没有必要使其一定划分到正确的边界两侧(采取硬间隔分类)。
折中的方案是允许部分数据点在一定程度上位于间隔边界内部,即其函数间隔小于1.
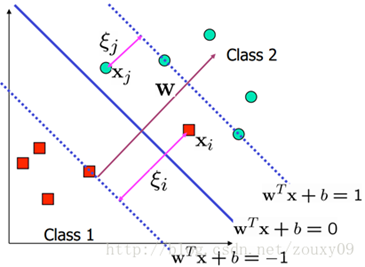
于是我们引入松弛因子ξi,表示允许样本点在超平面的相对平移量:
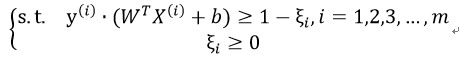
因为松弛因子是非负的,因此最终的结果是要求间隔可以比1小。但是当某些点出现这种间隔比1小的情况时(这些点也叫离群点),意味着我们放弃了对这些点的精确分类,而这对我们的分类器来说是种损失。但是放弃这些点也带来了好处,那就是使分类面不必向这些点的方向移动,因而可以得到更大的几何间隔(在低维空间看来,分类边界也更平滑)。
但是放弃我们需要平衡损失。原始的目标函数为:
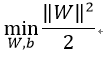
而由忽略异常值造成的损失会使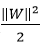 增大,我们需要加上损失量:
增大,我们需要加上损失量:
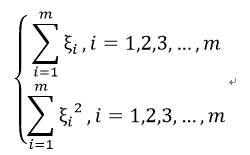
选择第一种的称为一阶软间隔分类器,第二种为二阶软间隔分类器,两者没有太大的区别。
再把损失加入目标函数中,需要一个惩罚因子C,表示离群点的权重,C越大表明离群点对目标函数影响越大,也就是越不希望看到离群点。这时候,间隔也会很小。我们采用第一种分类器:
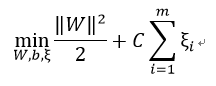
最后原模型变为:
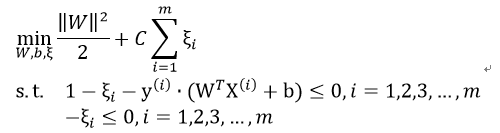
这样,经过同样的引入KKT乘子αi和βi:

转化对偶形式:
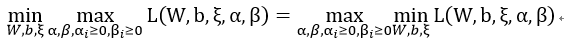
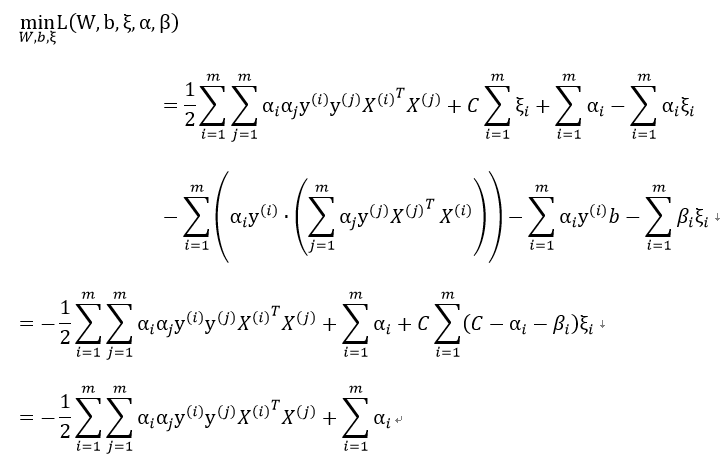
因为:
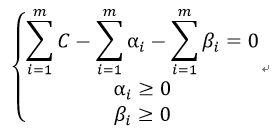
我们可以得到αi新的约束条件,并约去βi:

因此,最后的优化目标为:
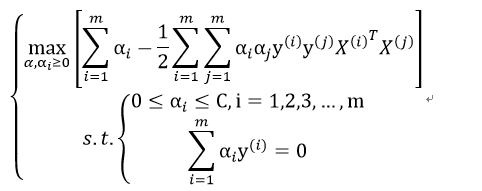
从上述条件结合其KKT条件可知:
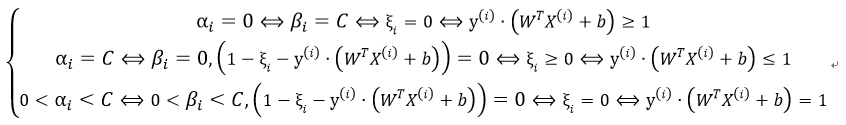
所以离群点的KKT乘子为C,位于间隔边界外的点的KKT乘子为0,属于支持向量的点的KKT乘子范围在(0,C)之间。但是在边界上的点其可能是支持向量、离群点或其他点。
7、通过SMO算法优化α
简介
根据我们最后的优化目标:
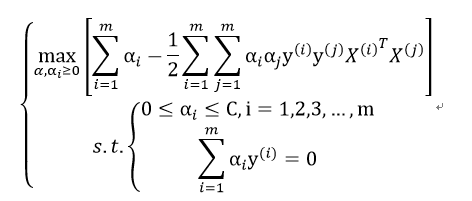
我们需要求出m个符合条件的最优的αi。
为了求解m个参数,如果不存在约束条件,可以通过坐标上升法,即固定其中其他参数,优化目标转变为关于一个变量的极值问题,可通过求导计算得到当前最优值(极大或极小)下该选定参数的取值。之后通过迭代多次以达到优化目的。
然而,在该问题中,存在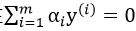 这一约束,如果选取一个αi且固定其他α,则当前选取的αi在该约束条件下已经是固定值。因此我们可以选取2个变量,固定其余m-2个变量,转化为一个二元函数求解。
这一约束,如果选取一个αi且固定其他α,则当前选取的αi在该约束条件下已经是固定值。因此我们可以选取2个变量,固定其余m-2个变量,转化为一个二元函数求解。
而SMO算法的核心在于将一个大的优化问题转化为多个小优化问题来求解。即每次寻找2个αi,我们记做α1和α2,对这两个αi进行优化。
具体步骤为:
1、通过启发式方法寻找一对α1、α2。(有的提出简化版SMO算法,即通过两层遍历全部数据集并限制最大迭代次数来确定α1、α2)。
2、固定除了α1、α2 之外的其他参数,确定目标函数取极值下的α1,α2 可通过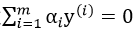 由α1表示得到。
由α1表示得到。
推导过程
转为二元函数
为推导方便,设:
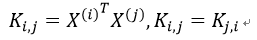
Ki,j表示列向量X(i) 和X(j)的点积(数量积).
假设已经有选好的2个变量,记为α1、α2 ,并把优化目标函数记为W(α1,α2 ),那么(注意 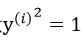 ):
):
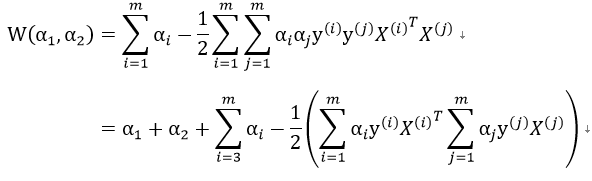
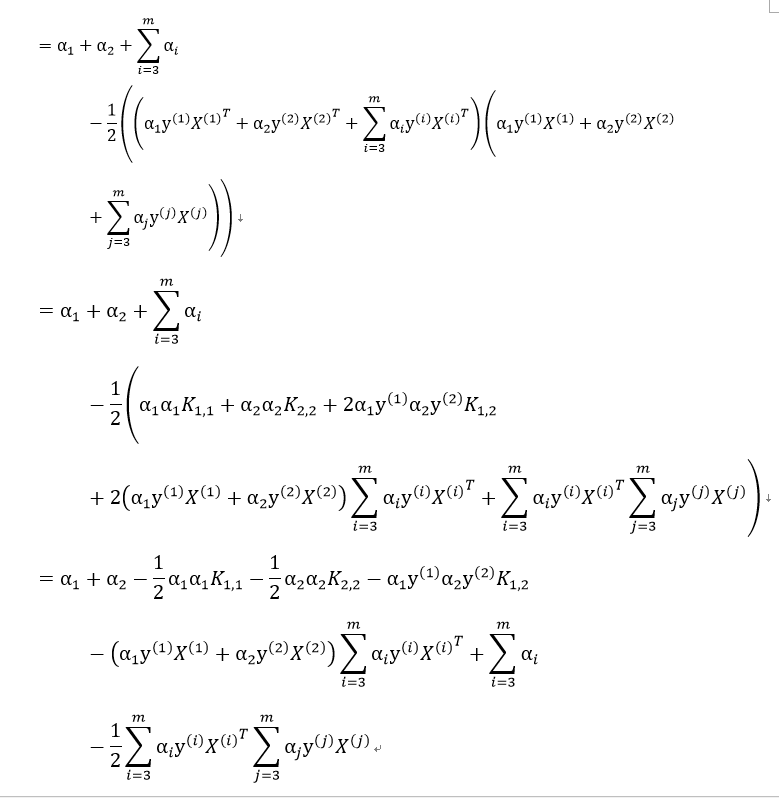
我们对上式取负,则优化最大值问题变为优化最小值问题:
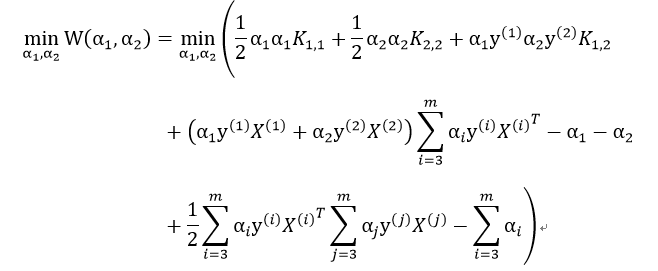
现在,我们的优化目标转变为一个二元函数。
由于等式约束,我们得到下式:
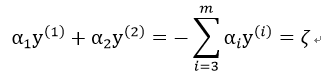
其中ζ为常量(因为此时我们已固定除α1,α2之外的参数)。
两边同乘以y(1):
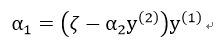
对α2求导
把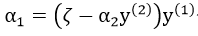 代入得到的二元函数中:
代入得到的二元函数中:
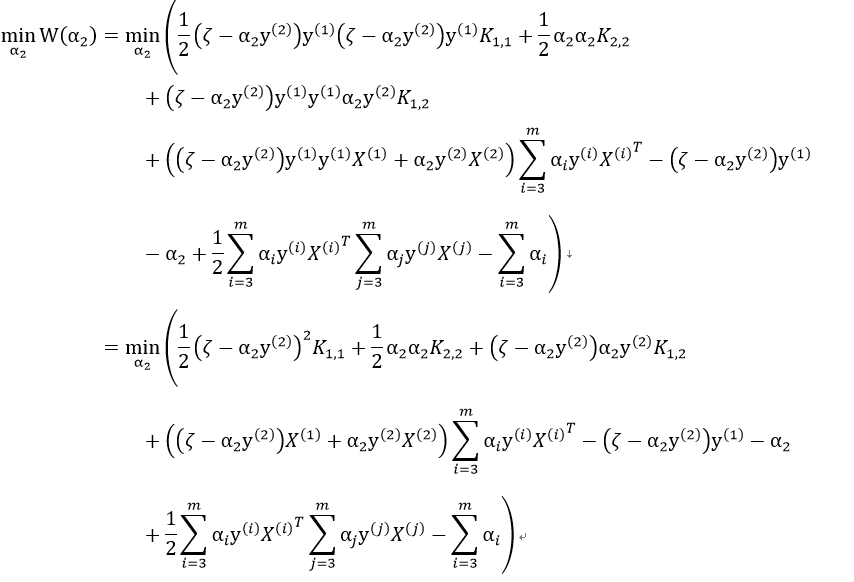
其中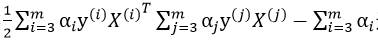 这最后两项为常数项,记为 yc:
这最后两项为常数项,记为 yc:
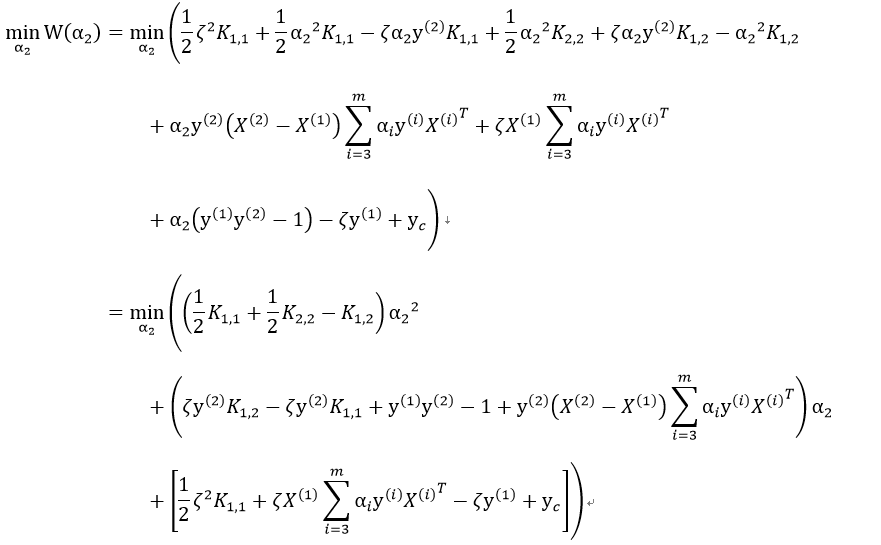
W(α2)对α2求导,并令导函数为0,得:
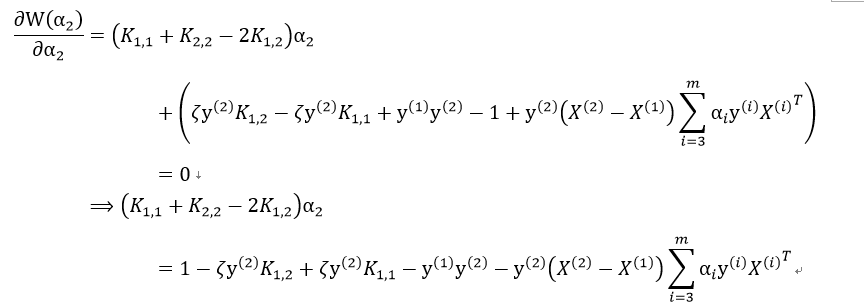
α1,α2迭代关系式
假设上一次迭代的α1,α2记做α1*,α2*,则有:
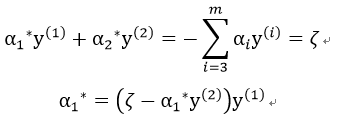
于是我们得到新旧值之间的联系。将其代入到α2导函数得到的等式中,得到:
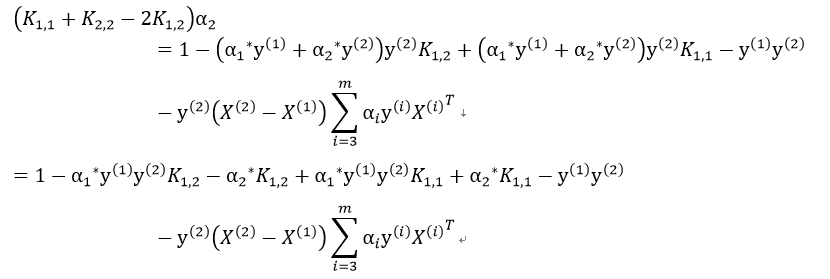
同时,由于:
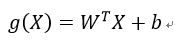
我们设:
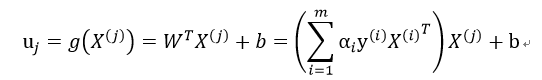
因此:

注意此处的μ1,μ2为使用α1*,α2*计算得出。
带回原式,得到:
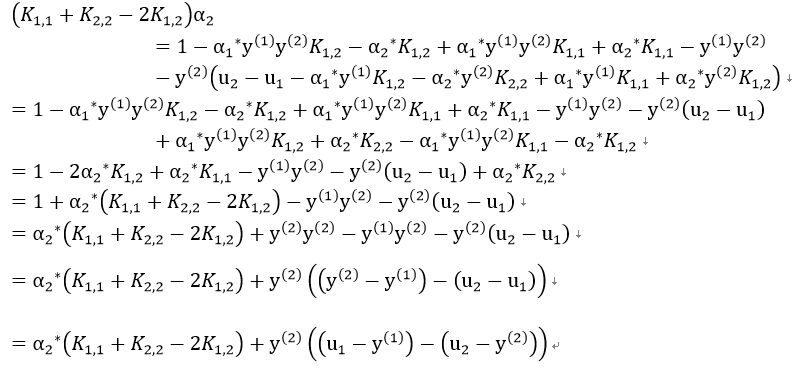
我们记误差值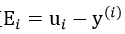 ,则有:
,则有:
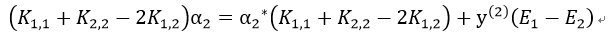
于是我们便可以得到α2的迭代关系式:
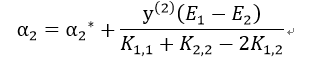
则α1的迭代关系式为:

此时,我们已经找到使得导函数为0的α系数的迭代关系式,但是,这仅仅是通过导函数为0得到的,也就是说,这仅仅是极值点,不一定为最值点,有以下几个问题:
1、取极值点的α位于定义域之外
2、最值点位于定义域边界
当然,在约束问题中,所谓的定义域即取值的可行域。
同时,在迭代关系式中,分母为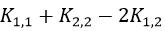 ,这也刚好为W(α2)中平方项的系数。因此也需要对其进行讨论。
,这也刚好为W(α2)中平方项的系数。因此也需要对其进行讨论。
判断可行域
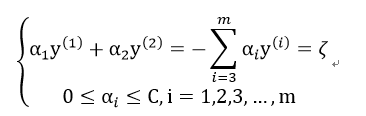
上面2式共同决定了α2的可行域:




因此,我们综合上述情况,得知:

判断系数:K1,1+K2,2-2K1,2
由前面推导过程可知,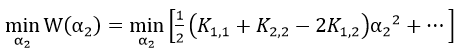 ,而令导数为0,更新α2的值需要在K1,1+K2,2-2K1,2为正的情况下。
,而令导数为0,更新α2的值需要在K1,1+K2,2-2K1,2为正的情况下。
此处我们应当讨论K1,1+K2,2-2K1,2不为正的情况。
1)K1,1+K2,2-2K1,2=0
此时W(α2)转变为一次函数,更新时不用求导,只需看边界值L,H,选取较小的那一个。而对于α1,则通过表达式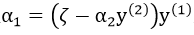 来分析。
来分析。
2)K1,1+K2,2-2K1,2<0
此时二次函数开口向下,最小值也是在可行域的边界处取到。此时开口向下,当极值点在区间内时,最小值只能在端点处取,因为极值点处是最大的。而当极值点在区间外时,区间内一定是单调的,此时最小值也只能在端点处取。
如何根据边界值L,H计算对应的函数值呢?
分别用α2的边界值L,H代入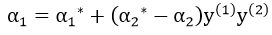 ,得到α1的两个”边界值” L',H',再把这两对取值代入W(α1,α2)中,选择值较小的进行更新。
,得到α1的两个”边界值” L',H',再把这两对取值代入W(α1,α2)中,选择值较小的进行更新。
计算b
每一轮更新α1,α2的同时,需要对b也要进行更新,因为b涉及到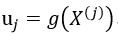 、误差值
、误差值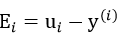 的计算。
的计算。
设已经更新结束的α1,α2记为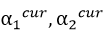 。
。
1) 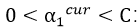
此时我们可以推出:
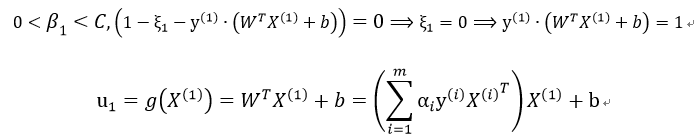
由上述两式可得:

由此知:
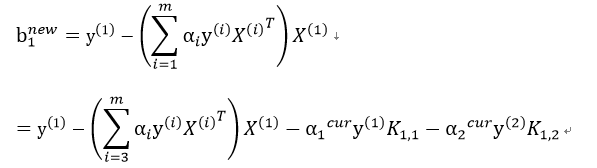
因为:
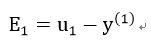
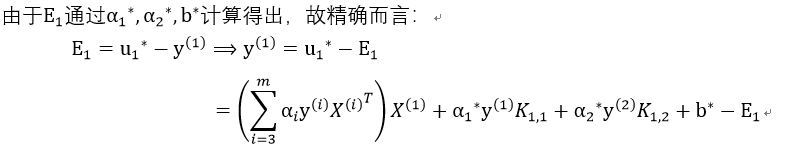
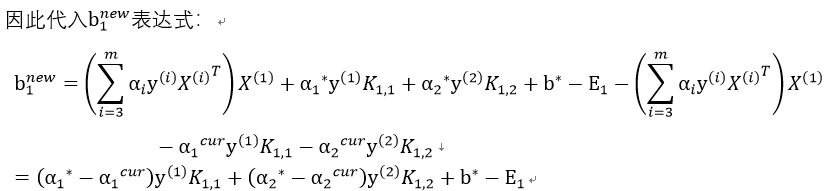
2) 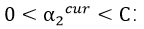
经过和上步相似的推导过程:
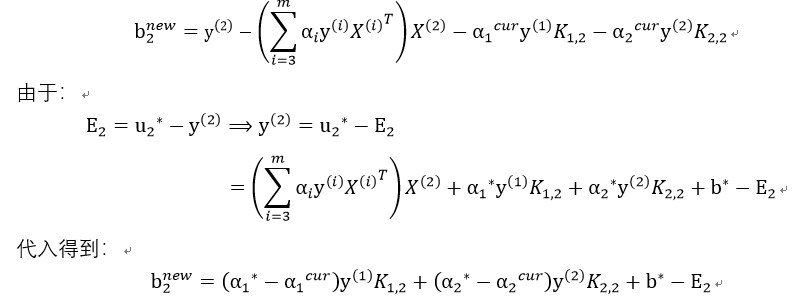

α1、α2的选择
之间所有的推导都基于α1、α2已经选取的情况下,那么我们现在讨论如何选取合适的α1、α2,即从m个α值选取两个α值。
在John C. Platt的论文《Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines》中采用一种启发式方法:每次选择KKT乘子的时候,优先选择样本0<αi<C的αi作优化(论文中称为无界样例),因为在界上(αi=0或αi=C)的样例对应的系数αi一般不会更改。
ⅰ、外循环——寻找第一个α
此处在遍历整个样本数据集和遍历满足0<αi<C的数据集交替。
①遍历一遍整个数据集,对存在下述情况的αi进行优化(即违反了KKT条件)
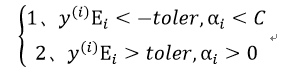
其中toler表示error-tolerant rate,即容错率,也就是 的最小误差,为人为规定,允许存在一定的误差。
我们之前从约束条件和KKT条件得知:
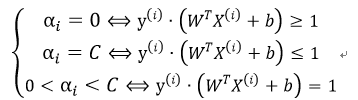
我们应当选择的所有αi及其对应的y(i)、X(i)应当都满足上述条件。因此,我们需要优化的αi为不满足上述条件的情况:

由于允许一定的误差,故基本不会有数据点使得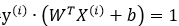 ,因此不予考虑。
,因此不予考虑。
我们对这两个条件进行分析:
1)对第一个条件:
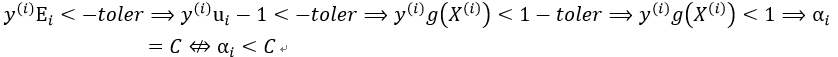
由此违反KKT条件。
2)对第二个条件:

由此违反KKT条件。
②在上面对整个数据集遍历一遍后,选择那些参数0<αi<C的子集,检查其是否违反KKT条件并进行优化。
③遍历完子集后,重新开始①②,不断在整个样本数据集和遍历满足0<αi<C的数据集交替,直到在执行①和②时没有任何修改即所有的αi都符合KKT条件则结束。
ⅱ、内循环——寻找第二个α
当我们选取了第一个α后,为了能快速收敛,希望第二个选取的α在优化后能有较大的变化。
而我们得知,α2的迭代关系式为 ,则新的α2与旧值之间的变化依赖于|E1-E2|。
,则新的α2与旧值之间的变化依赖于|E1-E2|。
①先在0<αi<C的集合中选择能最大化|E1-E2|的α2。
②如果不存在(符合0<αi<C的集合为空),则在整个样本数据集寻找。(通常随机选择一个)
③否则重新选取第一个α。
3、核函数的应用
对于非线性的情况,SVM 的处理方法是选择一个核函数,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。
此外,因为训练样例一般是不会独立出现的,它们总是以成对样例的内积形式出现,而用对偶形式表示学习器的优势在为在该表示中可调参数的个数不依赖输入特征的个数,通过使用恰当的核函数来替代内积,可以隐式得将非线性的训练数据映射到高维空间,而不增加可调参数的个数(当然,前提是核函数能够计算对应着两个输入特征向量的内积)。
核函数
根据模式识别理论,低维空间线性不可分的模式通过非线性映射到高维特征空间则可能实现线性可分,但是如果直接采用这种技术在高维空间进行分类或回归,则存在确定非线性映射函数的形式和参数、特征空间维数等问题,而最大的障碍则是在高维特征空间运算时存在的“维数灾难”(随着维数的增加,计算量呈指数倍增长的一种现象)。采用核函数技术可以有效地解决这样问题。

下面将举个例子。
假如x,y∈R(3):
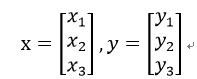
存在非线性映射:
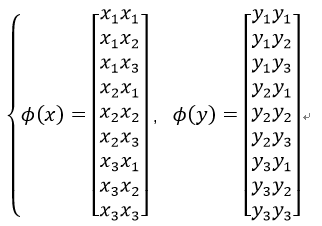
则在特征空间的内积:

而其核函数记为:

如果设维度为n,直接用非线性映射计算内积将达到n2的复杂度;采用核函数,则可在n的复杂度完成计算。
也就是说,我们通过核函数,用低维的计算量得到了高维的结果,没有增加计算复杂度的同时,得到了性质更好的高维投影。
Mercer定理
任何半正定的函数都可以作为核函数。
对于给定的任意向量集合:
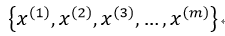
任意两个向量的核函数组成的矩阵为核矩阵:

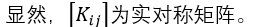
对于任意的列向量z,根据内积的非负性,有:

因此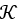 如果是核函数,那么对于任意的样本集合,得到的核矩阵为半正定矩阵。
如果是核函数,那么对于任意的样本集合,得到的核矩阵为半正定矩阵。
mercer定理不是核函数必要条件,只是一个充分条件,即还有不满足mercer定理的函数也可以是核函数。常见的核函数有高斯核,多项式核等等,在这些常见核的基础上,通过核函数的性质(如对称性等)可以进一步构造出新的核函数。
常见核函数
1)线性核函数(Linear Kernel)
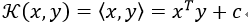
使用线性核的核算法通常等价于它们的非核函数
2) 多项式核函数(Polynomial Kernel)
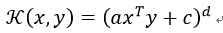
多项式核是一个非平稳的核。多项式内核非常适合所有训练数据被规范化的问题。可调参数是斜率a,常数项c和多项式指数d。
3) 高斯核函数(Gaussian Kernel)
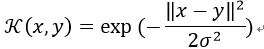
或者,其也能使用:
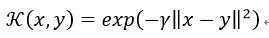
是一种径向基核函数(Radial Basis Function)。该核函数被广泛使用,但是这个核函数的性能对参数 十分敏感。如果过高,指数会表现得几乎是线性的,高维的投影会开始失去它的非线性能量。另一方面,如果被低估,该函数将缺乏正则化,且决策边界对训练数据中的噪声非常敏感。高斯核函数也有了很多的变种,如指数核,拉普拉斯核等。
4) 双曲正切Sigmoid核函数
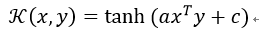
注:
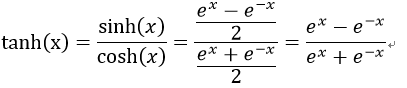
双曲切核也被称为Sigmoid内核和多层感知器(MLP)内核。Sigmoid内核来自于神经网络领域,在该领域中双极性Sigmoid函数常被用作人工神经元的激活函数。
值得注意的是,使用sigmoid内核函数的SVM模型等价于一个两层的感知器神经网络。由于神经网络理论的起源,这种内核在支持向量机方面相当流行。此外,尽管它只是有条件的肯定,但它在实践中被发现表现良好。
在sigmoid内核中有两个可调参数,即斜率a和截距常数c, a的一个通常值是1/n,其中n为数据维数。关于sigmoid核函数的更详细的研究可以在Hsuan-Tien和Chih-Jen的作品中找到。
5)指数核函数(Exponential Kernel)
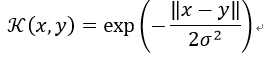
指数核函数就是高斯核函数的变种,它仅仅是将向量之间的L2距离调整为L1距离,这样改动会对参数的依赖性降低,但是适用范围相对狭窄。它也是一个径向基函数核。
6)拉普拉斯核函数(Laplacian Kernel)
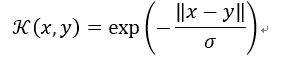
拉普拉斯核完全等价于指数核,唯一的区别在于前者对参数的敏感性降低,也是一种径向基核函数。
7) ANOVA Kernel
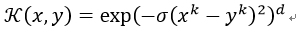
ANOVA 核也属于径向基核函数一族,其适用于多维回归问题。
8) 二次有理核(Rational Quadratic Kernel)
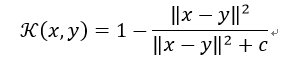
二次有理核函数在计算上比高斯核小,在使用高斯函数时,可以作为一种替代方法。这个核函数作用域虽广,但是对参数十分敏感,慎用。
9)多元二次核(Multiquadric Kernel)
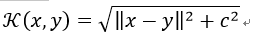
多元二次核可以替代二次有理核,和Sigmoid内核一样,它也是一个非正定内核。
10) 逆多元二次核(Inverse Multiquadric Kernel)

基于这个核函数的算法,不会遇到核相关矩阵奇异的情况。与高斯核一样,它的结果是一个具有全秩的核矩阵(Micchelli, 1986),从而形成一个无限维的特征空间。
11)Circular Kernel
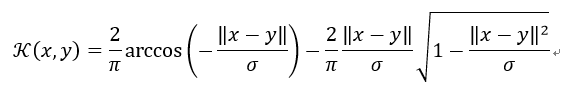
圆形核来自于统计透视图。它是各向同性静止核的一个例子,在 中是正定的。
12) Spherical Kernel
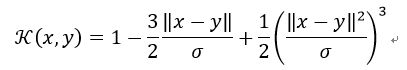
球形核与圆形核相似,但在R3中正定。
13) Wave Kernel
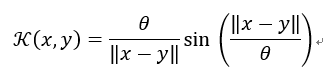
适用于语音处理场景。为对称的正半定。
14)Power Kernel
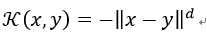
也称为(未纠正的)三角核(triangular kernel)。它是一个标量不变核(Sahbi和Fleuret, 2004)的例子,而且也只是有条件的正定。
15)对数核函数(Log Kernel)
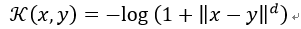
对于图像来说,对数核似乎特别有趣,但它只是有条件的正定。
16) 样条核(Spline Kernel)
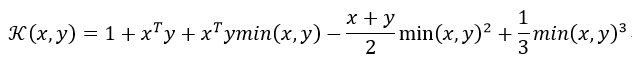
其实际是指:
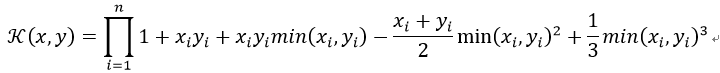
样条核是由Gunn(1998)的论文所导出的一个分段三次多项式。
17) b样条核(B-Spline (Radial Basis Function) Kernel)
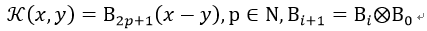
在Bart Hamers的论文中,其为:
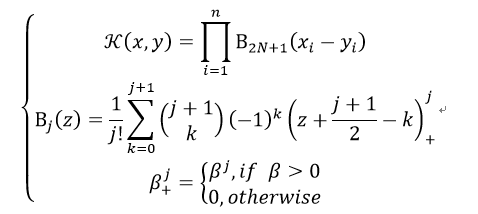
18) Bessel Kernel
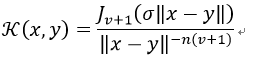
其中J是第一种贝塞尔函数(Bessel function of first kind)。
然而,在Kernlab的R文档中,Bessel核被认为是:

贝塞尔核在分数平滑的函数空间理论中众所周知.
19)柯西核函数(Cauchy Kernel)
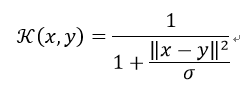
与柯西分布相似,函数曲线上有一个长长的尾巴,是一种长尾核,说明这个核函数的定义域很广泛,言外之意,其可应用于原始维度很高的数据上。
20)卡方核函数(Chi-Square Kernel)
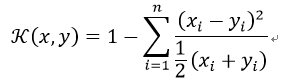
卡方核来自卡方分布。
它存在着如下变种:
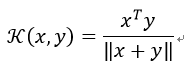
这个核函数基于的特征不能够带有赋值,否则性能会急剧下降,如果特征有负数,那么就用下面这个形式:

21)直方图交叉核(Histogram Intersection Kernel)
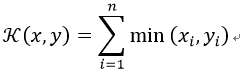
在图像分类里面经常用到,比如说人脸识别,适用于图像的直方图特征,例如extended LBP。
22) 广义直方图交叉核(Generalized Histogram Intersection kernel)

广义直方图交叉核是基于图像分类的直方图交叉核构建的,但适用于更大的上下文环境。
23)Generalized T-Student Kernel
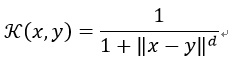
属于mercer核,具有一个正半定核矩阵。
24)贝叶斯核(Bayesian Kernel)
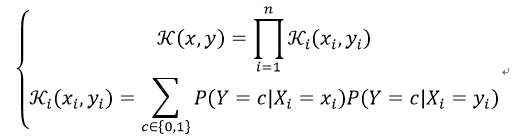
贝叶斯核取决于被建模的问题。
25)小波核(Wavelet kernel)
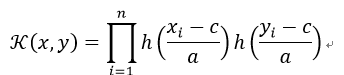
其来源于小波理论。其中a和c分别是小波扩张和平移系数。
这个内核的平移不变版本(translation-invariant version)可以是:
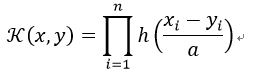
h(x)中表示母波函数。在李章、周伟达和李诚的论文中,作者提出了一个可能的h(x):

它们被证明为admissible kernel function.
26)复合核函数
复合核函数也叫混合核函数,是将两种或两种以上的核函数放在一起使用,形成一种新的核函数。
如何选择核函数
如果特征的数量大到和样本数量差不多,则选用LR或者线性核的SVM;
如果特征的数量小,样本的数量正常,则选用SVM+高斯核函数;
如果特征的数量小,而样本的数量很大,则需要手工添加一些特征从而变成第一种情况。

SVM应用
在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。如图所示,一堆数据在二维空间无法划分,从而映射到三维空间里划分:
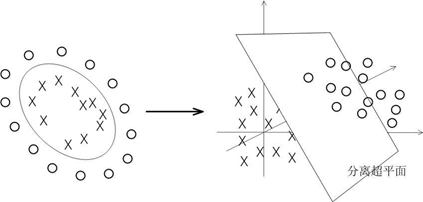
而在我们遇到核函数之前,如果用原始的方法,那么在用线性学习器学习一个非线性关系,需要选择一个非线性特征集,并且将数据写成新的表达形式,这等价于应用一个固定的非线性映射,将数据映射到特征空间,在特征空间中使用线性学习器,因此,考虑的假设集是这种类型的函数:
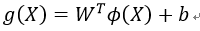
 是从输入空间到某个特征空间的映射,这意味着建立非线性学习器分为两步:
是从输入空间到某个特征空间的映射,这意味着建立非线性学习器分为两步:
1、首先使用一个非线性映射将数据变换到一个特征空间F;
2、然后在特征空间使用线性学习器分类。
如果用内积表示,则:
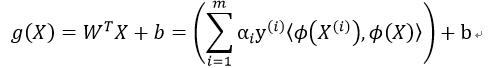
核函数能够让其在特征空间直接计算内积 ,而且无需知道非线性映射的显式表达式。因此目标函数转化后的对偶形式应当改为:
,而且无需知道非线性映射的显式表达式。因此目标函数转化后的对偶形式应当改为:

4、利用结果预测
未使用核函数
利用算出的W或α和b来预测:
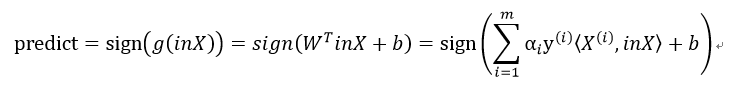
使用核函数
利用算出的α和b来计算:
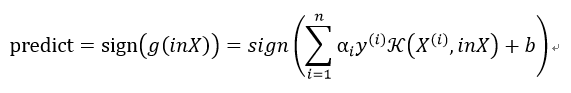
出处:http://www.cnblogs.com/ivan-count/
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号