决策树

一、概念

决策树模型是一种描述对实例进行分类的树形结构。决策树由结点和有向边组成。结点有两种类型：内部节点和叶节点，内部节点表示一个特征或属性，叶节点表示一个类别。

分类的时候，从根节点开始，对实例的某一个特征进行测试，根据测试结果，将实例分配到其子结点；此时，每一个子结点对应着该特征的一个取值。如此递归向下移动，直至达到叶结点，最后将实例分配到叶结点的类别中。

决策树是一种贪心算法，要在给定时间内作出最佳选择，但并不关心能否达到全局最优。

以下为各决策树算法比较：

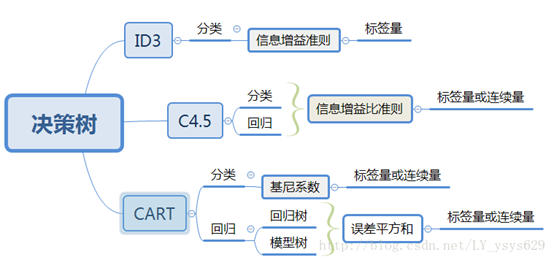
二、ID3算法

构造决策树即为从上到下构造结点特征的过程，当前结点应当选取为对所需划分的数据集起决定性作用的特征。

香农熵

划分数据集应当遵循的原则为：将无序的数据变得更加有序。

香农熵（简称熵）被用来度量集合的信息的有序或无序。

1、信息的定义

如果待分类的事物可能划分在多个分类中，则符号x_i的信息定义为：

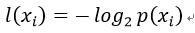
其中p(x_i)是选择该分类的概率。

2、香农熵的计算

为了计算熵，需要计算所有可能值包含的信息期望值：

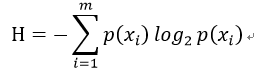
其中m表示分类的数目。

熵越高，则表明混合的数据越多,纯度越低，有序程度越低，分类效果越差。

基尼不纯度

基尼不纯度是指将来自集合的某种结果随机应用于某一数据项的预期误差率：

基尼不纯度越小，纯度越高，集合的有序程度越高，分类的效果越好。

基尼不纯度为 0 时，表示集合类别一致；基尼不纯度最高（纯度最低）时，p(x_i)=1/m。

信息增益

信息增益表现为熵的减少或数据无序度的减少：

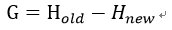
当采用基尼不纯度时：

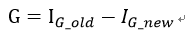
得到最优特征

①计算当前数据集的香农熵，记为H_old(使用基尼不纯度度量无序程度时，记为I_{G_old})，并记录当前数据集的样本数为n，样本类别总数为m。

②遍历所有特征，设当前特征为i。

③遍历特征i的所有属性取值，记当前取值为j，不同取值总数为γ，设特征i取值为j的子集样本数为n_j，则以特征i划分的信息增益为：

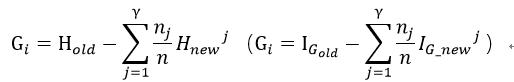
其中H_new^j为对应特征i取值为j的子集的香农熵(I_{G_new}^j为对应特征i取值为j的子集的基尼不纯度)。

④选取G_i最大的特征作为当前结点的特征。

构建决策树

首先我们将得到原始数据集，然后基于最好的特征划分数据集，此时将会根据该特征的取值不同而有多个分支。第一次划分后，数据将被传递到树分支的下一个结点，依照同样的策略继续进行划分。

按照上述思路，我们可以递归地得到一棵决策树，递归结束的条件是：遍历完所有划分数据集的特征，或每个分支下的所有样本都具有相同的类别。

如果当我们遍历完所有的特征后，该分支下的样本仍属于不同的类别，通常采用多数表决的方法，即以其中最多样本所隶属的类别作为该叶结点的取值。

三、C4.5算法

四、CART算法

ID3每次会选取当前最佳的特征来分割数据，并按照该特征的所有可能取值来切分，而在按照某特征切分之后，该特征在之后的ID3算法执行过程中不再起作用，有观点认为该方法切分过于迅速。

CART算法采用二元切分法，每次把数据切成2份。对于离散型数据，如果数据的某特征值等于切分所要求的值，则这些数据进入左子树，否则进入右子树；对于连续型数据，则可以采用回归方法，如果某特征值大于给定值则进入左子树，否则进入右子树。

1、分类决策树

2、回归树

回归树将叶结点置为常数。即在每个叶结点利用训练数据的均值做预测。

1、找到最佳切分特征

初始化最大误差为INF。

①遍历所有特征（第一重循环）

②遍历其所有取值（第二重循环）

③按照当前的特征及其取值，将大于该值的样本归于一类，小于等于该值的样本为另一类，计算分为两类前后总平方误差的大小，如果切分后总平方误差之和小于切分前总平方误差之和，则更新记录值。

切分前总平方误差之和计算：

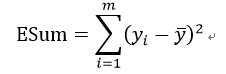
切分后总平方误差之和计算：

④所有特征遍历结束后，返回最佳切分特征和最佳阈值。

注意：如果当前数据集所有样本y取值只有一种情况，则为叶结点，返回叶结点常数取值（通常取y的平均值）。

2、预剪枝

可以人为指定最小误差下降值tolS以及切分的最小样本数tolN。

①如果ESum2与Esum之差小于tolS，则直接建立叶结点。

②如果切分后的两个子集有任意一个其样本数小于tolN，则直接建立叶结点。

3、后剪枝

该方法是基于已经构建出来的回归树和给定的测试数据进行的。

①遍历该回归树，如果存在任一子集为一棵树，则在该子集递归剪枝过程。

②如果当前结点的两个分支均为叶结点，则考虑合并：

先计算不合并的误差（设左右结点的值分别为Lmean、Rmean，当前测试子集在切分后左右两个子集大小分别为L_M、R_M）：

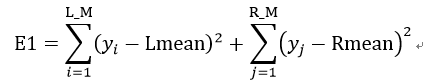
计算合并后的误差：

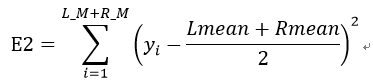
如果E2<E1，则将叶结点合并。

4、总流程

①找到最佳的遍历特征及其阈值。转②。

②如果该结点不能再分（返回特征为None），设为叶结点。否则转③

③如果可分，则继续切分，分别对左右子树调用①。

④对得到的回归树进行后剪枝。

注意：预剪枝可合并进寻找最佳特征及其阈值的过程中。

3、模型树

该方法将所有的叶结点设为分段线性函数，每个叶结点都是一个线性模型。其具有可解释性、高预测准确度。

不能再使用平方误差之和来衡量选取切分特征时的误差。对于给定的数据集，应当先用线性的模型对其进行拟合（比如先进行OLS线性回归），然后计算真实的目标值与模型预测值之间的差值。

同时，叶结点表示的线性模型的回归系数，而非常数。

其余步骤类似回归树。