朴素贝叶斯

1、概率

1、条件概率

对于条件概率，我们有：

表示在b已知的情况下（条件）发生a的概率。

2、概率的乘法法则

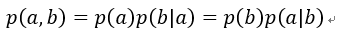
3、独立事件同时发生的概率

2、贝叶斯定理

贝叶斯定理联系先验概率和后验概率：

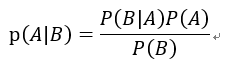
p(A|B)表示在B发生的情况下A发生的概率。

P(A)指先验概率；P(B|A)为似然函数，形式同条件概率；P(B)也为先验概率，可通过全概率公式计算得到；p(A|B)为后验概率。

不同：

①先验概率：事件发生前的预判概率。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率。

②后验概率：事件发生后求的反向条件概率。或者说，基于先验概率求得的反向条件概率。

③似然函数：是根据已知结果去推测固有性质的可能性（likelihood），是对固有性质的拟合程度。

在分类问题中，其可记做：

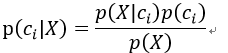
p(c_i|X)表示在给出数据X的条件下，其属于c_i的概率。 p(X|c_i)可称为类条件概率密度函数，p(X)可称为全概率密度，通过全概率公式得到：

基于贝叶斯准则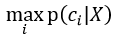，为数据X的分类。由于全概率对于所有的p(c_i|X)都相同，因此只需要比较分子的大小即可。

3、朴素贝叶斯假设-条件独立性假设

即X表示某个数据的n维特征，p(X|c_i)可以把X中的特征展开表示：

 

该假设为X的所有特征都相互独立，则：

对于离散型的特征，通常需要求其每一个取值的概率。而对于连续型特征，则将其离散化。

4、特征模型

约定：

样本数为m，c_i类别的样本数为m_i，总类别个数为C。

第i个样本的特征总数为α_i，其第j个特征取值情况有β_j种。

全部不同特征共A种，第j种特征x_j取值情况共B_j种，其第k种取值记为B_ik。所有特征不同取值情况总和记为B。

1、多项式模型

①适用数据类型

离散值。即对应的特征为离散的。比如性别（取值为男、女）、学历（小学、高中、本科、专科、硕士、博士、博士后）。

②模型介绍

该模型在一些书中也称为词袋模型。需要统计每个特征取值的样本数目。

在多项式模型中，通常含有平滑项σ，有：

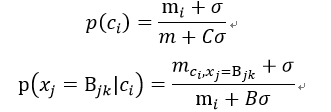
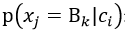表示在类别c_i中，特征x_j取值为B_k的概率； m_i表示类别为c_i的样本数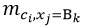； 表示类别为c_i的样本中，特征x_j取值为B_jk的样本数目；B表示所有特征的不同取值的总和；C为总类别个数。

σ=0时，表示不做平滑处理。

σ=1时，称为拉普拉斯平滑（Laplace平滑）。能够防止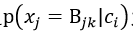为0而导致的后验概率为0的情况。

0<σ<1时，称为Lidstone平滑。

对于文本分类，则有：

m_i表示类别为c_i的词向量中所有出现单词的总和；表示类别为c_i的所有词向量中单词x_j出现的次数。

对于所预测的某个词向量，其可能并未包含所有词汇表的词，则只需将其出现的x_j来计算。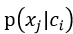

2、伯努利模型

 

①适用数据类型

离散值。

②模型介绍

该模型在有些书中也被称为词集模型。其与多项式模型类似，不过该模型中，每个特征取值只能为1或0，表示出现与否（对于文本分类而言，1表示某个单词出现在该文本中，0则表示没有出现），其全部特征取自全局。当然对于特征取值大于2的情况，需要自定义一定的阈值来判断0和1的取值情况。

3、高斯模型

①适用数据类型

连续型。比如身高等。

②模型介绍

高斯模型假设每一维特征都服从高斯分布（正态分布）：

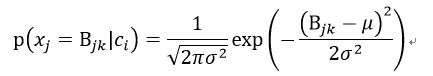
其中，μ表示类别为c_i、特征x_j的均值；

σ²为类别为c_i、特征x_j的方差。

B_jk是连续型变量x_j的某一个取值。

因此，只需对于样本数据得到每个类别中每个连续型特征的均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把某个预测数据的该连续性特征的值代入，算出某一点的密度函数的值。

5、处理技巧

有时会遇到下溢出问题，即过小，导致所有过小的数的乘积结果由于舍入为0。这时可以使用取对数的方法避免下溢出或浮点舍入导致的错误：

 

最后选取值最大的所对应类别即为预测类别。