威尔逊置信区间

由于正态区间对于小样本并不可靠，因而，1927年，美国数学家 Edwin Bidwell Wilson提出了一个修正公式，被称为“威尔逊区间”，很好地解决了小样本的准确性问题。

根据离散型随机变量的均值和方差定义：
μ=E(X)=0*(1-p)+1*p=p
σ=D(X)=(0-E(X))2(1-p)+(1-E(X))2p=p2(1-p)+(1-p)2p=p2-p3+p3-2p2+p=p-p2=p(1-p)
因此上面的威尔逊区间公式可以简写成：

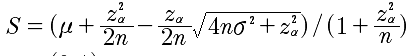
代码：

def wilson_score(pos, total, p_z=2.):
    """
    威尔逊得分计算函数
    参考：https://en.wikipedia.org/wiki/Binomial_proportion_confidence_interval
    :param pos: 正例数
    :param total: 总数
    :param p_z: 正太分布的分位数
    :return: 威尔逊得分
    """
    pos_rat = pos * 1. / total * 1.  # 正例比率
    score = (pos_rat + (np.square(p_z) / (2. * total))
             - ((p_z / (2. * total)) * np.sqrt(4. * total * (1. - pos_rat) * pos_rat + np.square(p_z)))) / \
            (1. + np.square(p_z) / total)
    return score

　　SQL实现代码：

#wilson_score
SELECT widget_id, ((positive + 1.9208) / (positive + negative) - 
                   1.96 * SQRT((positive * negative) / (positive + negative) + 0.9604) / 
                          (positive + negative)) / (1 + 3.8416 / (positive + negative)) 
       AS ci_lower_bound FROM widgets WHERE positive + negative > 0 
       ORDER BY ci_lower_bound DESC;
 
#
SELECT widget_id, (positive - negative) 
       AS net_positive_ratings FROM widgets ORDER BY net_positive_ratings DESC;
 
#
SELECT widget_id, positive / (positive + negative) 
       AS average_rating FROM widgets ORDER BY average_rating DESC;

　　excel实现代码：

=IFERROR((([@[Up Votes]] + 1.9208) / ([@[Up Votes]] + [@[Down Votes]]) - 1.96 * 
    SQRT(([@[Up Votes]] *  [@[Down Votes]]) / ([@[Up Votes]] +  [@[Down Votes]]) + 0.9604) / 
    ([@[Up Votes]] +  [@[Down Votes]])) / (1 + 3.8416 / ([@[Up Votes]] +  [@[Down Votes]])),0)

星级评价排名

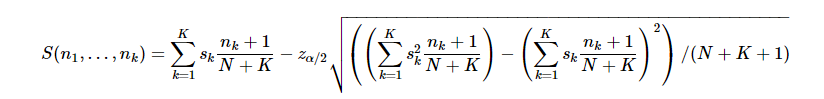
Reddit的话题排序算法叫做（thehot ranking），实现代码如下：

　　log(10, max{abs(up-down), 1}) + sign(up>down) * seconds / 45000

#Rewritten code from /r2/r2/lib/db/_sorts.pyx
 
from datetime import datetime, timedelta
from math import log
 
epoch = datetime(1970, 1, 1)
 
def epoch_seconds(date):
    """Returns the number of seconds from the epoch to date."""
    td = date - epoch
    return td.days * 86400 + td.seconds + (float(td.microseconds) / 1000000)
 
def score(ups, downs):
    return ups - downs
 
def hot(ups, downs, date):
    """The hot formula. Should match the equivalent function in postgres."""
    s = score(ups, downs)
    order = log(max(abs(s), 1), 10)
    sign = 1 if s > 0 else -1 if s < 0 else 0
    seconds = epoch_seconds(date) - 1134028003
    return round(order + sign * seconds / 45000, 7)